تصادفی

مدل های تعادل عمومی پویای تصادفی - DSGE

یک روش شناسی مدرن از تحلیل اقتصاد کلان می باشد.این مدل ها با ویژگی پویایی قابلیت تحلیل تعادلی متغیرهای کلان اقتصادی را فراهم می سازند. این مدل ها در تلاش برای تبیین پدیده های اقتصاد کلان همچون رشد اقتصادی، چرخه های تجاری، اثرات سیاست های پولی و مالی بر روی متغیرهای کلان و رفاه خانوارها هستند. مدل هایی که بدور از جهت گیری های مکتبی اقتصاد کلان از ابزارهای نیرومند ریاضیاتی چون نظریه کنترل بهینه و برنامه ریزی پویا به منظور ارائه تحلیل پویا و تعادلی از یک اقتصاد بکارگرفته می شوند. ویژگی بسیار مهم این مدل ها این است که واکنش متغیرهای اساسی کلان اقتصادی را در مقابل تغییر پارامترهای سیاستی را می توانند نشان دهند. این مدل ها پس از طرح انتقاد لوکاس در مورد عدم اعتماد به پیشنهادات سیاستی مدل های اقتصادسنجی سری زمانی خصوصا سیستم معادلات همزمان، بر پایه مفاهیم اساسی خرد اقتصادی، رفتار های بهینه مقید عاملان فردی اقتصادی و با تکیه بر پارامترهای اساسی چون ترجیحات زمانی افراد، نرخ استهلاک و قیود منابع  گسترش پیدا کردند. جهت برآورد مدل های تعادل عمومی روش های مختلف اقتصاد سنجی و کالیبراسیون پارامترها  ( کیدلند و پرسکات ، 1982) وجود دارد. از دیگر روش های موجود در زمینه تخمین تجربی و برآورد پارامترهای ساختاری مدل های DSGE  می توان به روش حداکثر راستنمایی کلاسیک ( سارجنت ، 1989) اشاره کرد. همچنین روشهایی بر پایه آمار بیزی و اقتصادسنجی بیزین در برخی از مطالعات اخیر تجربی دیده می شود. آمار ییزی با افزودن مفهوم توزیع پیشین داده ها به تابع راستنمایی و تشکیل توزیع پسین داده ها، بر پایه روش های شبیه سازی مونت کارلو (MCMC) و الگوریتم هایی چون Random-Walk Metropolis و Importance Sampling تجزیه و تحلیل تجربی مدل های تعادل عمومی را انجام می دهد. نرم افزار dynare نرم افزار نیرومندی جهت برآورد  مدل های DSGE است.

++C تولید اعداد تصادفی در

توليد اعداد تصادفی<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> يکی از کاربردهای اساسی کامپيوتر، استفاده از آن در کارهای شبيه سازی می باشد. در اينجا به بررسی نحوه توليد اعداد تصادفی می پردازيم. اعداد تصادفی در مسائل شبيه سازی کاربرد فراوانی دارند، به عنوان مثال شبيه سازی پرتاب سکه، پرتاب تاس و مسائلی از اين قبيل. برای توليد اعداد تصادفی زبان ++C تابعی با نام rand() را که در فايل کتابخانه ای stdlib.h قرار دارد، در اختيار ما گذاشته است. به عنوان مثال دستور زير : i = rand(); يک عدد تصادفی بين 1 تا 32767 را در متغير i قرار می دهد . تابعrand()اعداد را با احتمال مساوی در اين بازه انتخاب می کند پس شانس انتخاب هر عددی در اين بازه با اعداد ديگر برابر است. معمولاً بازه اعدادی که توسط تابع rand توليد می شود، با آنچه که مورد نياز ماست متفاوت می باشد. به عنوان مثال برای شبيه سازی پرتاب سکه به دو عدد تصادفی و برای تاس به شش عدد تصادفی نياز داريم. فرض کنيد که می خواهيد عدد 31250 را به عددی بين 1 تا 6 تبديل کنيد. چه راه کاری را در نظر می گيريد؟ راهی که برای اين تبديل وجود دارد استفاده از باقيمانده صحيح می باشد، همانطور که می دانيد باقيمانده صحيح تقسيم هر عددی بر 6 يکی از اعداد 0 تا 5 می باشد. پس با اضافه کردن 1 واحد به باقيمانده ، عددی بين 1 تا 6 خواهيم داشت. به عنوان مثال در کادر زير عددی بين 1 تا 32767 وارد کنيد و با کليک بر روی دکمه محاسبه خروجی ، نتيجه محاسبه را ببينيد :   Top of Form a=a%6+1= Bottom of Form حال اگر به جای متغير a ، تابع rand() را قرار دهيم عبارت rand()%6+1 عددی تصادفی بين 1 تا 6 به ما می دهد به طور کلی برای بدست آوردن عددی تصادفی در بازه [a,b] می توانيم از فرمول زير استفاده کنيم. rand()%(b-a+1)+a به عنوان مثال خروجی قطعه برنامه زير عدد صحيحی در بازه [20,100] می باشد. int a = 20 , b = 100; cout<< rand()%(b-a+1)+a; برنامه زير 20 عدد تصادفی بين 1 تا 6 را ايجاد می کند. که اين برنامه را می توان 20 بار پرتاب يک تاس در  نظر گرفت : #include #include   int main() {    for (int i = 1; i<= 20; i++ )     {      cout << rand() % 6 + 1<<"\t";        if ( i % 5 == 0 )         cout << endl;     }    return 0; } خروجی برنامه فوق به صورت زير می باشد : 5       5       3       5       5 2       4       2       5       5 5       3       2       2       1 5       1       4       6       4 يک بار ديگر برنامه فوق را اجرا کنيد و خروجی را مجدداً بررسی کنيد. خواهيد ديد خروجی دقيقاً همان اعداد قبلی می باشد. خروجی تابع rand() اعداد تصادفی می باشد ولی با اجرای دوباره برنامه همان اعداد مجدداً به همان ترتيب قبلی تکرار می شوند. اين تکرار يکی از قابليتهای تابع می باشد ودر اشکال زدايی ...

ادامه تکنیک های خلاقیت

تکنیک واژه تصادفی در این روش، ارتباطی اجباری بین موضوع مورد نظر و یک راژه که به طور تصادفی از فرهنگ لغات به دست می آید(یا چیزهایی که در اطرافمان می بینیم) برقرار می کنیم. انتظار می رود هنگام تلاش برای برقراری چنین ارتباطی، ایده ها و نظرات جدیدی راجع به موضوع به دست  آوریم.اما اگر موفق نشویم، می توانیم واژه تصادفی دیگری را امتحان کنیم. به عنوان مثال، فرض کنید صاحب کارخانه تولید تلویزیون هستید و قصد دارید با استفاده از تکنیک واژه تصادفی، به ایده جدیدی در مورد تلویزیون دست یابید. به این منظور، فرهنگ لغات را باز کرده اید و به طور تصادفی به کلمه "پنیر" رسیده اید.با کمی دقت در حالت، صفات، مزایا، معایب ، وضع ظاهری و ترکیبات پنیر، می توان گفت چون پنیر دارای سوراخهایی است، پس تلویزیون هم باید دارای سوراخهایی باشد. به این ترتیب، طرح تلویزیونهایی که صفحه آنها بتواند همزمان تصاویر چند کانال را نمایش دهد در ذهن تداعی می شود. تمرین: سعی کنید با استفاده از تکنیک واژه تصادفی،ایده های جدیدی در مورد کفش مردانه، بستنی و میز تحریر به دست آورید. تکنیک "چه می شود اگر...؟" به طور کلی برای خلاق شدن می باید فکر انسان از قالبهای ذهنی،شرایط موجود، عادتها و پیش فرضهای موجود و ... آزاد شود تا بتواند به موضوع از ابعاد و زوایای مختلف بنگرد و ایده های جدیدی به ذهن خطور کند. بر همین اساس تکنیک "چه می شود اگر...؟" طراحی شده است تا کمک شایانی  به آزاد سازی فکر کند. در این روش توصیه می شود برای یافتن ایده های جدید یا راه حل خلاق مسئله، از گروه سوالات تکنیک "چه می شود اگر...؟" استفاده کنید و آن را به قدری تکرار و تمرین کنید تا برایتان یک عادت شود. به عنوان مثال، اگر قصد دارید در مورد ساختن یک مدادپاکن جدید ایده هایی به دست آورید می توانید سوال کنید:" چه می شود اگر  مداد پاک کنها خوراکی باشند؟" یا "چه می شود اگر مداد پاک کنها به صورت کیلویی فروخته شود؟" یا " چه می شود اگر کنار مداد پاک کنها (هواکش یا فن)برای مکش آشغالهای آن تعبیه شود؟" یا " چه می شود اگر عمل پاک کردن به وسیله اسپری انجام گیرد؟" از این تکنیک می توان برای پرورش قدرت خلاقیت، بدون داشتن موضوع خاصی استفاده کرد، ضمن اینکه به عنوان یک تفریح یا شوخی و سرگرمی نیز در همه اوقات قابل استفاده است. به عنوان مثال، می توان پرسید: ·        چه می شود اگر قد همه مردم یکسان باشد؟ ·        چه می شود اگر خریدار کتاب بتواند بخش یا بخش هایی از کتاب را بخرد؟ ·        چه می شود اگر به جای ماشینها، جاده ها (خیابانها) متحرک باشند؟ ·        چه می شود اگر همه قادر باشند افکار دیگران بخوانند؟ ·        چه می شود اگر ...

گام تصادفی (Random walk)

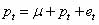
تست‌های اولیه در مورد کارایی بازار، عموماً مبتنی بر آزمون «گام تصادفی» بودن حرکت قیمت‌های سهام بود. ردشدن مدل گام تصادفی دلیلی بر عدم‌کارایی بازار تلقی می‌شد؛ بنابراین وجود هرگونه الگویی برای پیش‌بینی بازده سهام نشانگر نقض فرضیه بازار کارا بود. مدل‌های گام تصادفی پس از ارائه نظریه بازار کارا توسط فاما توسعه یافتند. فرض صفر چنین آزمون‌هایی وجود یکی از انواع گام تصادفی در حرکت قیمت‌هاست. کمپل، لو و مک‌کنلی (١٩٩٧) (Campbell, Lo, Mackinlay) انواع مدل‌های گام تصادفی ارائه‌شده را به‌همراه ویژگی‌های هریک جمع‌آوری کردند. یک مدل پایه گام تصادفی به صورت زیر است: که در آن Pt قیمت دارایی در زمان       بازده مورد انتظار، و فرضیات در مورد et در انواع مدل‌های گام تصادفی متفاوت می‌باشد. در میان مدل‌های گام تصادفی مدل RW1 محدودترین مدل است (یعنی بیشترین قیدها را به مدل تحمیل می‌کند)، و مدل‌های RW2 و RW3 به ترتیب محدودیت‌های کمتری روی مدل اعمال می‌کنند. در ادامه انواع مدل‌های گام تصادفی به‌طور اجمالی معرفی خواهد شد. مدل گام تصادفی نوع ١ مدل گام تصادفی نوع ١ ساده‌ترین نوع گام تصادفی است که پسماندها را مستقل و دارای توزیع یکسان (i.i.d) در نظر می‌گیرد. دینامیک بازده در این مدل به‌صورت زیر می‌باشد: در این مدل پسماندها مستقل از هم و با توزیع یکسان فرض شده‌اند، لذا مدل واریانس ناهمسانی (تغییرات تلاطم در طول زمان) و ویژگی خوشه‌ای بودن تلاطم (وجود همبستگی در تلاطم) بازده را نمی‌تواند توضیح دهد. استقلال پسماندها     بدین معناست که نه تنها پسماندها همبستگی ندارند، بلکه هر تابع غیرخطی از پسماندها نیز ناهمبسته هستند. چنان‌چه تلاطم بازده‌ها در طول زمان تغییرات قابل‌توجهی داشته باشد، فرضیه گام تصادفی با انجام آزمون مربوطه رد خواهد شد؛ اما، این مطلب (رد فرضیه گام تصادفی ١) ممکن است اطلاعاتی در خصوص پیش‌بینی‌پذیری بازده به ما ندهد. وجود هرگونه خودهمبستگی معنادار آماری در بازده‌ها و توان دوم بازده‌ها این فرضیه را رد خواهد کرد. با توجه به ویژگی‌های معمول سری‌های زمانی بازده، فروض این مدل بسیار قوی بوده و با دنیای واقعی، به‌ویژه در دوره‌های بلندمدت چندان سازگار نیست. مدل گام تصادفی ٢ یک مدل ساده گام تصادفی نوع ٢ به‌صورت زیر است: بنابراین مقدار انتظاری شرطی بازده در تمامی دوره‌ها یکسان خواهد بود، ضمن این‌که بازده‌ها از یکدیگر مستقل فرض شده‌اند، لذا هیچ‌یک از گشتاورهای بازده همبستگی ندارند. این مدل فرض یکسان بودن توزیع پسماندها را حذف می‌کند؛ بنابراین، امکان توضیح واریانس ناهمسانی را ...

پژو 206 مدل 81 دور رنگ بیمه برج 12 موتور( روغن سوزی دارد) قیمت 9 م