تبدیل فوریه

تبدیل فوریه

یک قضیه ریاضی می گوید که تقریبا همه توابع را می توان به عنوان مجموعه ای از دامنه های سینوسی و فرکانس های مختلف نشان داد. تبدیلات فوریه یک تکنیکی در ریاضیات است، که برای پیدا کردن دامنه ها و فرکانس های سینوسی آن می باشد. گسسته سازی تبدیلات فوریه –Discrete Fourier Transform - (DFT) یک الگوریتم که محاسبات برای داده های عددی می باشد. تبدیل فوریه سریع یک اجرا و پیاده سازی موثر و کارآمدی است. توبع زیر در متلب تبدیلات فوریه و عملیات مرتبط را انجام می دهد:تبدیل فوریه سریع یک بعدی fft تبدیل فوریه سریع دو بعدی fft2 تبدیل فوریه سریع چند بعدی fftn انتقال کندی (عقب افتادگی) صفر به مرکز تبدیل fftshift معکوس تبدیل فوریه سریع یک بعدی ifft معکوس تبدیل فوریه سریع دو بعدی ifft2 معکوس تبدیل فوریه سریع چند بعدی ifftn قدر مطلق (اندازه اعداد مختلط) abs زاویه angle مرتب کردن اعداد مختلط بر اساس جفت های مزدوج مختلط cplxpair توان دو به بعد nextpow2 زاویه فاز صحیح unwarp دستور fft برای یک بردار ستونی:>> y = [2 0 1 0 2 1 1 0]';>> Y= fft (y) Y = 7.0000 -0.7071 + 0.7071i 2.0000 - 1.0000i 0.7071 + 0.7071i 5.0000 0.7071 - 0.7071i 2.0000 + 1.0000i -0.7071 - 0.7071i اولین مقدار Y مجموع عناصر y است، و دامنه هایی که ازفرکانس های صفر یا ثابت هستند جزئی از سری فوریه هستند. عبارات 2 تا 4 (اعداد مختلط) دامنه هایی از فرکانس های مثبت مولفه های فوریه هستند. عبارت 5 دامنه ای از عنصر در فرکانس نایکوئیست، که نیمی از فرکانس نمونه برداری شده است. سه عبارت آخرمولفه های فرکانس های منفی هستند، که برای سیگنال های واقعی(real) ترکیبات اعداد مختلط از مولفه های فرکانس های مثبت هستند.تابع fftshift برای تنظیم یک تبدیل فوریه که در آن منفی و مثبت در دو طرف فرکانس صفر قرار می گیرد.fftshift(Y) ans = 5.0000 0.7071 - 0.7071i 2.0000 + 1.0000i -0.7071 - 0.7071i 7.0000 -0.7071 + 0.7071i 2.0000 - 1.0000i 0.7071 + 0.7071i و قدر مطلق Y برابر است با:>> abs(Y) ans = 7.0000 1.0000 2.2361 1.0000 5.0000 1.0000 2.2361 1.0000 معکوس سری فوریه Y را با تابع ifft بدست می آوریم:>> ifft(Y) ans = 2.0000 -0.0000 1.0000 0 2.0000 1.0000 1.0000 0 >> y y = 2 0 1 0 2 1 1 0 -----------------------------------

تبدیلات فوریه (1)

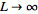
تبدیلات فوریه به طور کلی، تعمیم سری فوریه مختلط در حالتی است که حد برقرار باشد. این کار را می توان با تعویض سری مجزای با حاصل ضرب یک انتگرالده در دیفرانسیل متغیر آن و نیز فرض انجام داد. سپس سری را به شکل یک انتگرال می نویسیم و معادلات برابر خواهند بود با در اینجا که تبدیل فوریه ی پیشرو () نامیده می شود و تبدیل فوریه وارونه () یا وارون تبدیل فوریه نامیده می شود. نماد در ترات (M.Trott) معرفی شده است (2004, p. xxxiv)، و و بعضی اوقات به ترتیب تبدیل فوریه و تبدیل فوریه ی وارونه نامیده می شوند که غالباْ با همین نام ها شناخته و مرسوم هستند (Krantz 1999, p. 202). برخی از نویسندگان (خصوصاً فیزیکدانان) ترجیحاْ در نوشتار این تبدیل از بسامد زاویه ای به جای بسامد نوسان استفاده می کنند. اگرچه این به تقارن لطمه می که زوج تبدیلاتی زیر را نتیجه می دهد برای برگرداندن تقارن تبدیلات، قرارداد را بکار می گیریم که در برخی منابع از آن ها استفاده شده است (Mathews and Walker 1970, p. 102). معمولاْ، زوج تبدیل فوریه ممکن است دو ثابت دلخواه و بکار برده شوند. مانند هر تابعی را می توان همانند رابطه ی زیر به دو جزء زوچ و فرد تقسیم کرد تبدیل فوریه را می توان همواره به صورت جملاتی از تبدیل cos فوریه (Fourier cosine transform) و تبدیل sin فوریه (Fourier sine transform) نوشت که تابع یک تبدیل به جلو و یک تبدیل فوریه ی وارون را در برمی گیرد (for continuous x را بخوانید پیوسته است در x) ۱- انتگرال وجود داشته باشد. ۲- تعداد ناپیوستگی ها، متناهی باشد. ۳- تابع در شرایط مرزی صدق می کند. لذا حداقل باید موید شرط کافی و ضعیف لیپ شیتس باشد. بنابر این شرط هر تابع با ازای هر در صادق باشد اگر برای تمام ، که و مستقل باشند و و . همچنین به ازای تمامیها یک کران بالا محسوب می شود. در این صورت وجود خواهد داشت ای که متناهی باشد (Ramirez 1985, p. 29). همچنین هموار کننده ی یک تابع (تعداد مشتق های پیوسته ی بزرگتر) توسط تبدیل فوریه، فشرده می شود. تبدیل فوریه یک تبدیل خطی است، برای اینکه اگر و به ترتیب تبدیل فوریه و باشند، آنگاه بنابراین تبدیل فوریه، همچنین متقارن است. زیرا و . نماد به عنوان کانولوشن (convolution)، ...
تبدیل فوریه

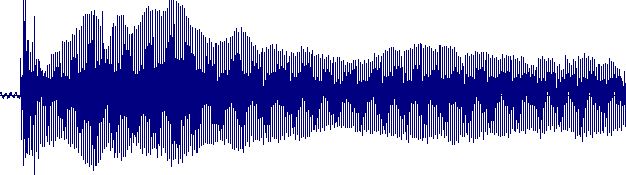
همانطور که می دانید مهمترین ویژگی در ادای هر حرف فرکانس های تشکیل دهنده آن حرف می باشد. به عنوان مثال سه فرکانس اصلی حرف " آ " فرکانس های 750 ، 1150 و 2400 هرتر بوده و همین فرکانس های برای حرف " او " 400 ، 1150 و 2300 هرتز می باشند. بنابراین آنچه باعث تفکیک دو حرف " آ " و " او " از همدیگر می شود، فرکانس های تشکیل دهنده آن می باشد. از اینرو در کاربردهای پردازش گفتار پیدا کردن فرکانس های تشکیل دهنده یک سیگنال گفتاری از اهمیت بسیار زیادی برخوردار می باشد. همانطور که می دانید سیگنال گفتار به شکل یک سیگنال زمانی در اختیار ما قرار دارد و تشخیص فرکانس های تشکیل دهنده یک سیگنال در حوزه زمانی غیرممکن است. به عنوان مثال شکل زیر را که نشان دهنده سیگنال گفتار زمانی حرف " آ " می باشد در نظر بگیرید. بخشی از این سیگنال به شکل زوم شده در شکل نشان داده شده است. از این شکل پیداست که پیدا کردن فرکانس های تشکیل دهنده این سیگنال از روی سیگنال زمانی غیررممکن می باشد. از اینرو نیاز به ابزار دیگری داریم که بتواند این کار را برای ما انجام دهد. آقای فوریه نشان دادند که هر تابع متناوب را می توان به شکل ترکیبی از موج های سینوسی ( یا کوسینوسی ) نشان داد که این مطلب را با نام سری های فوریه می شناسیم. از مقاله مربوطه به موج سینوسی به یاد دارید که هر موج سینوسی می تواند به شکل یک صوت در خروجی بلندگو به شنیده شود. در این بین فرکانس موج سینوسی نیز مستقیما زیر و بم بودن صوت تولید شده را تعیین می کند. با توجه به این دو حقیقت می توان دریافت که با استفاده از آنالیز فوریه یک سیگنال می توان موج های سینوسی تشکیل دهنده آن را استخراج کرد و از روی موج های سینوسی نیز می توان فرکانس های تشکیل دهنده سیگنال گفتار را به دست آورد. با این حال نمی توان مستقیما از سری های فوریه برای این منظور بهره جست. چراکه سری های فوریه بر روی توابع متناوب تعریف شده اند و این در حالی است که ما در اینجا با سیگنال سروکار داریم که هیچ تابعی را نمی توان برای یک سیگنال گفتار تخمین زد. برای رفع این مشکل ابزاری با نام تبدیل فوریه معرفی شده است که بر روی داده های عددی ( سیگنال ) اعمال می شود. تبدیل فوریه گسسته مختلط سیگنال s به طول N را می توان با استفاده از رابطه زیر تعریف کرد: از قانون اویلر نیز به یاد دارید که : بنابراین رابطه فوق را می توان به شکل زیر بازنویسی کرد : که در این رابطه N اندازه سیگنال ورودی ، s(n) مقدار سیگنال ورودی در نقطه n ، m اندیس فرکانس، S(m) اندازه فرکانس در اندیس m ام می باشند. همانطور که می دانید S(m) یک عدد مختلط است و بنابراین برای به دست اندازه فرکانس در اندیس mام باید ...
تبدیل فوریه
سری فوریه، روشی در ریاضیات می‌باشد که به وسیله آن، هر تابع متناوبی به صورت جمعی از توابع سینوس و کسینوس می‌تواند نوشته شود. نام این قضیه به اسم ریاضیدان فرانسوی، ژوزف فوریه ثبت شده است. اگر یک تابع متناوب با دوره تناوب T باشد (یا به عبارتی: ‎f(t + T) = f(t)‎) و بطور مطلق انتگرال‌پذیر باشد، آنگاه این تابع را می‌توان به صورت زیر نوشت: که در آن ωn هارمونیک nام سری فوریه به رادیان بوده و ضرایب an، a0 و bn را می‌توان از فرمول‌های اولر بدست آورد.
تبدیل فوریه

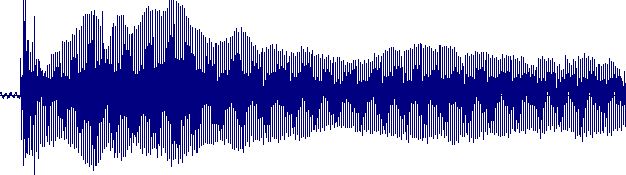
همانطور که می دانید مهمترین ویژگی در ادای هر حرف فرکانس های تشکیل دهنده آن حرف می باشد. به عنوان مثال سه فرکانس اصلی حرف " آ " فرکانس های 750 ، 1150 و 2400 هرتر بوده و همین فرکانس های برای حرف " او " 400 ، 1150 و 2300 هرتز می باشند. بنابراین آنچه باعث تفکیک دو حرف " آ " و " او " از همدیگر می شود، فرکانس های تشکیل دهنده آن می باشد. از اینرو در کاربردهای پردازش گفتار پیدا کردن فرکانس های تشکیل دهنده یک سیگنال گفتاری از اهمیت بسیار زیادی برخوردار می باشد. همانطور که می دانید سیگنال گفتار به شکل یک سیگنال زمانی در اختیار ما قرار دارد و تشخیص فرکانس های تشکیل دهنده یک سیگنال در حوزه زمانی غیرممکن است. به عنوان مثال شکل زیر را که نشان دهنده سیگنال گفتار زمانی حرف " آ " می باشد در نظر بگیرید. بخشی از این سیگنال به شکل زوم شده در شکل نشان داده شده است. از این شکل پیداست که پیدا کردن فرکانس های تشکیل دهنده این سیگنال از روی سیگنال زمانی غیررممکن می باشد. از اینرو نیاز به ابزار دیگری داریم که بتواند این کار را برای ما انجام دهد. آقای فوریه نشان دادند که هر تابع متناوب را می توان به شکل ترکیبی از موج های سینوسی ( یا کوسینوسی ) نشان داد که این مطلب را با نام سری های فوریه می شناسیم. از مقاله مربوطه به موج سینوسی به یاد دارید که هر موج سینوسی می تواند به شکل یک صوت در خروجی بلندگو به شنیده شود. در این بین فرکانس موج سینوسی نیز مستقیما زیر و بم بودن صوت تولید شده را تعیین می کند. با توجه به این دو حقیقت می توان دریافت که با استفاده از آنالیز فوریه یک سیگنال می توان موج های سینوسی تشکیل دهنده آن را استخراج کرد و از روی موج های سینوسی نیز می توان فرکانس های تشکیل دهنده سیگنال گفتار را به دست آورد. با این حال نمی توان مستقیما از سری های فوریه برای این منظور بهره جست. چراکه سری های فوریه بر روی توابع متناوب تعریف شده اند و این در حالی است که ما در اینجا با سیگنال سروکار داریم که هیچ تابعی را نمی توان برای یک سیگنال گفتار تخمین زد. برای رفع این مشکل ابزاری با نام تبدیل فوریه معرفی شده است که بر روی داده های عددی ( سیگنال ) اعمال می شود. تبدیل فوریه گسسته مختلط سیگنال s به طول N را می توان با استفاده از رابطه زیر تعریف کرد: از قانون اویلر نیز به یاد دارید که : بنابراین رابطه فوق را می توان به شکل زیر بازنویسی کرد : که در این رابطه N اندازه سیگنال ورودی ، s(n) مقدار سیگنال ورودی در نقطه n ، m اندیس فرکانس، S(m) اندازه فرکانس در اندیس m ام می باشند. همانطور که می دانید S(m) یک عدد مختلط است و بنابراین برای به دست اندازه فرکانس در اندیس mام باید بزرگی این عدد مختلط ...
تبدیل فوریه

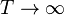
تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک انتقال انتگرالی است که هر تابع f(t) را به یک تابع دیگر F(ω) منعکس می‌کند. به F(ω) در این صورت تبدیل‌شده فوریه۱ تابع f(t) می‌گویند. حالت خاص انتقال فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع f(t) متناوب باشد، یعنی: f(t + T) = f(t) . حال اگر تابع متناوب نباشد و یا به عبارتی، تناوب آن برابر بی‌نهایت باشد <?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" />)<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />)، آنگاه از سری فوریه به راحتی، عبارت زیر به دست می‌آید: انتقال فوریه و همراه آن آنالیز فوریه، در مباحث مختلف فیزیک، از جمله الکترونیک و الکترومغناطیس (به خصوص در پیغام‌رسانی و مخابرات)، آکوستیک، فیزیک امواج و غیره کاربرد فراوان دارد.
تبدیلات فوریه (2)

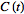
۱) قضیه ی وینر - خین اگر تعریف تابع خودهمبستگی (autocorrelation) تابعی نظیر را به خاطر بیاوریم، همچنین می دانیم که تبدیل فوریه ی به صورت زیر است که همیوغ مختلط آن نیز به صورت زیر نوشته می شود: با وارد کردن و به تابع خودهمبستگی آنگاه داریم که تابع دلتای دیراک (Delta Function) است. تعجب آور است که خودهمبستگی به سادگی توسط تبدیل فوریه ی مربع قدرمطلق به دست آمد. قضیه ی وینر - خین چن حالت خاصی از قضیه ی کلی تر همبستگی متقابل (cross-correlation theorem) زمانی که . ۲) همبستگی متقابل را همبستگی متقابل توابع و می نامیم که عددی حقیقی است که به صورت زیر تعریف می شود که نماد کانولوشن و همیوغ مختلط (complex conjugate) می باشد. چون کانولوشن از طریق معادله ی زیر قابل محاسبه است در نتیجه با فرض و معادله ی اخیر به شکل زیر تبدیل می شود همبستگی متقابل در رابطه ی زیر نیز صدق می کند اگر و تابعی زوج (even) باشند آنگاه که همان کانولوشن است. ۳) قضیه ی همبستگی متقابل با فرضیات فوق می توانیم به شکل زیر بسط دهیم که تبدیل فوریه و همیوغ مختلط هستند. و نیز با بکار بردن یک تبدیل فوریه در هر طرف، قضیه ی همبستگی متقابل بدست خواهد آمد منابع: Bracewell, R. "Pentagram Notation for Cross Correlation." The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 46 and 243, 1999. Papoulis, A. The Fourier Integral and Its Applications. New York: McGraw-Hill, pp. 244-245 and 252-253, 1962.
تبدیل فوریه

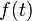
تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک تبدیل انتگرالی است که هر تابع را به یک تابع دیگر منعکس می‌کند. در این صورت، به تبدیل‌ فوریهٔ تابع می‌گویند. حالت خاص تبدیل فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع متناوب باشد، یعنی: . چنانچه تابع متناوب نباشد و یا به عبارتی، تناوب آن برابر بی‌نهایت باشد ()، از سری فوریه به راحتی، عبارت زیر به دست می‌آید: تبدیل فوریه و به همراه آن آنالیز فوریه، در مباحث مختلف فیزیک، از جمله الکترونیک و الکترومغناطیس (به خصوص در پیغام‌رسانی و مخابرات)، آکوستیک، فیزیک امواج و غیره کاربرد فراوان دارد.تبدیلات فوریه در محاسبات تصویری کاربرد های وسیعی دارند. بطور مثال در ام‌آرآی در فیزیک پزشکی اطلاعات امواج ساطع شده از هسته های هیدرژن از فرم دامنه فرکانسی (frequency domain) به فرم دامنه فضایی (spatial domain) جهت ایجاد تصویر نهایی تبدیل فوریه می‌شوند.
تبدیل فوریه
همانطور که می دانید سیگنال گفتار به شکل یک سیگنال زمانی در اختیار ما قرار دارد و تشخیص فرکانس های تشکیل دهنده یک سیگنال در حوزه زمانی غیرممکن است. به عنوان مثال شکل زیر را که نشان دهنده سیگنال گفتار زمانی حرف " آ " می باشد در نظر بگیرید. بخشی از این سیگنال به شکل زوم شده در شکل نشان داده شده است.از این شکل پیداست که پیدا کردن فرکانس های تشکیل دهنده این سیگنال از روی سیگنال زمانی غیررممکن می باشد. از اینرو نیاز به ابزار دیگری داریم که بتواند این کار را برای ما انجام دهد. آقای فوریه نشان دادند که هر تابع متناوب را می توان به شکل ترکیبی از موج های سینوسی ( یا کوسینوسی ) نشان داد که این مطلب را با نام سری های فوریه می شناسیم. از مقاله مربوطه به موج سینوسی به یاد دارید که هر موج سینوسی می تواند به شکل یک صوت در خروجی بلندگو به شنیده شود. در این بین فرکانس موج سینوسی نیز مستقیما زیر و بم بودن صوت تولید شده را تعیین می کند.با توجه به این دو حقیقت می توان دریافت که با استفاده از آنالیز فوریه یک سیگنال می توان موج های سینوسی تشکیل دهنده آن را استخراج کرد و از روی موج های سینوسی نیز می توان فرکانس های تشکیل دهنده سیگنال گفتار را به دست آورد. با این حال نمی توان مستقیما از سری های فوریه برای این منظور بهره جست. چراکه سری های فوریه بر روی توابع متناوب تعریف شده اند و این در حالی است که ما در اینجا با سیگنال سروکار داریم که هیچ تابعی را نمی توان برای یک سیگنال گفتار تخمین زد. برای رفع این مشکل ابزاری با نام تبدیل فوریه معرفی شده است که بر روی داده های عددی ( سیگنال ) اعمال می شود. تبدیل فوریه گسسته مختلط سیگنال s به طول N را می توان با استفاده از رابطه زیر تعریف کرد:از قانون اویلر نیز به یاد دارید که :بنابراین رابطه فوق را می توان به شکل زیر بازنویسی کرد : که در این رابطه N اندازه سیگنال ورودی ، s(n) مقدار سیگنال ورودی در نقطه n ، m اندیس فرکانس، S(m) اندازه فرکانس در اندیس m ام می باشند. همانطور که می دانید S(m) یک عدد مختلط است و بنابراین برای به دست اندازه فرکانس در اندیس mام باید بزرگی این عدد مختلط را محاسبه کرد. بزرگی یک عدد مختلط از رابطه زیر به دست می آید :پس از آنکه تبدیل فوریه بر روی سیگنال ورودی اعمال شد، بردار S در فرکانس های تشکیل دهنده سیگنال s دارای مقداری بسیار بزرگتر از 0 و در سایر نقاط بزرگی نزدیک به صفر خواهد داشت. بنابراین می توان برای پیدا کردن فرکانس های تشکیل دهنده یک سیگنال گفتار تبدیل فوریه را بر روی سیگنال ورودی اعالم کرده و پس از محاسبه بزرگی خروجی، فرکانس های تشکیل دهنده آن سیگنال را از روی بزرگی هر فرکانس استخراج ...
طیف سنجی مادون
طیف سنجی مادون قرمز ، روشی برای شناساییمولکولهاو بخصوص گروه عاملی مولکولهاست. هر ماده‌ای ، طیف مادون قرمز مخصوص به خود دارد و همانند اثر انگشت ، مختص خود مولکول می‌باشد. دستگاهی که طیف جذبی یک ترکیب را حاصل می‌کند، یک دستگاه طیف سنج مادون قرمز یا به عبارت دقیقتر یک اسکپتروفتومتر خوانده می‌شود.دو نوع دستگاه طیف سنج مادون قرمز در آزمایشگاههای شیمی آلیبطور معمول مورد استفاده قرار می‌گیرد؛ دستگاههای تفکیکی (پراکندگی) و تبدیل فوریه (FT). هر دو دستگاه ، طیفهای ترکیبات را در محدوده4000cm تا400cm فراهم می‌کنند. گرچه هر دو دستگاه ، طیفهای تقریبا یکسانی را برای یک ترکیب مشخص ارائه می‌دهند، ولی طیف سنج مادون قرمز FT ، طیف مادون قرمز را به مراتب سریعتر از دستگاههای تفکیکی تولید می‌کنند. نور مادون قرمز اسپکتروفوتومتر مادون قرمز در شناسایی مولکولی و ارتعاشات وابسته به ساختار آن استفاده می شود.‌‌ ‌ساختارهای شیمیایی متفاوت، به دلیل تفاوت در انرژی های مربوط به هر طول موج، راه‌های مختلفی در پاسخ به طول موج های مختلف دارند. به عنوان مثال مادون قرمز‌های برد متوسط، تمایل به لرزش دورانی دارد، درحالیکه مادون قرمز نزدیک (با انرژی بالاتر) تمایل به لرزش هارمونیک مولکولی مانند جنبش دارددر اسپکتروفوتومترهای‌IR متداول یک پرتو مادون قرمز مستقیما به نمونه می تابد و تمام طول موج‌های طیف نسبت به پرتو مرجع اندازه‌گیری می‌شود. به منظور تولید طیفی با کیفیت بالا، باید پهنای طیف ورودی به آرامی اسکن شوداسپکتروسکوپی‌IR با روش بسط تبدیل فوریه اصلاح می شود. قلب اسپکتروفوتومترهای IR تداخل سنج میشلسون است که در شکل نشان داده شده است نور تابش شده از منبع‌IR به سمت سلول‌های نمونه هدایت می شود. نیمی از پرتو تابشی از آینه ثابت باز تابیده شده و نیم دیگر آن از آینه ای که مرتبا در فاصله ای حدود دو و نیم میکرومتر حرکت می کند منعکس می‌شود. هنگامی که دوباره دو پرتو در آشکارساز با هم ترکیب می شوند و تداخل به وجود می آید، حدود دو ثانیه یک اسکن از فاصله ورودی گرفته شده و در کامپیوتر ذخیره می شود. به همین ترتیب چندین اسکن دیگر نیز به طور همزمان به آن اضافه می شود. با توجه به نوسانات و ارتعاشات حرارتی در آزمایشگاه بدیهی است که این امر نا ممکن است. پس به منظور حل این مشکل از لیزر هلیم – نئون برای تاباندن به تداخل سنج میشلسون استفاده می شود و تداخل لیزر به عنوان فرکانس مرجع به کار گرفته می شود. استفاده از اسپکتروفوتومتر اسپکتروفوتومترها مستقیما برای اندازه‌گیری شدت نور در طول موج های مختلف استفاده می شود و می‌تواند نماینده درصد نور تابشی ...
سری فوریه (تکمیلی)

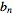
برای تابع متناوب در یک بازه مثل به جای ، یک تغییر ساده ی متغیرها می تواند برای تبدیل بازه ی انتگرالگیری از به مورد استفاده قرار بگیرد. فرض کنیم: با حل معادله اول نسبت به داریم ، لذا با وارد کردن این به خواهیم داشت: بنابراین: به طور یکسان، برای تابعی که در بازه ی تعریف می شود، معادلات بالا به سادگی به اشکال زیر تبدیل می شوند: در حقیقت برای تابع متناوب با دوره ی ، هر بازه ی با توجه به یکی از دو اصل راحتی یا اولویت شخصی می تواند بکار گرفته شود (Arfken 1985, p. 769). ضرایب (coefficients) برای بسط های سری های فوریه ی تعدادی از توابع مرسوم در Beyer, 1987, pp. 411-412 و Byerly, 1959, p. 51 آمده است. یکی از مرسوم ترین توابعی که با استفاده از تکنیک اخیر مورد تجزیه تحلیل قرار می گیرد، موج چهار گوش یا مربعی (square wave) است. سری های فوریه برای تعدادی از توابع مرسوم در جدول زیر گرداوری شده اند. تابع سری فوریه سری های فوریه---موج دندانه اره ای سری های فوریه---موج مربعی سری های فوریه---موج مثلثی اگر یک تابع زوج باشد، یعنی ، آنگاه زوج است. (این بدان خاطر است که چون فرد است و یک تابع زوج (even function) ضرب در یک تابع زوج برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها . به طور یکسان، اگر یک تابع فرد است، پس ، آنگاه فرد است. (این بدان خاطر است که چون زوج است و یک تابع زوج (even function) ضرب در یک تابع فرد برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها نظریه ی سری های فوریه همچنین می تواند به ضرایب مختلط (complex coefficients) بسط داده شود. یک تابع حقیقی-مقدار را در نظر می گیریم. می نویسیم: حال بررسی می کنیم که لذا ضرایب (coefficients) را می توان برحسب آنهایی که در سری های فوریه گفته شده اند، توضیح داد: برای یک تابع متناوب در ، اینها به شکل های زیر تبدیل خواهند شد: این معادلات مبنای مهمی برای شکل گیری تبدیل فوریه (Fourier transform) محسوب می شوند که با تبدیل از یک متغیر مجزا به یک متغیر پیوسته در طول بدست می آید. لینک مربوطه: سری فوریه منابع: Arfken, G. "Fourier Series." Ch. 14 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 760-793, 1985. Askey, R. and Haimo, D. T. "Similarities between Fourier and Power Series." Amer. Math. Monthly 103, 297-304, 1996. Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, ...