انتگرال دوگانه
انتگرال دوگانه
انتگرال دوگانه همانطور که تعریف مساحت زیر منحنی انگیزه تعریف انتگرال توابع با یک متغیر است، مفهوم حجم زیر یک سطح نیز ما را به تعریف انتگرال توابع با دو متغیر ، به نام انتگرال دو گانه ، رهنمون می کند. انتگرال دو گانه بسیار شبیه انتگرال میباشد، با این تفاوت که در این نوع انتگرال قلمرو در صفحه دو بعدی واقع شده است. انتگرال دو گانه روی نواحی مستطیلی فرض می کنیم بر ناحیه ی مستطیلی زیر تعریف شود: و فرض می کنیم با شبکه ای از خطوط موازی با محور های و پوشیده شده باشد. مساحت هر کدام از این قطعه های کوچک برابر است با : این قطعات را شماره گذاری می کنیم و در هر قطعه ای مانند نقطه ی را بر می گزینیم و مجموع زیر را تشکیل می دهیم: اگر در سراسر پیوسته یاشد، با کوچک کردن خانه های شبکه یعنی میل دادن و به صفر،مجموع مشخص شده در رابطه ی فوق به حدی میل می کند که آن را انتگرال دوگانه ی روی می نامیم. نماد انتگرال دوگانه عبارت است از : یا بنابر این: قضیه فوبینی (صورت اول): اگر بر ناحیه مستطیلی پیوسته باشد، داریم: قضیه فوبینی (صورت قوی تر): فرض می کنیم روی ناحیه ای چون پیوسته باشد. ۱- اگرتعریف عبارت باشد از : ، با این شرط که و بر پیوسته باشد، آنگاه : ۲- اگرتعریف عبارت باشد از : ، با این شرط که و بر پیوسته باشد، آنگاه : دامنه در انتگرال دو گانه دو دامنه در انتگرال دو گانه وجود دارد: دامنه منظم: دامنهای است که هر خط موازی محورهای مختصات محیط آن را حداکثر در دو نقطه قطع کند. مانند مربع ، مثلث ، دایره. در این نوع دامنه تعویض حدود انتگرال نسبتا ساده است. دامنه غیرمنظم: دامنهای که هر خط موازی محورهای مختصات آن را در بیش از دو نقطه قطع کند مانند سطح بین دو دایره یا دو مربع. در این نوع دامنه ها تعویض حدود باید با احتیاط صورت گیرد. برخی از انواع دامنههای منظم در انتگرال دو گانه : این دامنه به شکل مربع یا مستطیلی است که اضلاع آن موازی محورهای مختصات است. دامنههای مثلثی مانند: و در صورت تعویض انتگرال گیری میتوان آن را به صورت نوشت. دامنههای دایرهای؛ دامنههای دایرهای در دستگاه دکارتی و قطبی به صورت زیر نوشته میشوند: دایرهای که مرکز آن در مبدا مختصات و شعاع آن باشد. دکارتی: قطبی: تعویض انتگرال ها ی دوگانه مانند مشتقات جزئی، انتگرال نیز دارای ترتیب است. وقتی انتگرال به صورت باشد، یعنی باید ابتدا را ثابت فرض کرده و نسبت به متغیر انتگرال گرفت و در مرحله دوم نسبت به انتگرال بگیریم. چنانچه حدود به صورت و باشد میتوانیم در صورت لزوم را بر حسب تابعی از نوشته و حدود را از روی شکل دامنه بدست آورده و در انتگرال قرار ...
انتگرال دوگانه
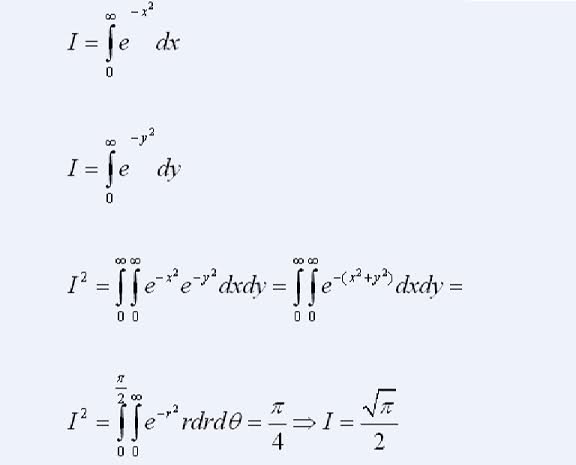
به انتگرال زیر توجه کنید این انتگرال معین به راحتی قابل محاسبه نیست مگر این که از انتگرال دوگانه کمک بگیریم .مراحل کار به صورت زیر هست: اسم انتگرال را I می ذاریم .چون انتگرال معین هست و یک عدد جوابش می باشد تغییر متغییر از x به y تاثیری در جواب ان ندارد پس حاصل ان نیز هم I می شود این دو را در هم ضرب و بعد از خواص تابع e کمک گرفته و با توجه به تکنیکهای انتگرال دوگانه و روش تغییر متغییر به مختصات قطبی به راحتی جواب مسئله پیدا می شود . اکنون مراحل بالا را پیاده می کنیم یعنی:
جزوه مسائل حل شده انتگرال دوگانه
انتگرال دوگانه یکی از مباحث مطرح شده در برخی از واحد های دانشگاهی است به عنوان مثال دانشجویان مهندسی در درس ریاضی عمومی 2 با این مبحث آشنامیشوند و همچنین برای کنکور کارشناسی ارشد هم باید این مبحث را مطالعه کرد به همین دلیل برای شما جزوه ای را تهیه کرده ام که حاصل زحمات استاد گرامی باقر کرامتی است و شامل حل مسائلی در انتگرال دوگانه میباشدکه موارد مطرح شده در این جزوه به شرح زیر است
جزوات انتگرال دوگانه و معادلات ديفرانسيل دكتر نيكوكار
با سلام و تبریک شروع به کار وبلاگ یک جزوه ی تكميل برای بحث انتگرال دوگانه درس ریاضی ۲ که حتما" بدردتون میخوره كه مجموعه مباحث اون از این قراره 1- رسم ناحیه انتگرال گیری 2- محاسبه انتگرال دوگانه در مختصات دکارتی 3- محاسبه انتگرال دوگانه در مختصات قطبی 4- محاسبه انتگرال دوگانه با استفاده از تغییر و متغییر 5- محاسبه انتگرال دوگانه غیر عادی 6- محاسبه حجم با استفاده از انتگرال دوگانه 7- محاسبه سطح رویه و انتگرال رویه ای از اینجا دانلود کنین و یک مجموعه جزوه ی تدریس شده توسط دکتر نیکوکار برای معادلات دیفرانسلی که تقریبا" کاملترین تدریس ممکن برای معادلات دیفرانسل كه این جزوه بدلیل حجم نسبتا" بالا در چند قسمت ارائه شده قسمت اول قسمت دوم قسمت سوم قسمت چهارم قسمت پنجم
جزوه مسائل حل شده انتگرال دوگانه
جزوه مسائل حل شده انتگرال دوگانه انتگرال دوگانه یکی از مباحث مطرح شده در برخی از واحد های دانشگاهی است به عنوان مثال دانشجویان مهندسی در درس ریاضی عمومی 2 با این مبحث آشنامیشوند و همچنین برای کنکور کارشناسی ارشد هم باید این مبحث را مطالعه کرد به همین دلیل برای شما جزوه ای را تهیه کرده ام که حاصل زحمات استاد گرامی ليتهلد وتوماس است و شامل حل مسائلی در انتگرال دوگانه میباشدکه موارد مطرح شده در این جزوه به شرح زیر است 1- رسم ناحیه انتگرال گیری 2- محاسبه انتگرال دوگانه در مختصات دکارتی 3- محاسبه انتگرال دوگانه در مختصات قطبی 4- محاسبه انتگرال دوگانه با استفاده از تغییر و متغییر 5- محاسبه انتگرال دوگانه غیر عادی 6- محاسبه حجم با استفاده از انتگرال دوگانه 7- محاسبه سطح رویه و انتگرال رویه ای این کتاب 60 صفحه ای 4 مگابایت حجم دارد دانلود
