اثبات رابطه ی برنولی
اندازه گیری سرعت و دبی
-1- اندازه گیری سرعت و دبی (Velocity & Flow Measurment) کنترل سرعت به عنوان یکی از سنجش های پایه ای در سیالات است. به وسیله ی اندازه گیری سرعت عبوری از یک مقطع مشخص می توان به اندازه ی دبی سیال در آن نقطه دست یافت و همچنین با استفاده از رابطه ی برنولی و دانستن چگالی سیال می توان به سرعت در سایر نقاط در مسیر جریان دست یافت. وسایل گوناگون و ارزان موجود برای اندازه گیری مقدار سرعت را می توان برای بدست آوردن اطلاعات در جریان های دارای موج های غیر در هم و تغییرات آهسته به کار برد. برای نمونه گیری از نوسانات موجی و در هم که سرعت زیاد دارند لازم است دقت نمونه برداری بیشتر باشد. در بسیاری از کاربردهای اندازه گیری سرعت که به منظور کالیبراسیون دستگاه های دبی سنج انجام می شود، فقط اولین سطح اندازه گیری سرعت ضرورت دارد. [6] از آنجایی که شباهت میان دستگاه های دبی سنجی سرعت سنجی زیاد است ، گونه های این دو وسیله ی اندازه گیری را در این بخش با هم می آوریم: 3-1-1- لوله ی پیتوت (Pitot tube) لوله پیتوت یکی از دقیق ترین روش های اندازه گیری سرعت می باشد. [6] از لوله های پیتوت ، برای اندازه گیری سرعت و فشارهای موضعی سیال استفاده می شود. همچنین از آن ها برای اندازه گیری دبی سیالات برای آزمایش ها ، مطالعات تحقیقاتی ، و کاربردهای مشابه استفاده می شود. نوع خاصی از لوله های پیتوت برای اندازه گیری سرعت در هواپیما استفاده می شود. اساسا یک لوله پیتوت با تعیین اختلاف بین فشار کل (هد کل) و یا فشار ضربه ای (Impact Pressure) و فشار استاتیک ، اندازه گیری سرعت و دبی را انجام می دهد. اختلاف فشار های مذکور که فشار سینتیک نامیده می شود ، به وسیله ی رابطه ای که از قانون برنولی بدست می آید با سرعت ارتباط پیدا می کند. پس برای پیدا کردن فشار دینامیکی (جنبشی) و در نتیجه بدست آوردن سرعت در نقطه ی معینی از خطوط جریان سیال ، ضروری است تا اختلاف بین فشار استاتیک و فشار کل (فشار ضربه ای) مشخص شود. فشار کل به وسیله ی لوله ی فشار کل یا لوله ی فشار (Pressure Tube) اندازه گرفته می شود. لوله ی فشار به صورتی نصب می شود که سطح دهانه ی آن روبروی خطوط جریان سیال قرار گیرد و فشار استاتیک به وسیله ی یک یا چند مجرا که در جداره ی لوله عبور سیال تعبیه شده اندازه گیری می شود. از آن جایی که سرعت سیال در یک نقطه ی معین با استفاده از اختلاف فشار (Pt - Ps) بدست می آید ، در سر لوله های حس کننده فشار کل و استاتیک باید به یک ستون مایع فشار پایین (Liquid-Column Low Pressure) و یا به یک مانومتر اختلاف فشارسنج متصل گردند. برای این کار میزان بالا رفتن سطح مایع ، تحت تاثیر نیروی وارده از سیال تعیین می شود. در رابطه ی برنولی یک پارامتر مربوط ...
آیرودینامیک
حرکت آونگ بتدریج کند میشود و کوشید رابطه ی بین سرعت ومقاومت هوا راتعین کند. آزمایش گالیله عبارت بود از دو آونگ همانند که از دو کره ی با وزن یکسان آویزان از نخهای با طول برابر تشکیل میشدند.یکی را به اندازه ی 10 درجه و دیگری را به اندازه ی 160 درجه از وضع قائم منحرف و سپس رها کرد.بعد از مدت معینی تعداد نوسانهایی که آونگها انجام داده بودند با هم برابر بود.گالیله با توجه به نسبت سرعتها 1 و 16 فکر کرد مقاومت هوا با سرعت متناسب است .اما تنها نیوتن بود که قانون تناسب مقاومت هوا با مجذور سرعت مجذور ابعاد خطی جسم و چگالی هوا را بیان کرد.به علاوه این دانشمند انگلیسی اساس کار اتاق دمش را ریخت که سه قرن بعد تحقق یافت.بعدها برای سرعتهای بالاتر نادرستی متناسب بودن مقاومت هوا با مجذور سرعت به اثبات رسید.در واقع آزمایشهای حرکتهای پرتابی نشان داد که مقاومت هوا در مقابل پیشروی پرتابه ها خیلی بیش از مجذور سرعت افزایش می یابد .از همان هنگام کوششهای مربوط به پیشبرد هیدرودینامیک و مکانیک نظری سیالات در جریان نیمه دوم قرن هجدهم و تمام قرن نوزدهم به پیشرفت های بزرگی نایل آمد.نتایج کارهای دانشمندان نامور زمان عبارت بودند از :برنولی که قضیه مهمی را بیان داشت که بر جریان شاره های غیر قابل تراکم حاکم است و بعدا به قضیه ی برنولی معروف شد.اویلر که به مطالعه ی هیدرودینامیک علاقه مند شد و بدین طریق توانست چندین قانون بنیادی مکانیک سیالات را اثبات کند و همچنین اوست که نظریه ی مقاومت سیال را روی جسم در حال حرکت بر اساس فشار بیان داشت.لاپلاس فرمول درست سرعت انتشار صوت در هوا را پیدا و ثابت کرد که سرعت صوت در هوا با جذر دمای مطلق هوا متناسب است.در جریان قرن نوزدهم برای اولین بار پرتابه ها وارد توپخانه ها شدند وبدین سان مطالعه روی پدیده های فراصوتی آغاز شد.آزمونهای تیراندازی بویژه در فرانسه تا سرعتهای حدود 1500 متربر ثانیه انجام میگرفت.در جریان همین آزمایشها بود که ماخ _فیزیکدان اتریشی_در جسمی که با سرعت فرا صوت حرکت میکرد موجهای شوک را کشف کرد.روش استریوسکوپی مشاهده جریانهای فراصوتی که ماخ آن را ابداع هنوز هم مورد استفاده است .حدود قرن اخیر اندیشه ی ساخت هواپیماهای دقیقتر مطرح شد و ماکتهای اولیه ی هواپیما بیشتر مدیون مطالعه روی پرواز پرندگان است.جورج کیلی پروفیلی طراحی کرد که شاید اولین پروفیل بال از روی آن ساخته شده باشد و شکل آن بر اساس برش عرضی ماهی قزل آلا طراحی شده بود.به موازات این کوششهای نظری نخستین دستگاه های آزمایشهای آیرودینامیکی ساخته و بکار گرفته شد .در سال 1871 ونهام ودر سال 1891 فیلیپ در انگلیس اتاقهای دمش را ساختند.بعدا ...
آیرودینامیک

از کوششهای اولیه روی پرواز در زمانهای قدیم که بیشتر بر باورهای افسانه ای پا گرفته اند تا دانش هر چند نااستوار آیرودینامیک بدون توقف می گذریم.در واقع اولین تعریفهای مفید برای آگاهی از قوانین حاکم بر حرکت جسم در شاره در سده ی شانزدهم به هنگام پایه گذاری مکانیک بیان شد.گالیله اولین کسی است که در جریان مطالعه ی حرکت آونگ به مقاومت هوا پی برد. او متوجه شد که حرکت آونگ بتدریج کند می شود و کوشید رابطه ی بین سرعت و مقاومت هوا راتعین کند. آزمایش گالیله عبارت بود از دو آونگ همانند که از دو کره ی با وزن یکسان آویزان از نخهای با طول برابر تشکیل میشدند.یکی را به اندازه ی 10 درجه و دیگری را به اندازه ی 160 درجه از وضع قائم منحرف و سپس رها کرد.بعد از مدت معینی تعداد نوسانهایی که آونگها انجام داده بودند با هم برابر بود.گالیله با توجه به نسبت سرعتها 1 و 16 فکر کرد مقاومت هوا با سرعت متناسب است .اما تنها نیوتن بود که قانون تناسب مقاومت هوا با مجذور سرعت مجذور ابعاد خطی جسم و چگالی هوا را بیان کرد.به علاوه این دانشمند انگلیسی اساس کار اتاق دمش را ریخت که سه قرن بعد تحقق یافت.بعدها برای سرعتهای بالاتر نادرستی متناسب بودن مقاومت هوا با مجذور سرعت به اثبات رسید.در واقع آزمایشهای حرکتهای پرتابی نشان داد که مقاومت هوا در مقابل پیشروی پرتابه ها خیلی بیش از مجذور سرعت افزایش می یابد .از همان هنگام کوششهای مربوط به پیشبرد هیدرودینامیک و مکانیک نظری سیالات در جریان نیمه دوم قرن هجدهم و تمام قرن نوزدهم به پیشرفت های بزرگی نایل آمد.نتایج کارهای دانشمندان نامور زمان عبارت بودند از :برنولی که قضیه مهمی را بیان داشت که بر جریان شاره های غیر قابل تراکم حاکم است و بعدا به قضیه ی برنولی معروف شد.اویلر که به مطالعه ی هیدرودینامیک علاقه مند شد و بدین طریق توانست چندین قانون بنیادی مکانیک سیالات را اثبات کند و همچنین اوست که نظریه ی مقاومت سیال را روی جسم در حال حرکت بر اساس فشار بیان داشت.لاپلاس فرمول درست سرعت انتشار صوت در هوا را پیدا و ثابت کرد که سرعت صوت در هوا با جذر دمای مطلق هوا متناسب است.در جریان قرن نوزدهم برای اولین بار پرتابه ها وارد توپخانه ها شدند وبدین سان مطالعه روی پدیده های فراصوتی آغاز شد.آزمونهای تیراندازی بویژه در فرانسه تا سرعتهای حدود 1500 متربر ثانیه انجام میگرفت.در جریان همین آزمایشها بود که ماخ _فیزیکدان اتریشی_در جسمی که با سرعت فرا صوت حرکت میکرد موجهای شوک را کشف کرد.روش استریوسکوپی مشاهده جریانهای فراصوتی که ماخ آن را ابداع هنوز هم مورد استفاده است .حدود قرن اخیر اندیشه ی ساخت هواپیماهای دقیقتر مطرح شد و ...
گزارش کار آز-مکانیک سیالات
گزارش کار آزمایشگاه مکانیک سیالات آزمایش دوم:سرریزها مقدمه: طبق تعريف هر مانعي كه بر سر راه جريان در كانال قرار گيرد و باعث شود تا آب در پشت آن بالا آمده و بر سرعت آب در ضمن عبور از روي آن افزوده شود، سر ريز ناميده مي شود. برای انتقال آب در طبیعت در اغلب موارد از كانالهای باز استفاده می شود كه رودخانه ها , نهرها و كانالهای پیش ساخته نمونه هایی از آنها هستند. برای آگاهی از مقدار آب عبوری در داخل كانالهای باز از وسیله های مختلفی استفاده می شود. یكی از این وسیله ها سرریز است, كه در واقع موانعی هستند كه در مسیر جریان در داخل كانال قرار داده می شوند و آب از روی آنها عبور كرده و ریزش می كند كه به همین علت به آنها سرریز می گویند. سرریز دارای شكلهای مختلفی هستند كه به سرریزهای مثلثی , مستطیلی و ذوزنقه ای می توان اشاره كرد. در این آزمایش از سرریز مستطیلی ومثلثی استفاده می كنیم. هدف: هدف در این آزمایش تعیین رابطه ای تجربی بین ارتفاع آب جمع شده در پشت سرریز ومحاسبه میزان دبی عبوری از روی سرریزهای مثلثی ومستطیلی وتعیین ضریب تخلیه. شرح آزمايش : ابتدا دبی حجمی را با استفاده از میز کار هیدرولیک حجمی اندازه می گیریم.سرريز را بصورت قائم در كانال، بالا دست بحراني خروجي قرار مي دهيم و دستگاه را روشن مي كنيم . ابتدا دبي را كم مي كنيم و سپس در هر مرحله به وسيله شیر خروجی از پمپ دستگاه دبي را به تدريج اضافه یا کم مي كنيم. این کار را یک بار برای سرریز مثلثی ومرحله بعدی برای سرریز مستطیلی با همان دبی انجام می دهیم. ارتفاع آب جمع شده پشت هر سرریز را یادداشت کرده واز ارتفاع خود سرریز کم می کنیم. محاسبه دبي عبوري : همانطور كه قبلاً ذكر شد يكبار دبي واقعي دستگاه به وسيله میز کار هیدرولیک (حجمی) اندازه می گیریم وسپس با استفاده ازفرمول های هر سرریز دبی تئوری را اندازه می گیریم . فرمول مستطیلی: Qt= 2/3 β √2g .h^3/2 فرمول مثلثی: Qt=8/15√2g .h^5/2 tan(Ѳ/2) از موارد مهم كاربرد سر ريزها عبارتند از: اندازه گيري شدت جريان در كانالها، جريان آب روي سر ريز سدها ، مطالعه مقاطع جاده در مواردي كه كالورت ها تحت تاثير جريان سيلاب قرار گرفته. محاسبات دبی مستطیلی: مرحله اول) V=0.003 (m^3) → t=10 (s) → Q=v/t =0.003/10 =0.0003 (m^3/s) 0.105-0.08= 0.025(m) H= Ή-P= B=0.03(m) Qt= 2/3 β √2g .h^3/2 = 0.000350 (m^3/s) جدول1-1 )اطلاعات مربوط به آزمایش اندازه گیری دبی با استفاده از سرریز مستطیلی Cd Qt(m^3/s) H(m) Ή(m) Qe(m^3/s) t (s) V(m^3) 0.857 0.000350 0.025 0.105 0.000300 10 0.003 1 0.677 0.000703 0.040 0.120 0.000467 6.3 0.003 2 0.652 0.000483 0.031 0.111 0.000315 9.5 0.003 3 0.904 0.000250 0.020 0.100 0.000226 13.22 0.003 4 محاسبات دبی مثلثی: مرحله اول) V=0.003 (m^3) → t=10 (s) → Q=v/t =0.003/10 =0.0003 (m^3/s) H= Ή-P=0.105-0.08=0.025(m) Ѳ=90 Qt=8/15√2g .h^5/2 tan(Ѳ/2) =0.000230 (m^3/s) ...
لوله پیتوت چیست ؟ pitot tube
Aircraft Rescue & Fire Fighting لوله ای که فشار کل را اندازه می گیرد، لوله پیتوت نامیده میشود که همراه با فشار استاتيكي برای اندازه گیرسرعت هوایی هواپیما مورد استفاده قرار می گیرد. لوله های پستوت متعددی را می توان جلوی هواپیمای بزرگ مشاهده کرد. یک لوله پیتوت را در زیر یا جلوی بال هواپیمای کوچک دید.در هواپیما وسیله سنجش گري وجود دارد که اتلاف مقادیر اندازه گیری شده توسط این دو وسیله را اندازه گیری ميكند که بر اساس سرعت درجه بندی شده. این وسیله نمایشگر سرعت هوایی(airspeed indicator) است.چون فشار ديناميكي اندازه گیری شده در ارتباط با خصوصیات هوا می باشد، یک تصحیح خطایی توسط خلبان به خاطر کاهش چگالی هوا در ارتفاعات بالاترازسطح دریاانجام میگیرد.لوله پیتوت یکی از دقیق ترین روش های اندازه گیری سرعت می باشد. از لوله های پیتوت ، برای اندازه گیری سرعت و فشارهای موضعی سیال استفاده می شود. هم چنین از آن ها برای اندازه گیری دبی سیالات برای آزمایش ها ، مطالعات تحقیقاتی ، و کاربردهای مشابه استفاده می شود. نوع خاصی از لوله های پیتوت برای اندازه گیری سرعت در هواپیما استفاده می شود. اساسا یک لوله پیتوت با تعیین اختلاف بین فشار کل (هد کل) و یا فشار ضربه ای (Impact Pressure) و فشار استاتیک ، اندازه گیری سرعت و دبی را انجام می دهد. اختلاف فشار های مذکور که فشار سینتیک نامیده می شود ، به وسیله ی رابطه ای که از قانون برنولی بدست می آید با سرعت ارتباط پیدا می کند. پس برای پیدا کردن فشار دینامیکی (جنبشی) و در نتیجه بدست آوردن سرعت در نقطه ی معینی از خطوط جریان سیال ، ضروری است تا اختلاف بین فشار استاتیک و فشار کل (فشار ضربه ای) مشخص شود. فشار کل به وسیله ی لوله ی فشار کل یا لوله ی فشار (Pressure Tube) اندازه گرفته می شود. لوله ی فشار به صورتی نصب می شود که سطح دهانه ی آن روبروی خطوط جریان سیال قرار گیرد و فشار استاتیک به وسیله ی یک یا چند مجرا که در جداره ی لوله عبور سیال تعبیه شده اندازه گیری می شود. از آن جایی که سرعت سیال در یک نقطه ی معین با استفاده از اختلاف فشار (Pt - Ps) بدست می آید ، در سر لوله های حس کننده فشار کل و استاتیک باید به یک ستون مایع فشار پایین (Liquid-Column Low Pressure) و یا به یک مانومتر اختلاف فشارسنج متصل گردند. برای این کار میزان بالا رفتن سطح مایع ، تحت تاثیر نیروی وارده از سیال تعیین می شود. در رابطه ی برنولی یک پارامتر مربوط به دانسیته ی سیال جاری در لوله و یک پارامتر مربوط به دانسیته ی سیال مانومتر است ، بنابراین برای بالا رفتن دقت محاسبات تا آن جایی که ممکن است ، دانسیته ی هر دو سیال باید دقیق تعیین گردد. نوع پیچیده تری از ...
آمار و احتمالات مهندسی

جزوه ی آمار و احتمالات مهندسی مربوط به دانشگاه علم و صنعت بسیار کامل و تایپ شده که شامل مثال های زیادی می باشد و می توان گفت جزو کامل ترین جزوات موجود در اینترنت است . جزوه موجود شامل 174 صفحه است و شامل سرفصل های زیر است : فصل اول: آمار توصیفی مقدمه تعاریف اولیه فراوانی فراوانی نسبی فروانی تجمعی نسبی جدول آماری جدول فراوانی برای دادههای گسسته جدول فراوانی برای دادههای پیوسته نمودارهای آماری نمودارهای آماری برای دادههای گسسته نمودارهای میلهای نمودارهای دایرهای نمودارهای آماری برای دادههای پیوسته هیستوگرام (نمودار ستونی) چند برابر فراوانی منحنی فراوانی پارامترهای مرکزی و پراکندگی پارامترهای مرکزی میانگین میانه مد یا نما چولگی توزیع فروانی مقدار عدم تقارن یا ضریب چولگی ضریب کشیدگی ادامهی فصل اول پارامترهای پراکندگی دامنهی دادهها میانگین انحرافات واریانس و انحراف استاندارد ضریب تغییرات تغییر مقیاس و مبدا تغییر مقیاس استاندارد سازی تغییر مبدا استاندارد سازی مسائل فصل اول فصل دوم: آنالیز ترکیبی و احتمال آنالیز ترکیبی جایگشت ترکیبهای n شی به گروههای rتایی ترکیب و مسایل انتخاب فضای نمونه و پیشامد انواع پیشامدها و اعمال روی پیشامدها احتمال قوانین احتمال احتمال روی فضای نمونهی نامتناهی فضای نمونهی پیوسته احتمال شرطی قانون ضرب احتمال پیشامدهای مستقل فرمول احتمال بینر و فرمول تفکیک احتمال فصل سوم: متغیرهای تصادفی و توابع توزیع تعریف متغیر تصادفی انواع متغیرهای تصادفی توابع توزیع و چگالی برای متغیرهای تصادفی گسسته خواص توابع توزیع توابع چگالی توابع توزیع و چگالی برای متغیرهای تصادفی پیوسته فصل چهارم: امید ریاضی امیدریاضی برخی از خواص امید ریاضی امید ریاضی تابعی از یک متغیر تصادفی گشتاورها تابع مولد گشتاور امیدریاضی برای متغیر تصادفی پیوسته فصل پنجم: متغیرهای تصادفی دو و چندبعدی متغیرهای تصادفی دو و چندبعدی تابع توزیع دومتغیره امیدریاضی و گشتاورها برای توابع چگالی دومتغیره کوواریانس یا همپراشی ضریب همبستگی خطی بین X و Y فصل ششم: برخی توابع توزیع گسسته برخی توابع توزیع گسسته متغیر تصادفی برنولی و دوجملهای متغیر تصادفی دو جملهای مد توزیع دوجملهای متغیر تصادفی هندسی (نوع اول) متغیر تصادفی هندسی (نوع دوم) متغیر تصادفی دوجملهای منفی (نوع اول) متغیر تصادفی دوجملهای منفی (نوع دوم) متغیر تصادفی فوق هندسی تقریب توزیع فوق هندسی به وسیلهی توزیع دوجملهای متغیر تصادفی پواسن مد توزیع پواسن تقریب توزیع ...
حساب تغییرات بدون در نظر گرفتن شرایط فرعی (معادله اویلر)
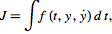
یکی از شاخه های وسیع ریاضیات، نوع خاصی از تعمیم حساب در آن است. حساب تغییرات (وردشها) در جستجوی یافتن مجموعه ای از مسیرها، خم ها، خمینه ها و ... است که به عنوان توابعی پیوسته و مشتق پذیر دارای اکسترم طولی هستند (که اغلب در مسائل فیزیکی از آن به عنوان کمینه یا بیشینه نیز یاد می شود). در ریاضیات، مقدار این اکسترمم بوسیله ی انتگرال معین زیر نمایش داده می شود: که در آن در مسئله ی کوتاه ترین خم زمانی (brachystochrone problem) که توسط یوهان برنولی (Johann BERNOULLI) به سال ۱۶۹۶ علناْ مطرح شد یافتن y ای در انتگرال فوق مطرح است که در آن بتوانیم تعریف ذیل را نمایان سازیم: اگر دو نقطه ی p1 و p2 در ارتفاعات متفاوت اما نه واقع بر بالای یکدیگر، مفروض باشند، می خواهیم از جمیع خم های ممکن واصل آنها، خمی را بیابیم که یک نقطه ی مادی (material point) از p1 به p2 در امتداد آن و تحت تاثیر گرانی یا ثقل (صرفنظر از اصطکاک) در کوتاهترین زمان ممکن بلغزد. مسئله ی فوق در آن زمان، ذهن ریاضیدانان پیشرو تمام اروپا، از قبیل: نیوتون، لایب نیتز، یاکوب برنولی، لوپیتال، هود (HUDDE)، فاتیو (FATIO) و ... را به خود مشغول کرد. از این زمان به بعد حساب تغییرات به عنوان عنوان دستگاه ریاضی خاصی توسعه یافته است. مسئله ی بالا منجر به پیدایش تابع (y(x ای شد که بازای آن مقدار اکسترمم را برای تابع f مطرح کردیم. اما تابع لازم در این مسئله نوع خاصی از جوابی بود که باید در یک معادله ی دیفرانسیل کلی ترصادق باشد. اویلر به همراه لاگرانژ در تحویل مسئله ی تغییرات به معادلات دیفرانسیل توفیق یافت. معادله ی اویلر ـ لاگرانژ (Euler-Lagrange differential equation) یکی از فرمول های بنیادی حساب تغییرات یا وردش هاست. وقتی در انتگرال اول مقدار ثابتی داشته باشد، در این صورت می گوییم معادله ی اویلر ـ لاگرانژ برقرار است. اگر مشتق نسبت به مولفه ی زمانی تابع y یعنی را با مشتق مکانی تعویض کنیم، معادله به شکل زیر تبدیل خواهد شد: در بسیاری از مسائل فیزیکی، (مشتق جزئی نسبت به ) معلوم می شود که برابر صفر است، بنابراین در موارد خاصی از این قبیل معادله ی اویلر به معادله ی ساده شده و دارای شکل انتگرالی می انجامد که به اتحاد بلترامی (Beltrami identity) موسوم است: برای سه متغیر مستقل (Arfken 1985, pp. 924-944) رابطه ی اویلر به شکل زیر تعمیم می یابد: مسائلی که در حساب تغییرات مطرح می شود، اغلب با معادله ی اویلر به سادگی قابل حل هستند. برای اثبات این معادله، ابتدا مشتق انتگرال اکسترمم را با شرایط زیر و نسبت به q در نظر ...
