آموزش کامل انتگرال
آموزش کامل انتگرال
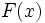
انتگرال نامعین اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه: نکته اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد. انتگرال نامعین مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند. هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم : تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است. خواص انتگرال انتگرال مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه. یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.) انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد. فرمول های انتگرال گیری , , , , در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است. اگر آنگاه انتخاب مقدار ثابت انتگرالگیری در حل یک معادله دیفرانسیل مانند معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از را تعیین میکنیم که جواب خاص مطلوب را به دست دهد. اگر نقطهای چون از دامنه را در نظر بگیریم و مقدار دلخواه را برگزینیم ، میتوان با قرار دادن و در معادله و حل آن نسبت به جوابی را یافت که از نقطه بگذرد.به این ترتیب داریم یا . خم خمی است که از میگذرد. انتگرالگیری به کمک تغییر متغیر در حل انتگرالها با روش تغییر متغیر ، به جای تابع پیوسته و مشتق پذیر را قرار می دهیم، یعنی : بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار میدهیم . یعنی: از فرمول فوق به صورت زیر هم میتوان استفاده کرد: انتگرالگیری به روش جزء به جزء دستور موسوم به انتگرالگیری به روش جزء به جزء است که در آن توابعی مشتقپذیر از هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب میکنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را فرض میکنند. دید کلی برای آنکه بتوانیم مساحت شکل مسطح را حساب کنیم واحدی برای مساحت در نظر میگیریم که عبارت است ...
آموزش کامل انتگرال
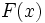
انتگرال نامعین اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه: نکته اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد. انتگرال نامعین مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند. هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم : تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است. خواص انتگرال انتگرال مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه. یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.) انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد. فرمول های انتگرال گیری , , , , در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است. اگر آنگاه انتخاب مقدار ثابت انتگرالگیری در حل یک معادله دیفرانسیل مانند معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از را تعیین میکنیم که جواب خاص مطلوب را به دست دهد. اگر نقطهای چون از دامنه را در نظر بگیریم و مقدار دلخواه را برگزینیم ، میتوان با قرار دادن و در معادله و حل آن نسبت به جوابی را یافت که از نقطه بگذرد.به این ترتیب داریم یا . خم خمی است که از میگذرد. انتگرالگیری به کمک تغییر متغیر در حل انتگرالها با روش تغییر متغیر ، به جای تابع پیوسته و مشتق پذیر را قرار می دهیم، یعنی : بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار میدهیم . یعنی: از فرمول فوق به صورت زیر هم میتوان استفاده کرد: انتگرالگیری به روش جزء به جزء دستور موسوم به انتگرالگیری به روش جزء به جزء است که در آن توابعی مشتقپذیر از هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب میکنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را فرض میکنند. دید کلی برای آنکه بتوانیم مساحت شکل مسطح را حساب کنیم واحدی برای مساحت در نظر میگیریم که عبارت است از مساحت ...
مرجع کامل فرمول های انتگرال
فرض کنید f تابعی پیوسته باشد در این صورت انتگرال تابع f به صورت زیر تعریف می شود . در وضع انتگرال عکس مشتق است بنابراین می توان گفت : برخی از فرمول های انتگرال:برای مشاهده تمام فرمولها یه سر به ادامه مطلب بزنید.
آموزش انتگرال به همراه فرمولهای انتگرال
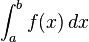
انتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد. اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد نمايش مي دهند. بنا به تعريف نماد را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: با شرط: (F(x) + c)' = f(x) انتگرال معين بنا به تعريف نماد را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار. نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است. انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم: بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از : انتگرال گيري بهوسيله تغيير متغير انتگرال گيري جزء به جزء : انتگرال گيري ...
آموزش تصویری انتگرال
درس های آمار و احتمال مهندسی و معادلات دیفرانسیل نیاز اساسی به یادگیری انتگرال دارن!!این دوره ها توسط (آقای وجدانی درستکار) آموزش داده شده اند که برای شروع کار خیلی مفید هستش.مجموعه ی کامل انتگرال در سایت ایشون برای فروش گذاشته شده که احتمالا در حدود 60 کلیپ باشه اما ما در اینجا در حدود 16 تای اونها رو در اختیار داریم!!مقدمات انتگرال:دریافت کلیپ های(1و2و3)انتگرال های جبری:دریافت کلیپ های(4و5و6)انتگرال های مثلثاتی:دریافت کلیپ های(7و8و9)انتگرال گیری از توان های زوج و فرد سینوس و کسینوس:دریافت کلیپ های(10و11و12)چندتای دیگر از این کلیپ ها:دریافت...
دانلود حل المسائل کامل درس حساب دیفرانسیل و انتگرال جدید التالیف (۱۳۹۱)
دانلود حل المسائل کامل درس حساب دیفرانسیل و انتگرال جدید التالیف (۱۳۹۱) حل کامل تمرین در کلاس ها و مسائل کتاب حساب دیفرانسیل و انتگرال دوره پیش دانشگاهی ریاضی، که توسط استاد پرویز رضایی مدرس دوره ضمن خدمت دروس ریاضی۱و۲ ، حسابان و حساب دیفرانسیل و انتگرال (استان فارس) تهیه و به سایت ریاضی سرا ارسال گردیده را از لینک های زیر دانلود نمایید. با تشکر فراوان از استاد رضایی حل المسائل فصل های صفر و یک کتاب دیفرانسیل حجم فایل : 2.7 مگابایت لینک دانلود: لینک دانلود | لینک کمکی حل المسائل فصل دوم کتاب دیفرانسیل حجم فایل : 4.2 مگابایت لینک دانلود: لینک دانلود | لینک کمکی حل المسائل فصل سوم کتاب دیفرانسیل حجم فایل : 4.3 مگابایت لینک دانلود: لینک دانلود | لینک کمکی حل المسائل فصل چهارم کتاب دیفرانسیل حجم فایل: 3.1 مگابایت لینک دانلود: لینک دانلود | لینک کمکی
دانلود جزوه کامل و جامع آموزش کتاب حساب دیفرانسیل و انتگرال جدید
دانلود جزوه کامل و جامع آموزش کتاب حساب دیفرانسیل و انتگرال جدید علاقه مندان مي توانند جزوه ي درسي حساب ديفرانسيل و انتگرال سال چهارم رشته ي رياضي را از قسمت پایین دريافت نمايند این جزوه شامل فصول:دستگاه اعداد---دنباله و سری---حد و پیوستگی---مشتق---کاربرد مشتق---انتگرال و کاربرد آن کاری از استاد بزرگوار و دبیر نمونه کشوری آقای جابر عامری حجم :۳ مگابایت دانلود : لینک مستقیم | پیکو فایل رمز فایل : www.fera.ir منبع : دبیرستانی کنکوری استفاده از مطالب اين سايت با ذکر منبع و لينک سايت بلامانع مي باشد
جدول کامل فرمول های انتگرال
جدول کامل فرمول های انتگرال ( عمومي ) جدول کامل فرمول های انتگرال :Rules for integration of general functionsRational functionsIrrational functionsLogarithmsExponential functionsTrigonometric functionsHyperbolic functionsInverse hyperbolic functionsDefinite integrals lacking closed-form antiderivatives (if n is an even integer and ) (if is an odd integer and ) (,
دانلود جزوه کامل و جامع آموزش کتاب حساب دیفرانسیل و انتگرال جدید
علاقه مندان مي توانند جزوه ي درسي حساب ديفرانسيل و انتگرال سال چهارم رشته ي رياضي را از قسمت پایین دريافت نمايند این جزوه شامل فصول:دستگاه اعداد---دنباله و سری---حد و پیوستگی---مشتق---کاربرد مشتق---انتگرال و کاربرد آن کاری از استاد بزرگوار و دبیر نمونه کشوری آقای جابر عامری حجم :۳ مگابایت دانلود :پیکو فایل رمز فایل : www.fera.ir منبع : دبیرستانی کنکوری
دانلود کتاب حل کامل مسائل حساب دیفرانسیل و انتگرال

دانلود کتاب حل کامل مسائل حساب دیفرانسیل و انتگرال دانلود کتاب حل کامل مسائل حساب دیفرانسیل و انتگرالتالیف ناصر رضائی ایوبمطابق با کتاب دیفرانسیل چاپ جدید پاسخ به سوالات دروس ریاضیات شما در تاپیک ریاضیات انجمن کنکور نام فایل : حل کامل مسائل حساب دیفرانسیل و انتگرالحجم : 13.63 مگابایتدانلود : لینک مستقیم رمز فایل : www.konkur.in منبع : سایت کنکور
