نسبیت خاص

لبته در نظر داشته باشید که هنگامی که c به سمت بی نهایت میل می کند( همانگونه که پیش از اثبات متناهی بودن سرعت نور پنداشته می شد) کسر v/c به سمت صفر می‌رود. این بدان معناست که تبدیلات لورنتس که اساس نظریهٔ نسبیت خاص هستند در سرعت‌های بسیار کم نسبت به نور، نتایج یکسانی را با معادلات گالیله که اساس نسبیت نیوتونی هستند به دست می‌دهند. نظریه نسبیت خاص به ما می گوید که c تنها سرعت یک پدیده مشخص نیست بلکه یکی از ویژگیهای بنیادی شیوه ای است که فضا و زمان با یکدیگر به شکل فضا زمان یکپارچه گشته اند. یکی از پیامدهای این نظریه است که ذره ای که جرم لختی دارد هرگز سرعتش به سرعت نور نمی رسد.

واژه خاص در نسبیت خاص به نشانگر حالت خاصی است که این نظریه در آن صادق است.این نظریه اصل نسبیت را تنها در مورد ویژه چارچوبهای مرجع لخت به کار برده است. به عبارت دیگر این طور پنداشته شده است که چارچوبهای مرجع نسبت به یکدیگر با سرعت یکنواختی حرکت می کنند. انیشتین نسبیت عام را معرفی نمود و اصل نسبیت را در حالت کلی تری به کارگرفت تا برای هر چارچوبی که قادر به تغییر مختصات عمومی است، صادق باشد. این نظریه تاثیرات گرانشی را هم در نظر می گیرد.

این واژه امروزه کاربرد کلی تری پیدا کرده و برای ارجاع به هر موردی که در آن گرانش ناچیز است استفاده می شود. نسبیت عام تعمیمی بر نسبیت خاص است که گرانش را نادیده نمی گیرد. در نسبیت عام گرانش توسط هندسه نااقلیدسی توصیف می شود؛ به گونه ای که تاثیرات گرانشی با خمش فضازمان نمایش داده می شوند. نسبیت خاص تنهابه فضاهای تخت محدود است. همانگونه که خمش زمین در زندگی روزمره ناچیز به نظر می رسد خمش فضازمان نیز در مقیاسهای کوچک قابل صرف نظر کردن است و بنا بر این به صورت محلی نسبیت خاص تقریب قابل قبولی از نسبیت عام است.

چارچوب های مرجع، مختصات ها و تبدیلات لورنتس

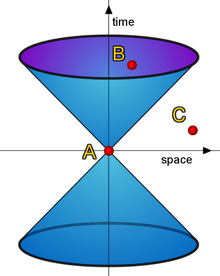
ترسیمی از یک مخروط نوری نوشتار اصلی: تبدیلات لورنتس

نسبیت بر پایه مفهوم "چارچوب های مرجع" استوار است. در اینجا منظور از واژه چارچوب مرجع، یک ژرفانمایی(پرسپکتیو) مشاهده ای در فضاست که تغییری در حرکت آن رخ نمی دهد(شتاب ندارد) که از طریق آن می توان یک موقعیت را در امتداد سه محور فضایی اندازه گرفت. افزون براین یک چارچوب مرجع توانایی تعیین زمان رویدادها از طریق یک 'ساعت'(هر دستگاه مرجعی با تناوب یکنواخت) را دارد.

یک رویداد اتفاقی است که می توان یک زمان یکتا و مکانی در فضا نسبت به یک چارچوب مرجع نسبت داد: "نقطه" ای در فضازمان . از آنجاییکه سرعت نور در نسبیت در همه چارچوبهای مرجع ثابت است، می توان از پالس های نور برای اندازه گیری مطمئن فاصله ها و ارجاع به زمانهای که رویدادها برای ساعت اتفاق افتاده اند استفاده نمود. اگرچه که برای نور هم زمانی پس از شروع رویداد طول خواهد کشید تا به ساعت برسد.

مثلا انفجار یک ترقه را می توان یک "رویداد" در نظرگرفت. می توان یک رویداد را به طور با استفاده از چهار مختصات فضازمان آن مشخص نمود. زمان رویداد و مکان فضایی سه بعدی اش یک نقطه مرجع می سازند.این چارچوب مرجع را S می نامیم. در نسبیت اعلب اغلب به محاسبه موقعیت یک نقطه از یک نقطه مرجع دیگ علاقه مندیم. فرض کنید که چارچوب مرجع دومی به نام ′S داریم که محورهای فضایی و ساعتش با محورهای فضایی و ساعت S در زمان صفر همزمان و هم مکان بوده اند، اما با سرعت ثابت v نسبت به S در امتداد محور ایکس ها حرکت می کند.

از آنجا که در نظریه نسبیت هیچ چارچوب مرجع مطلقی وجود ندارد، مفهوم موکدی از "حرکت" نیز وجود ندارد زیرا همه چیز همواره نسبت به چارچوب مرجع دیگری در حرکت است. به جای آن هرگاه دو چارچوب مرجع که باسرعت یکسان در جهت یکسان حرکت کنند، به آن حرکت همراه گفته می شود. بنا براین S و′S حرکت همراه ندارند. برای رویدادها مختصات فضازمان(t,x,y,z) در دستگاه S و (t′,x′,y′,z′) در دستگاه ′S تعریف می کنیم. تبدیل لورنتس بیان می کند که این دو مختصات به شیوه زیر در ارتباط هستند:

$\begin{cases} x' = \gamma \left( x - v t \right)\\ y' = y \\ z' = z \\ t' = \gamma \left( t - \frac{v x}{c^{2}} \right) \end{cases}$

که در آن $\gamma = { 1 \over \sqrt{1 - \beta^2} }$ را فاکتور لورنتس می نامند و $\beta = \frac{v}{c}$ . c سرعت نور در خلا است و وسرعت v دستگاه ′S در راستای محور xهاست.مختصات y,z تغییری نمی کنند و تنها مختصات x , t تبدیل می شوند. این تبدیلات لورنتس یک گروه تک پارامتر از نگاشت های خطی تشکیل می دهند که به آن پارامتر تندی (به انگلیسی: rapidity)‏ می گویند.کمیتی که نسبت به تبدیلات لورنتس ناوردا باشد را کمیت نرده ای لورنتس می نامند.

چنانچه تبدیلات لورنتس و معکوسشان را برحسب اختلاف مختصاتها بنویسیم به گونه ای که مثلا مختصات یک رویداد (x1, t1) and (x′1, t′1) باشد، مختصات رویداد دیگر (x2, t2) خوهد بود و (x′2, t′2) و اختلافها را به صورت زیر تعریف کنیم

$\begin{array}{ll} \Delta x' = x'_2-x'_1 \ , & \Delta x = x_2-x_1 \ , \\ \Delta t' = t'_2-t'_1 \ , & \Delta t = t_2-t_1 \ , \\ \end{array}$

به روابط زیر می رسیم

$\begin{array}{ll} \Delta x' = \gamma (\Delta x - v \,\Delta t) \ , & \Delta x = \gamma (\Delta x' + v \,\Delta t') \ , \\ \Delta t' = \gamma \left(\Delta t - \dfrac{v \,\Delta x}{c^{2}} \right) \ , & \Delta t = \gamma \left(\Delta t' + \dfrac{v \,\Delta x'}{c^{2}} \right) \ . \\ \end{array}$

تبدیلات لورنتس که توسط ریاضیدان و فیزیکدان آلمانی هندریک لورنتس با استفاده از روابط هندسی و دو فرض همسانگرد و همگن بودن فضا برای توجیه نظریهٔ اتر به دست آمد اساس نظریهٔ نسبیت خاص می‌باشد. همسانگرد بودن فضا بدین معناست که خواص آن در تمامی جهات یکسان است. همگن بودن فضا بدین معناست که خواص فضا به نقطه‌ای که شما در آن قرار دارید بستگی ندارد. فرض همسانگرد بودن فضا به ما اجازه می‌دهد که بتوانیم حرکت ذره را در راستای محور xها بررسی کنیم( یعنی از راستاهای y و z برای خلاصه سازی چشم پوشی کنیم )، فرض همگن بودن فضا تضمین می‌کند که این معادلات حتماً درجه اول هستند، یعنی تنها توان اول متغیرهای ما می‌توانند دخالت داشته باشند.( چون اگر به توان دوم یا درجات بالاتر بستگی داشته باشند اثبات می‌شود که آنگاه طول یک میله بستگی به نقطه‌ای از فضا که میله در آن قرار گرفته است دارد، یعنی مثلاً یک میله که بدون حرکت در ارتفاع 5 متری قرار دارد با هنگامی که همان میله بدون حرکت در ارتفاع 3 متری قرار دارد طول متفاوتی دارد و این خلاف شهود ماست)

نکته جالب توجه این است که این معادلات پیش از چاپ مقالهٔ آلبرت انیشتین در رابطه با الکترودینامیک دراجسام متحرک به دست آمده بود اما فرض وجود اتر و فضایی برای انتشار امواج الکترومغناطیس به قدری قوی بود که این تبدیلات به عنوان تلاشی برای اصلاح آن فرضیه عنوان شد. چند سال بعد انیشتین به گونهٔ دیگری با استفاده از دو پنداشتی که در پیش گفته شد به تبدیلات لورنتس رسید ! همانگونه که خود انیشتین نیز گفته است : " تمامی نتایج نسبیت خاص می‌توانند از تبدیلات لورنتس به دست آیند."

نسبیت خاص

چارچوب های مرجع، مختصات ها و تبدیلات لورنتس

مطالب مشابه :

تبدیلات لورنتس و اثبات کامل

نسبیت خاص

تبدیلات گالیله

Symmetry & similarity