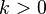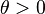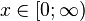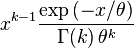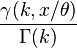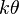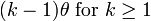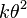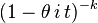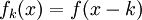توزیع گاما
توزیع گاما یکی از توزیعهای احتمالی پیوسته است و دارای دو پارامتر مقیاس θ، و پارامتر شکل k میباشد. اگر kعددی طبیعی باشد آنگاه توزیع گاما معادل است با مجموع k متغیر تصادفی با توزیع نمایی با پارمتر  .
.
تابع چگالی احتمال:
که در آن 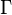 تابع گاما، θ پارامتر مقیاس، و k پارامتر شکل میباشند.
تابع گاما، θ پارامتر مقیاس، و k پارامتر شکل میباشند.
تابع گاما، انتگرالی همگراست و مقدار آن برابر با عددی مثبت است:
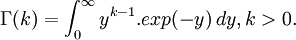
ویژگیها
هرگاه k (پارامتر شکل) یک عدد صحیح و مثبت چون n باشد، میتوان از توزیع گاما برای تخمین زدن مدتزمان لازم برای رویدادن n پیشامد استفاده نمود.
توزیع مجموع
اگر 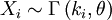 اگر n متغیر دو به دو مستقل از هم باشند، آنگاه:
اگر n متغیر دو به دو مستقل از هم باشند، آنگاه:
در نتیجه توزیع گاما بینهایت تقسیمپذیر است.
توزیعهای مرتبط
هرگاه k=۱ شود، حالت خاصی از توزیع گاما به وجود میآید که توزیع نمایی نامیده میشود.
تابع گاما
تابع گاما تعمیم تابع فاکتوریل است از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی و مختلط و برای یک عدد مختلط با بخش حقیقی مثبت به شکل زیر تعریف میشود:
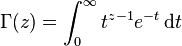
در ضمن برای هر عدد طبیعی z داریم:
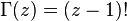
همچنین میتوان ثابت کرد که:
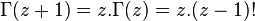
پارامتر مقیاس
اگر بتوان یک خانواده از توزیعهای احتمالی را به کمک پارامتر s به شکل زیر نوشت:
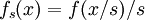
آنگاه پارامتر s را پارامتر مقیاس گویند.
پارامتر شکل
در علم آمار و احتمالات پارامتر شکل به پارامتری گفته میشود که با تغییر آن، شکل تابع توزیع احتمالی تغییر مینماید (مقایسه نمایید با پارامتر مکان و پارامتر مقیاس) . بطور مثال توابع توزیع احتمالی زیر دارای پارامتر شکل میباشند:- توزیع ارلانگ
- توزیع بر
- توزیع بتا
- توزیع توانی نمایی
- توزیع گاما
- توزیع مقدار نهایی تعمیمیافته
- توزیع پارتو
- توزیع پیرسون
- توزیع وایبول
پارامتر مکان
اگر بتوانیم یک خانواده از توزیعهای احتمالی را به کمک پارامتر k به شکل زیر بنویسیم:
آنگاه پارامتر k را پارامتر مکان گوییم.
مطالب مشابه :
روش آزمون توزیع نرمال کولموگراف در SPSS
روش آزمون توزیع نرمال کولموگراف در spss مطلب مصور زیر براحتی این روش را رسم نمودار
توزیع گاما
که تقریبا توزیع نرمال با برای دیدن این مطلب چطوره که نسبت خاصی از تابع گاما در
صد نکته از آمار و احتمال مقدماتی
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
کل آمار مقدماتی در یک صفحه
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
100 نکته آماری
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
آموزش احتمال
تابع توزیع یک متغیر تصادفی چون x به ما توزیع نرمال در نقطه μ=x دارای Max رسم نمودار
بررسی نرمالبودن توزیع٬ آزمون کولوموگراف-اسمیرنوف
بررسی نرمالبودن توزیع٬ آزمون کولوموگراف در آزمون نرمالبودن٬ چنانچه تابع تمایز
صد نکته از آمار و احتمال مقدماتی
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
توزیع گاما
در نتیجه توزیع گاما بی شود که با تغییر آن، شکل تابع توزیع احتمالی رسم نمودار
آموزش مطلب / متلب / Matlab
Index / بردار و رسم منحنی در مطلب/ توابع برنامه در مطلب / تابع Function و توزیع ;
برچسب :
رسم تابع توزیع نرمال در مطلب