مثلث قائم الزاویه و روابط مثلثاتی
 |
تعریف روی مثلث قائم الزاویه
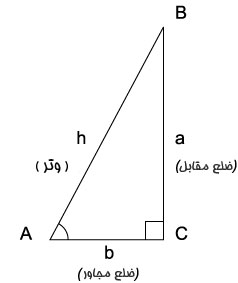
برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه استفاده می کنیم به عنوان مثال می خواهیم این توابع را برای زاویه A در شکل روبرو تعریف کنیم
ما برای استفاده از این مثلث نامگذاری زیر را انجام می دهیم.
وتر ضلعی است که روبروی زاویه قائم قرار دار که بلندترین ضلع مثلث نیز می باشد و آن را با h نشان داده شده است.
ضلع مقابل زاویه A که آن را با a نشان می دهیم.
ضلع مجاور زاویه قائمه که درشکل با b نشان داده شده است.
حال توابع مثلثاتی را برای زاویه A روی مثلث ABC تعریف می کنیم.
- sin: نسبت ضلع مقابل به وتر را سینوس می گویند یعنی:

- cos: نسبت ضلع مجاور به وتر را گویند یعنی داریم:

- tangent: نسبت ضلع مقابل زاویه به ضلع مجاور را گویند.

- cosecant: نسبت وتر به ضلع مقابل زاویه را گویند.

- secant: نسبت وتر به ضلع مجاور است

- cotangent: نسبت ضلع مجاور به ضلع مقابل را گویند.

تعریف روی دایره واحد
 |
در یک صفحه دستگاه مختصات دکارتی، زاویه می تواند هر چهار ربع را طی کند، و مقدار آن می تواند به حسب درجه، گراد رادیان اندازه گیری شود.
ضلع متروک این زاویه، دایره با شعاع و مرکز در مبدا، دایره موسوم به دایره واحد یا یک را در نقطه قطع می کند.
زاویه در تقاطع محور ها با دایره، مقدار صفر را اختیار می کند این زاویه، طی یک دوران کامل ضلع متحرکش حول مبدا از صفحه شروع و پس از رسیدن به مکان اولیه، دارای زاویه 360 درجه می باشد.
روابط مثلثاتی که برای زوایای مختلف برقرار است. برای زوایای بزرگتر از 360 نیز، بر قرار می باشد. مثلا برای دو تابع سینوس و کسینوس خواهیم داشت:


مطالب مشابه :
در این مقاله روشی برای محاسبه ی سینوس زوایای دلخواه ارائه می شود كه به كمك آن
در این مقاله روشی برای محاسبه ی سینوس زوایای های مثلثاتی را اندازه ی خودش تا
توابع مثلثاتی معکوس
منشا توابع مثلثاتی معکوس، مسائلی است که در آن ها باید با استفاده از اندازه ی زوایای متمم
مثلث
ریاضیات دوره ی مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای نسبت های مثلثاتی
مثلث
مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای مثلثاتی مانند sin و اندازه زاویه
جدول مثلثاتی
این وب تقدیم به روح آســمانی پدرم و همه ی پدرانی که یادشان پرچم صلحی ست به جدول مثلثاتی.
زاویه و دایره
کاربرد تکنیک های حافظه برای حفظ سریع فرمول های ریاضی و مثلثاتی اندازه ی زوایای داخلی
روش محاسبه سطح مثلث و اشکال هندسی
مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای نسبت های مثلثاتی قاعده ی منشور
زاویه و دایره
نرم افزار در زمینه رسم معادلات خطی ، توابع مثلثاتی اندازه ی 3 نیمساز زوایای
مثلث قائم الزاویه و روابط مثلثاتی
به حسب درجه، گراد رادیان اندازه مثلثاتی که برای زوایای مختلف دوره ی راهنمایی
برچسب :
اندازه ی زوایای مثلثاتی
