تبدیل فوریه

همانطور که می دانید مهمترین ویژگی در ادای هر حرف فرکانس های تشکیل دهنده آن حرف می باشد. به عنوان مثال سه فرکانس اصلی حرف " آ " فرکانس های 750 ، 1150 و 2400 هرتر بوده و همین فرکانس های برای حرف " او " 400 ، 1150 و 2300 هرتز می باشند. بنابراین آنچه باعث تفکیک دو حرف " آ " و " او " از همدیگر می شود، فرکانس های تشکیل دهنده آن می باشد. از اینرو در کاربردهای پردازش گفتار پیدا کردن فرکانس های تشکیل دهنده یک سیگنال گفتاری از اهمیت بسیار زیادی برخوردار می باشد.

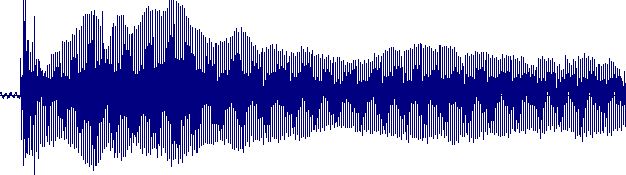
همانطور که می دانید سیگنال گفتار به شکل یک سیگنال زمانی در اختیار ما قرار دارد و تشخیص فرکانس های تشکیل دهنده یک سیگنال در حوزه زمانی غیرممکن است. به عنوان مثال شکل زیر را که نشان دهنده سیگنال گفتار زمانی حرف " آ " می باشد در نظر بگیرید. بخشی از این سیگنال به شکل زوم شده در شکل نشان داده شده است.

از این شکل پیداست که پیدا کردن فرکانس های تشکیل دهنده این سیگنال از روی سیگنال زمانی غیررممکن می باشد. از اینرو نیاز به ابزار دیگری داریم که بتواند این کار را برای ما انجام دهد. آقای فوریه نشان دادند که هر تابع متناوب را می توان به شکل ترکیبی از موج های سینوسی ( یا کوسینوسی ) نشان داد که این مطلب را با نام سری های فوریه می شناسیم. از مقاله مربوطه به موج سینوسی به یاد دارید که هر موج سینوسی می تواند به شکل یک صوت در خروجی بلندگو به شنیده شود. در این بین فرکانس موج سینوسی نیز مستقیما زیر و بم بودن صوت تولید شده را تعیین می کند.

با توجه به این دو حقیقت می توان دریافت که با استفاده از آنالیز فوریه یک سیگنال می توان موج های سینوسی تشکیل دهنده آن را استخراج کرد و از روی موج های سینوسی نیز می توان فرکانس های تشکیل دهنده سیگنال گفتار را به دست آورد. با این حال نمی توان مستقیما از سری های فوریه برای این منظور بهره جست. چراکه سری های فوریه بر روی توابع متناوب تعریف شده اند و این در حالی است که ما در اینجا با سیگنال سروکار داریم که هیچ تابعی را نمی توان برای یک سیگنال گفتار تخمین زد. برای رفع این مشکل ابزاری با نام تبدیل فوریه معرفی شده است که بر روی داده های عددی ( سیگنال ) اعمال می شود. تبدیل فوریه گسسته مختلط سیگنال s به طول N را می توان با استفاده از رابطه زیر تعریف کرد:

از قانون اویلر نیز به یاد دارید که :

بنابراین رابطه فوق را می توان به شکل زیر بازنویسی کرد :

که در این رابطه N اندازه سیگنال ورودی ، s(n) مقدار سیگنال ورودی در نقطه n ، m اندیس فرکانس، S(m) اندازه فرکانس در اندیس m ام می باشند. همانطور که می دانید S(m) یک عدد مختلط است و بنابراین برای به دست اندازه فرکانس در اندیس mام باید بزرگی این عدد مختلط را محاسبه کرد. بزرگی یک عدد مختلط از رابطه زیر به دست می آید :

پس از آنکه تبدیل فوریه بر روی سیگنال ورودی اعمال شد، بردار S در فرکانس های تشکیل دهنده سیگنال s دارای مقداری بسیار بزرگتر از 0 و در سایر نقاط بزرگی نزدیک به صفر خواهد داشت. بنابراین می توان برای پیدا کردن فرکانس های تشکیل دهنده یک سیگنال گفتار تبدیل فوریه را بر روی سیگنال ورودی اعالم کرده و پس از محاسبه بزرگی خروجی، فرکانس های تشکیل دهنده آن سیگنال را از روی بزرگی هر فرکانس استخراج کرد. در مقاله بعدی سعی می کنیم این مساله را به همراه سایر پارامترها و خصوصیات سیگنال گفتار مورد بررسی قرار دهیم. برای محاسبه تبدیل فوریه یک سیگنال در محیط MATLAB از تابع fft می توانید استفاده کنید:

>> a = sin(2*pi * 200/1000 * t);
>> b = sin(2*pi * 10/1000 * t);
>> c = sin(2*pi * 500/1000 * t);
>> d = a + b + c;
>> ffd = fft(d);
>> mffd = abs(ffd);
>> plot(mffd(1:500))

در این تکه کد ابتدا سه موج سینوسی با فرکانس های 20، 10 و 500 هرتز تولید کرده و پس از ترکیب آن ها سیگنال جدیدی با نام d به وجود آوردیم. سپس با استفاده از تابع fft تبدیل فوریه سیگنال d را محاسبه کرده و با استفاده از تابع abs بزرگی سیگنال تبدیل شده را به دست آوردیم. در نهایت نیز به رسم سیگنال تبدیل شده پرداختیم.

در نموداری که پس از فراخوانی دستور plot برای شما نشان داده می شود، در نقاط 10 ، 200 و 500 نمودار دارای مقدار بزرگ بوده و در سایر نقاط دارای مقدار صفر است. این نشان می دهد که سیگنال d شامل فرکانس های 10 ، 200 و 500 هرتز می باشد.

mathworks.ir

تبدیل فوریه

مطالب مشابه :