بررسی نرمالبودن توزیع٬ آزمون کولوموگراف-اسمیرنوف
۱. هدف آزمون برای انتخاب آزمون درست برای تحلیل فرضیهها٬ ابتدا باید از توزیع آماری متغیری که مورد آزمون قرار میگیرد٬ اطمینان حاصل کرد. برای نمونه٬ پیشنیاز گرفتن آزمونهای پارامتری٬ نرمالبودن توزیع آماری متغیرهاست. به طور کلی میتوان گفت که آزمونهای پارامتری، عموما بر میانگین و انحراف معیار استوارند. حال اگر توزیع جامعه نرمال نباشد، نمیتوان استنباط درست از نتایج داشت.
برای بررسی توزیع آماری متغیرها از آزمونهایی استفاده میکنند. این آزمونها به آزمونهای نیکویی-برازش معروفند. آزمون کولوموگراف اسمیرنوف به همراه آزمون کای دو٬ جزو آزمونهای نیکویی- برازش هستند. اما با توجه به محدودیتهای آزمون کایدو٬ معمولا برای آزمون نرمالبودن٬ از آزمون کولوموگراف-اسمیرنوف استفاده میشود... .
در این آزمون ، میتوانید متغیر خود را بر مبنای این توزیعها تست کنید
- Normal نرمال
- Poisson پواسون
- Uniform یکنواخت
- Exponential نمایی
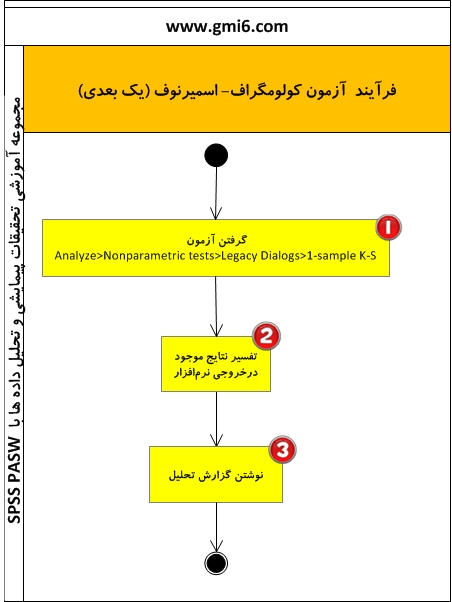
۲.تحلیل نتایح
با انجام این آزمون٬ نرمافزار یک عدد معنیداری محاسبه میکند. در آزمون نرمالبودن٬ چنانچه معنیداری (Sig) بيشتر از ۵ درصد یا ۵ صدم بود٬ نرمالبودن توزیع نتیجه گرفته میشود. باید به یاد داشت که آزمون کولموگراف-اسمیرنوف یک آزمون دو دنباله میباشد و برای تفسیر بهتر است اینگونه بیان شود که عدد معنیداری بر ۲ تقسیم شده است و چنانچه این عدد بيشتر از ۲.۵ درصد یا ۲۵ هزارم باشد٬ توزیع نرمال است.
مطالب مشابه :
روش آزمون توزیع نرمال کولموگراف در SPSS
روش آزمون توزیع نرمال کولموگراف در spss مطلب مصور زیر براحتی این روش را رسم نمودار
توزیع گاما
که تقریبا توزیع نرمال با برای دیدن این مطلب چطوره که نسبت خاصی از تابع گاما در
صد نکته از آمار و احتمال مقدماتی
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
کل آمار مقدماتی در یک صفحه
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
100 نکته آماری
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
آموزش احتمال
تابع توزیع یک متغیر تصادفی چون x به ما توزیع نرمال در نقطه μ=x دارای Max رسم نمودار
بررسی نرمالبودن توزیع٬ آزمون کولوموگراف-اسمیرنوف
بررسی نرمالبودن توزیع٬ آزمون کولوموگراف در آزمون نرمالبودن٬ چنانچه تابع تمایز
صد نکته از آمار و احتمال مقدماتی
42 تغییر میانگین به یک مقدار بیشتر در توزیع نرمال سبب y ها رسم کنیم از تابع توزیع
توزیع گاما
در نتیجه توزیع گاما بی شود که با تغییر آن، شکل تابع توزیع احتمالی رسم نمودار
آموزش مطلب / متلب / Matlab
Index / بردار و رسم منحنی در مطلب/ توابع برنامه در مطلب / تابع Function و توزیع ;
برچسب :
رسم تابع توزیع نرمال در مطلب
