آموزش انتگرالها

در حساب دیفرانسیل و انتگرال ، از انتگرال یک تابع برای عمومیت دادن به محاسبه مساحت ، حجم ، جرم یک تابع استفاده می شود. فرایند پیدا کردن جواب انتگرال را انتگرال گیری گویند.البته تعاریف متعددی برای انتگرال گیری وجود دارد ولی در هر حال جواب مشابه ای از این تعاریف بدست می آید. انتگرال یک تابع مثبت پیوسته در بازه (a,b) در واقع پیدا کردن مساحت بین خطوط x=0 , x=10 و خم منفی F است . پس انتگرال F بین a و b در واقع مساحت زیر نمودار است. اولین بار لایب نیتس نماد استانداری برای انتگرال معرفی کرد و به عنوان مثال انتگرال f بین a و b رابه صورت 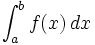نشان می دهند علامت ،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری است.

img/daneshnameh_up/9/96/graph_integral1-1.jpg

انتگرال یک تابع مساحت زیر نمودار آن تابع است.

از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی
پایه گذاری شده است به عنوان مثال تابع f را بین x=0 تا x=10 در نظر بگیرید ،مساحت زیر نمودار در واقع مساحت مستطیل خواهدبود که بین x=0 ،x=10 ،y=0 ،y=3 محصور شده است یعنی دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود .

اگر تابعی دارای انتگرال باشد به آن انتگرال پذیر گویند و تابعی که از انتگرال گیری از یک تابع حاصل می شود تابع اولیه گویند . اگر انتگرال گیری از تابع در یک محدوده خاص باشند به آن انتگرال معین گویند که نتیجه آن یک عدد است ولی اگر محدوده آن مشخص نباشد به آن انتگرال نامعین گویند.

محاسبه انتگرال

اکثر روش های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:

1.f تابعی در بازه (a,b) در نظر می گیریم .
2.پاد مشتق f را پیدا می کنیم که تابعی است مانند f که و داریم:
3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم:

بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم .
معمولاً پیدا کردن پاد مشتق تابع f کار ساده ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتند از :

انتگرال گیری بوسیله تغییر متغیر
انتگرال گیری جزء به جزء
انتگرال گیری با تغییر متغیر مثلثاتی
انتگرال گیری بوسیله تجزیه کسرها

روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می رود همچنین می توان بعضی از انتگرال ها با ترفند هایی حل کرد برای مثال می توانید به انتگرال گاوسی مراجعه کنید .

تقریب انتگرالهای معین

محاسبه سطح زیر نمودار بوسیله مستطیل هایی زیر نمودار.
هر چه قدرعرض مستطیل ها کوچک میشوندمقدار دقیق تری
از مقدار انتگرال بدست میآید.

انتگرال هایی معین ممکن است با استفاده از روش های انتگرال گیری عددی ،تخمین زده شوند.یکی از عمومی ترین روش ها ،روش مستطیلی نامیده می شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است.
از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه ای است. اگر چه روش های عددی مقدار دقیق انتگرال را به ما نمی دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می کند .

تعریف های انتگرال

از مهم ترین تعاریف در انتگرال می توان از انتگرال ریمان و انتگرال لبسکی(lebesgue) است. انتگرال ریمان بوسیله برنهارد ریمان در سال 1854 ارئه شد که تعریف دقیقی را از انتگرال ارائه می داد تعریف دیگر را هنری لبسکی ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می کرد.
از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال riemann-stieltjes اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند:

انتگرال ریمان
انتگرال لبسکی
انتگرال riemann-stieltjes
انتگرالهای چند گانه
روشهای انتگرال گیری

انتگرال نامعین

اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه:

نکته

اگر

جوابی برای

باشد ، فرمول

همه جوابها را به دست می‌دهد.

انتگرال نامعین

مجموعه همه پاد مشتق‌های یک تابع چون

را انتگرال نامعین

نسبت به

می‌نامند و با

نشان می‌دهند.
هرگاه فرمول

همه پادمشتق‌های

را به دست دهد، آنرا چنین مشخص می‌کنیم :

تابع

را انتگرال ده انتگرال و

را ثابت انتگرال‌گیری می‌نامیم. همچنین

نشان می‌دهد که متغیر انتگرال‌گیری

است.

خواص انتگرال

انتگرال مشتق یک تابع مشتق‌پذیر 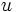برابر است با 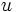به علاوه یک ثابت دلخواه.
یک ثابت را می‌توان از زیر نماد انتگرال‌گیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرال‌گیری اند ، نمی‌توان از زیر نماد انتگرال‌گیری بیرون آورد.)
انتگرال مجموع دو تابع برابر مجموع انتگرال‌های آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد.

فرمول های انتگرال گیری

در این دستور‌ها 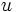یا متغیر مستقل است و یا تابعی مشتق‌پذیر از متغیر مستقل دیگری است.
اگر آنگاه

انتخاب مقدار ثابت انتگرال‌گیری

در حل یک معادله دیفرانسیل مانند

معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی

را تعیین می‌کنیم که همه جوابهای ممکن را به دست می‌دهد . سپس مقداری از

را تعیین می‌کنیم که جواب خاص مطلوب را به دست دهد.
اگر نقطه‌ای چون

از دامنه

را در نظر بگیریم و مقدار دلخواه

را برگزینیم ، می‌توان با قرار دادن

در معادله

و حل آن نسبت به

جوابی را یافت که از نقطه

بگذرد.به این ترتیب داریم

یا

.
خم

خمی است که از

می‌گذرد.

انتگرال‌گیری به کمک تغییر متغیر

در حل انتگرال‌ها با روش تغییر متغیر ، به جای

تابع پیوسته و مشتق پذیر

را قرار می دهیم، یعنی :

بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار می‌دهیم . یعنی:
از فرمول فوق به صورت زیر هم می‌توان استفاده کرد:

انتگرال‌گیری به روش جزء به جزء

دستور

موسوم به انتگرال‌گیری به روش جزء به جزء است که در آن

توابعی مشتق‌پذیر از

هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا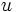

را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب می‌کنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را

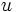فرض می‌کنند.

انتگرال گیری یکی از دو عامل اساسی در حسابان میباشد و از آنجائیکه برخلاف مشتق گیری، غیر-جزیی می باشد، جداول انتگرالهای شناخته شده اغلب مفید می باشند. این صفحه عمل معکوس مشتق گیری های معمول را فهرست نموده است؛ یک فهرست کاملتر را میتوانید در فهرست انتگرالها)) بیابید.

ما از C برای یک مقدار ثابت دلخواه در انتگرال گیری استفاده مینماییم، که در صورتی قابل تعیین خواهد بود که اطلاعی از مقدار انتگرال در نقطه‌ای داشته باشیم. لذا هر تابع تعداد نامحدودی انتگرال دارد.

:
:

:
:

:
:
:

:
:
:
:
:
:

:
:
:
:

:
:
:
:
:
:

این معادلات صرفا در شکل دیگری در جدول مشتقات بیان شده‌اند.

انتگرالهای معین

توابعی وجود دارند که عمل معکوس مشتق گیری را برای آن توابع نمی توان در شکل بسته نمایش داد. بهرحال، مقادیر انتگرالهای محدود این گونه توابع را میتوان در فاصله های متعارف محاسبه نمود. ذیلا، تعداد کمی از انتگرالهای محدود ارائه شده‌اند.

:
:
:
:
: