حساب تغییرات بدون در نظر گرفتن شرایط فرعی (معادله اویلر)
یکی از شاخه های وسیع ریاضیات، نوع خاصی از تعمیم حساب در آن است. حساب تغییرات (وردشها) در جستجوی یافتن مجموعه ای از مسیرها، خم ها، خمینه ها و ... است که به عنوان توابعی پیوسته و مشتق پذیر دارای اکسترم طولی هستند (که اغلب در مسائل فیزیکی از آن به عنوان کمینه یا بیشینه نیز یاد می شود). در ریاضیات، مقدار این اکسترمم بوسیله ی انتگرال معین زیر نمایش داده می شود:
که در آن
در مسئله ی کوتاه ترین خم زمانی (brachystochrone problem) که توسط یوهان برنولی (Johann BERNOULLI) به سال ۱۶۹۶ علناْ مطرح شد یافتن y ای در انتگرال فوق مطرح است که در آن بتوانیم تعریف ذیل را نمایان سازیم:
اگر دو نقطه ی p1 و p2 در ارتفاعات متفاوت اما نه واقع بر بالای یکدیگر، مفروض باشند، می خواهیم از جمیع خم های ممکن واصل آنها، خمی را بیابیم که یک نقطه ی مادی (material point) از p1 به p2 در امتداد آن و تحت تاثیر گرانی یا ثقل (صرفنظر از اصطکاک) در کوتاهترین زمان ممکن بلغزد.
مسئله ی فوق در آن زمان، ذهن ریاضیدانان پیشرو تمام اروپا، از قبیل: نیوتون، لایب نیتز، یاکوب برنولی، لوپیتال، هود (HUDDE)، فاتیو (FATIO) و ... را به خود مشغول کرد. از این زمان به بعد حساب تغییرات به عنوان عنوان دستگاه ریاضی خاصی توسعه یافته است.
مسئله ی بالا منجر به پیدایش تابع (y(x ای شد که بازای آن مقدار اکسترمم را برای تابع f مطرح کردیم. اما تابع لازم در این مسئله نوع خاصی از جوابی بود که باید در یک معادله ی دیفرانسیل کلی ترصادق باشد. اویلر به همراه لاگرانژ در تحویل مسئله ی تغییرات به معادلات دیفرانسیل توفیق یافت. معادله ی اویلر ـ لاگرانژ (Euler-Lagrange differential equation) یکی از فرمول های بنیادی حساب تغییرات یا وردش هاست.
وقتی  در انتگرال اول مقدار ثابتی داشته باشد، در این صورت می گوییم معادله ی اویلر ـ لاگرانژ
در انتگرال اول مقدار ثابتی داشته باشد، در این صورت می گوییم معادله ی اویلر ـ لاگرانژ
برقرار است. اگر مشتق نسبت به مولفه ی زمانی تابع y یعنی  را با مشتق مکانی
را با مشتق مکانی  تعویض کنیم، معادله به شکل زیر تبدیل خواهد شد:
تعویض کنیم، معادله به شکل زیر تبدیل خواهد شد:
در بسیاری از مسائل فیزیکی،  (مشتق جزئی
(مشتق جزئی  نسبت به
نسبت به  ) معلوم می شود که برابر صفر است، بنابراین در موارد خاصی از این قبیل معادله ی اویلر به معادله ی ساده شده و دارای شکل انتگرالی می انجامد که به اتحاد بلترامی (Beltrami identity) موسوم است:
) معلوم می شود که برابر صفر است، بنابراین در موارد خاصی از این قبیل معادله ی اویلر به معادله ی ساده شده و دارای شکل انتگرالی می انجامد که به اتحاد بلترامی (Beltrami identity) موسوم است:
برای سه متغیر مستقل (Arfken 1985, pp. 924-944) رابطه ی اویلر به شکل زیر تعمیم می یابد:
مسائلی که در حساب تغییرات مطرح می شود، اغلب با معادله ی اویلر به سادگی قابل حل هستند. برای اثبات این معادله، ابتدا مشتق انتگرال اکسترمم را با شرایط زیر و نسبت به q در نظر می گیریم:


که  . نماد دلتا به پیشنهاد لاگرانژ به عنوان وردش نوع اول مطرح شدکه مشتق نسبت به اکسترمال یا تابع y (در اینجا q) را نشان می دهد.
. نماد دلتا به پیشنهاد لاگرانژ به عنوان وردش نوع اول مطرح شدکه مشتق نسبت به اکسترمال یا تابع y (در اینجا q) را نشان می دهد.
با انتگرال گیری جزء به جزء از جمله ی دوم و استفاده از







داریم:
با ترکیب انتگرال اول و انتگرال سوم از معادله ی فوق داریم:
اما ما تنها مسیر را تغییر می دهیم، یعنی نقاط ابتدا و انتها ثابت می مانند. لذا  . درنتیجه معادله ی اخیر به شکل زیر تقلیل خواهد یافت:
. درنتیجه معادله ی اخیر به شکل زیر تقلیل خواهد یافت:
در این رابطه ما به دنبال مقادیر ثابت نظیر  هستیم. اگر شرط اکسترمال را در نظر بگیریم باید به دنبال نقاطی نظیر مینیمم، ماکزیمم و عطف بگردیم که این نقاط برای تغیر کوچک
هستیم. اگر شرط اکسترمال را در نظر بگیریم باید به دنبال نقاطی نظیر مینیمم، ماکزیمم و عطف بگردیم که این نقاط برای تغیر کوچک  بایستی صفر شوند. پس
بایستی صفر شوند. پس
که این همان معادله ی اویلر ـ لاگرانژ است.
همچنین وردش در  می تواند برحسب پارامتر
می تواند برحسب پارامتر  به صورت زیر نوشته شود:
به صورت زیر نوشته شود:
![int[f(x,y+kappav,y^.+kappav^.)-f(x,y,y^.)]dt](http://www.bargozideha.com/static/portal/20/201785-209452.gif)


که






مشتقات دوم و سوم و ... به همین صورت خواهند بود و وردش ها نیز عبارت اند از




وردش دوم را می توان با اعمال تغییر
به صورت زیر مجددا توصیف کرد:
اما
حال  را به شکلی انتخاب می کنیم که
را به شکلی انتخاب می کنیم که
و تصدیق معادله ی
نهایتا خواهیم داشت:

برای دسترسی به کتاب هایی در زمینه ی حساب تغییرات به بخش کتاب خانه وبلاگ مراجعه کنید.
Dated 2008/06/29
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Forsyth, A. R. Calculus of Variations. New York: Dover, pp. 17-20 and 29, 1960.
Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, p. 44, 1980.
Lanczos, C. The Variational Principles of Mechanics, 4th ed. New York: Dover, pp. 53 and 61, 1986.
Morse, P. M. and Feshbach, H. "The Variational Integral and the Euler Equations." §3.1 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 276-280, 1953.
مطالب مشابه :
اندازه گیری سرعت و دبی
با استفاده از رابطه ی برنولی و دانستن چگالی پروب رابطه ی 2 به اثبات رسیده است که
آیرودینامیک
حرکت آونگ بتدریج کند میشود و کوشید رابطه ی قضیه ی برنولی را اثبات کند و
آیرودینامیک
او متوجه شد که حرکت آونگ بتدریج کند می شود و کوشید رابطه ی ی برنولی را اثبات کند
گزارش کار آز-مکانیک سیالات
هدف در این آزمایش تعیین رابطه ای تجربی 1-اثبات سرعت 2gh v در نوشتن معادله برنولی از در
لوله پیتوت چیست ؟ pitot tube
به این علت در رابطه ی برنولی ضریب تصحیحی زیرا در عمل به اثبات رسیده است که برای اندازه
آمار و احتمالات مهندسی
رابطهی توزیع فاصلهی اطمینان برای نسبت p با تعداد نمونههای زیاد در توزیع برنولی فاصله
حساب تغییرات بدون در نظر گرفتن شرایط فرعی (معادله اویلر)
که توسط یوهان برنولی رابطه ی اویلر به شکل برای اثبات این معادله، ابتدا مشتق
برچسب :
اثبات رابطه ی برنولی

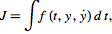









![int[(partialL)/(partialq)deltaq+(partialL)/(partialq^.)(d(deltaq))/(dt)]dt,](http://www.bargozideha.com/static/portal/25/253572-845993.gif)

![int(partialL)/(partialq^.)(d(deltaq))/(dt)dt=int(partialL)/(partialq^.)d(deltaq)=[(partialL)/(partialq^.)deltaq]_(t_1)^(t_2)-int_(t_1)^(t_2)(d/(dt)(partialL)/(partialq^.)dt)deltaq.](http://www.bargozideha.com/static/portal/10/107458-582564.gif)
![deltaJ=[(partialL)/(partialq^.)deltaq]_(t_1)^(t_2)+int_(t_1)^(t_2)((partialL)/(partialq)-d/(dt)(partialL)/(partialq^.))deltaqdt.](http://www.bargozideha.com/static/portal/80/803159-957950.gif)













![I_2+[v^2lambda]_2^1=int_1^2[v^2(f_(yy)+lambda^.)+2vv^.(f_(yy^.)+lambda)+v^.^2f_(y^.y^.)]dt.](http://www.bargozideha.com/static/portal/81/812453-504450.gif)
![[v^2lambda]_2^1=0.](http://www.bargozideha.com/static/portal/72/724511-222087.gif)







