تحلیل رگرسیون و رگرسیون کاذب
تحلیل رگرسیون
تحلیل رگرسیونی یا تحلیل وایازشی فن و تکنیکی آماری برای بررسی و مدلسازی ارتباط بین متغیرها است. رگرسیون تقریباً در هر زمینهای از جمله مهندسی، فیزیک، اقتصاد، مدیریت، علوم زیستی، بیولوژی و علوم اجتماعی برای برآورد و پیشبینی مورد نیاز است.
تحلیل رگرسیونی، یکی از پرکاربردترین روش در بین تکنیکهای آماری است.
تعریف لغوی
واژه رگرسیون(Regression) را از لحاظ لغوی در فرهنگ لغت به معنی پسروی، برگشت و بازگشت است. اما از دید آمار و ریاضیات به مفهوم بازگشت به یک مقدار متوسط یا میانگین بهکارمیرود. بدین معنی که برخی پدیدهها به مرور زمان از نظر کمی به طرف یک مقدار متوسط میل میکنند.
تاریخچه
در سال ۱۸۷۷ فرانسیس گالتون (به انگلیسی: Francis Galton) در مقالهای که درباره بازگشت به میانگین منتشر کردهبود. اظهار داشت که متوسط قد پسران دارای پدران قدبلند، کمتر از قد پدرانشان میباشد. به نحو مشابه متوسط قد پسران دارای پدران کوتاهقد نیز، بیشتر از قد پدرانشان گزارش شدهاست. به این ترتیب گالتون پدیده بازگشت به طرف میانگین را در دادههایش مورد تأکید قرارداد. برای گالتون رگرسیون مفهومی زیستشناختی داشت، اما کارهای او توسط کارل پیرسون (به انگلیسی: Karl Pearson) برای مفاهیم آماری توسعه دادهشد. گرچه گالتون برای تأکید بر پدیده «بازگشت به سمت مقدار متوسط» از تحلیل رگرسیون استفاده کرد، اما به هر حال امروزه واژه تحلیل رگرسیون جهت اشاره به مطالعات مربوط به روابط بین متغیرها به کار بردهمیشود.
رگرسیون کاذب
رگرسیون کاذب (به انگلیسی: regression) با فرض اینکه متغیرهای 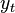 و
و  مانا میباشند تخمینهای ما از پارامترها و تستهای
مانا میباشند تخمینهای ما از پارامترها و تستهای  و
و  درست میباشد. برای نشاندادن سازگاری تخمینهای حداقل مربعات معمولی، ما از این نتایج زمانی که اندازه نمونه افزایش مییابد و واریانس نمونه به واریانس جامعه همگرا میشود، استفاده میکنیم. متأسفانه وقتی سری نامانا باشد واریانس خوش تعریف نیست، زیرا حول یک میانگین ثابت نوسان نمیکند. برای توضیح بیشتر دو متغیر
درست میباشد. برای نشاندادن سازگاری تخمینهای حداقل مربعات معمولی، ما از این نتایج زمانی که اندازه نمونه افزایش مییابد و واریانس نمونه به واریانس جامعه همگرا میشود، استفاده میکنیم. متأسفانه وقتی سری نامانا باشد واریانس خوش تعریف نیست، زیرا حول یک میانگین ثابت نوسان نمیکند. برای توضیح بیشتر دو متغیر 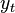 و
و  را در نظر بگیرید که بوسیله یک فرآیند گام تصادفی تعریف میشود.
را در نظر بگیرید که بوسیله یک فرآیند گام تصادفی تعریف میشود.
که  و
و  دارای توزیع مستقل میباشد.هیچ دلیلی برای ارتباط بین
دارای توزیع مستقل میباشد.هیچ دلیلی برای ارتباط بین 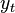 و
و  وجود ندارد. یک محقق اگراثر
وجود ندارد. یک محقق اگراثر 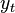 را روی
را روی  و یک جزء ثابت رگرس کند و رگرسیون زیر را انجام دهد :
و یک جزء ثابت رگرس کند و رگرسیون زیر را انجام دهد :

نتایج این رگرسیون ممکن است بوسیله r^۲ بالا و خود همبستگی بالا بین باقیماندهها و همچنین دارای ارزش معنیداری برای پارامتر  باشد. این پدیده به رگرسیون کاذب معروف است. در این گونه از موارد دو سری نامانا ارتباط کاذبی دارند به این علت که که هر دوی آنها در طول زمان تغییر میکنند و تابعی از زمانند. همانطور که گراجر و نی یو بلد بیان کردند در این حالت رگرسیون دارای r^۲ بالا؛ و آماره دوربین واتسون پایین خواهدبود و تستهای
باشد. این پدیده به رگرسیون کاذب معروف است. در این گونه از موارد دو سری نامانا ارتباط کاذبی دارند به این علت که که هر دوی آنها در طول زمان تغییر میکنند و تابعی از زمانند. همانطور که گراجر و نی یو بلد بیان کردند در این حالت رگرسیون دارای r^۲ بالا؛ و آماره دوربین واتسون پایین خواهدبود و تستهای  و
و  ممکن است خیلی گمراهکننده باشند. دلیل آن نیز این است که توزیعهای آمارههای تستهای سنتی خیلی متفاوت از نتایجی که تحت فرض مانایی گرفتهمیشود، میباشد. بخصوص همانطور که فلیپس (۱۹۸۷)نشان داد؛ همانطور که اندازه نمونه افزایش مییابد نمیتوان به معنیداری تخمین زن حداقل مربعات معمولی و آمارههای تستهای
ممکن است خیلی گمراهکننده باشند. دلیل آن نیز این است که توزیعهای آمارههای تستهای سنتی خیلی متفاوت از نتایجی که تحت فرض مانایی گرفتهمیشود، میباشد. بخصوص همانطور که فلیپس (۱۹۸۷)نشان داد؛ همانطور که اندازه نمونه افزایش مییابد نمیتوان به معنیداری تخمین زن حداقل مربعات معمولی و آمارههای تستهای  و
و  و آماره دوربین واتسون اعتماد کرد. دلیل آن این است که
و آماره دوربین واتسون اعتماد کرد. دلیل آن این است که 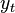 و
و  متغیرهای
متغیرهای  میباشد و جزء خطا نیز یک متغیر نامانا
میباشد و جزء خطا نیز یک متغیر نامانا میباشد.
میباشد.
اگر ارزشهای گذشته هر دو متغیر وابسته و مستقل را در رگرسیون وارد کنیم مشکل رگرسیون کاذب حل میشود. در این حالت تخمینهای حداقل مربعات معمولی برای همه پارامترها سازگار میباشد.
شیوهها
شیوههای مهم تحلیلهای رگرسیونی به شرج زیر هستند.
- رگرسیون خطی ساده
- رگرسیون خطی چندگانه
- رگرسیون فازی
- رگرسیون لجستیک
این تنوع باعث شدهاست که بتوان به راحتی هر نوع دادهای (اغلب از نوع دادههای پیوسته) را تحلیل کرد و به راحتی نتیجهگیری نمود.
محاسبه
برای انجام یک تحلیل رگرسیونی ابتدا تحلیلگر حدس میزند که بین دو متغیر، نوعی ارتباط وجود دارد، در حقیقت حدس میزند که یک رابطه به شکل یک خط بین دو متغیر وجود دارد و سپس به جمعآوری اطلاعات کمی از دو متغیر میپردازد و این دادهها را به صورت نقاطی در یک نمودار دو بعدی رسم میکند.
نرم افزارها
نرم افزارهای بسیاری هستند که قابلیت محاسبه رگرسیون را دارند و مشهورترین آنها عبارتند از:
- نرم افزار اکسل (که ساده ترین نرم افزار است)
- اسپیاساس SPSS
- اسپلاس +S یا Plus-S
- سس (نرمافزار) SAS
- نرم افزار R
رگرسیون کاذب چیست؟
سری های زمانی، یکی از مهم ترین داده های آماری مورد استفاده در تجزیه و تحلیل تجربی هستند. در تحقیقات همواره چنین فرض می کنیم که سری زمانی مانا است و اگر این حالت وجود نداشته باشد، آزمون های آماری متعارفی که اساس آن ها بر پایه t، F، خی دو و آزمون های مشابه بنا شده، مورد تردید قرار می گیرد. در رگرسیون هایی که داده های آن از نوع سری زمانی است، اگر متغیرهای سری زمانی مانا نباشند، ممکن است مشکلی به نام رگرسیون کاذب یا رگرسیون ساختگی به وجود آید. در این گونه رگرسیون ها، در عین حالی که هیچ رابطه ی با مفهومی بین متغیرها وجود ندارد ولی ضریب تعیین R2 بزرگ و مقدار آماره t ضرایب نیز بزرگ به دست می آید و این ممکن است باعث استنباط های غلط در مورد میزان ارتباط بین متغیرها شود. بنابراین لازم است همواره مواظب عواقب استفاده از داده های سری زمانی نامانا و امکان بروز رگرسیون کاذب باشیم.
از طرفی اگر در یک مدل، متغیرها نامانا شدند، به جای سطح، اولین تفاضل ( یا تفاضل مراتب بالاتر) آن ها می تواند مانا بوده و از ان ها در مدل استفاده کنیم و مدل را بر اساس متغیرهای جدید تخمین بزنیم؛ در این حالت مشکل رگرسیون کاذب بر طرف می شود. حال این سوال مطرح می شود که آیا مشکل دیگری وجود ندارد. هنگامی که از تفاضل ها در برآورد ضرایب یک الگو استفاده می کنیم، اطلاعات ارزشمندی را در رابطه با سطح متغیرها از دست می دهیم. هر چند شرط مانایی متغیرهای سری زمانی یک رابطه ی رگرسیونی را می توان از طریق تفاضل گیری تامین کرد ولی با تفاضل گیری مرتبه اول ( یا مراتب بالاتر)رابطه ی بلند مدت بین سری های زمانی را از دست می دهیم. ( این رابطه ی بلند مدت بین دو سری زمانی ناشی از سطوح دو متغیر است نه تفاضل مرتبه اول آنها). اینجاست که هم انباشتگی به کمک ما می آید تا بتوان رگرسیون را بدون هراس ازکاذب بودن بر اساس سطح متغیرهای سری زمانی برآورد کرد.
مطالب مشابه :
محاسبه رگرسیون خطی-آمار توصیفی بدون نیاز به نرم افزار
آمار - محاسبه رگرسیون خطی-آمار توصیفی بدون نیاز به نرم افزار - همه چيز براي آماريها: کتاب، حل
آموزش نحوه محاسبه مدل رگرسیون لجستیک Binomial logistic regression در نرمافزار SPSS
آمار برای همه - آموزش نحوه محاسبه مدل رگرسیون لجستیک Binomial logistic regression در نرمافزار SPSS - آمار
محاسبه رگرسیون توبیت (Tobit Regression) در Stata
یادداشت های اقتصادی - محاسبه رگرسیون توبیت (Tobit Regression) در Stata - علی رئوفی/ دانشجوی دکترای
محاسبه رگرسیون خطی
بچه های زیست شناسی دانشگاه محقق اردبیل - محاسبه رگرسیون خطی - گزارش کار و مقاله - بچه های زیست
کاربرد آنالیز رگرسیون خطی(Linear Regression) با استفاده از نرم افزار SAS
با توجه به سوالات مکرر دانشجویان در مورد نحوه محاسبه رگرسیون خطی در نرم افزار sasبر آن شدم تا
آموزش مقدماتی رگرسیون با نرم افزار اکسل
آمار؛کلید توسعه - آموزش مقدماتی رگرسیون با نرم افزار اکسل - برنامه ریزی بدون آمار ، تیری است
تحلیل رگرسیون و رگرسیون کاذب
» معرفی گروه و خدمات آن: ( دوشنبه ۳ تیر۱۳۹۲ ) » ـ فرمول محاسبه حجم نمونه در مطالعات مشاهده ای
آموزش رگرسیون چند متغیره در spss
محــاسبه, آماره, آماره t در ادامه یک فایل آموزش تصویری رگرسیون چند متغیره در نرم افزار
رگرسیون در علوم دامی
math.statistic.genetic - رگرسیون در علوم دامی - ریاضی آمار کامپیوتر ژنتیک
برچسب :
محاسبه رگرسیون


