اندازه و انتگرال لبگ

اندازه ی لبگ (Lebesgue Measure)، توسیع مفاهیم طول و مساحت به مجموعه های بسیار پیچیده است. مجموعه ی باز 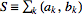S=sum_(k)(a_k,b_k)  شامل عناصر مجزا (disjoint) (یعنی اشتراک آنها تهی باشد. می توان از انها با عنوان مجموعه های مستقل نیز یاد کرد.)، معلوم است. اندازه ی لبگ به صورت زیر تعریف می شود

mu_L(S)=sum_(k)(b_k-a_k).                       

چنانچه مجموعه ی انتخابی بسته  (closed set) باشد یعنی S^'=[a,b]-sum_(k)(a_k,b_k)، آنگاه داریم

mu_L(S^')=(b-a)-sum_(k)(b_k-a_k).                        

یک پاره خط به طول واحد، اندازه ی لبگ ۱ دارد، اندازه ی لبگ مجموعه ی کانتور (Cantor set) صفر است. اندازه ی مینکوفسکی (Minkowski measure) یک مجموعه ی بسته کراندار ، در حقیقت همان مفهوم اندازه ی لبگ را در پی دارد (Ko 1995).

انتگرال لبگ (Lebesgue Integral) برحسب جملات کران بالا و پایین و بکارگیری اندازه ی لبگ یک مجموعه حاصل می شود. در این تعریف، از جمع لبگ (Lebesgue sum) S_n=sum_(i)eta_imu(E_i) که در آن eta_i مقدار تابع در زیربازه ی i و mu(E_i) اندازه ی لبگ مجموعه ی E_i ازنقاطی است که برای آنها مقادیر تقریباْ برابر با eta_i هستند. این انتگرال، دسته ی عظیمی از توابع انتگرالپذیر که انتگرال ریمان (Riemann integral) آنها را در بر نمی گیرد، را تحت پوشش قرار می دهد.

انتگرال لبگ یک تابع  f در فضای اندازه (measure space) X، به صورت زیر نوشته می شود

           int_Xf,                             

یا اغلب

           int_Xfdmu                             

که تاکیدی بر این موضوع باشد که انتگرال نسبت به اندازه (measure) mu گرفته می شود.          

منابع:

Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 4, 1991.

Kestelman, H. "Lebesgue Measure." Ch. 3 in Modern Theories of Integration, 2nd rev. ed. New York: Dover, pp. 67-91, 1960.

Ko, K.-I. "A Polynomial-Time Computable Curve whose Interior has a Nonrecursive Measure." Theoret. Comput. Sci. 145, 241-270, 1995.

Kestelman, H. "Lebesgue Integral of a Non-Negative Function" and "Lebesgue Integrals of Functions Which Are Sometimes Negative." Chs. 5-6 in Modern Theories of Integration, 2nd rev. ed. New York: Dover, pp. 113-160, 1960.

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 141, 1984.


مطالب مشابه :


انتگرال ریمان

دریای ریاضی - انتگرال ریمان - آموزش ریاضی، دانلود رایگان جزوه های دانشگاهی،کتاب های



انتگرال ریمان

انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته می‌شود.



انتگرال ریمان

ریاضیات دبیرستان - انتگرال ریمان - - ریاضیات دبیرستان این وبلاگ برای تمامی علاقمندان به



انتگرال

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است.



اندازه و انتگرال لبگ

انتگرال لبگ (Lebesgue این انتگرال، دسته ی عظیمی از توابع انتگرالپذیر که انتگرال ریمان (Riemann



انتگرال

انتگرال معین بنا به تعریف، نماد را انتگرال معین نامیده و حاصل آن را به ازای عددی به صورت زیر



انتگرال و دعوای نیوتن و لایب نیتز

گنجینه ریاضی - انتگرال و دعوای نیوتن و لایب نیتز - علمی، پژوهشی، فرهنگی و انتشاراتی



برنهارد ریمان

دانلود کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry



انالیز ریاضی

در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه



برنهارد ریمان

دانلود رایگان کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry - دانلود رایگان کتب و



برچسب :