اعداد رمزی

اعداد 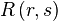$R \left ( r,s \right )$ در قضیهٔ رمزی ( و بسط یافتهٔ آن‌ها در موارد با بیش از دو رنگ) تحت عنوان اعداد رمزی شناخته می‌شوند. یک حد بالا برای 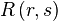$R\left ( r,s \right )$ را، می‌توان از اثبات قضیه استخراج کرد و سایر استدلال‌ها نیز حد پایین برای آن ارائه می‌کنند.(نخستین حد پایین توسط Paul Erdős با استفاده از روش احتمالاتی به دست آمد.) هر چند شکاف بزرگی میان مقادیر حد پایین و حد بالا وجود دارد. من تبع آن تعداد بسیار اندکی از r وs‌ها هستند که ما برای آن‌ها مقدار دقیق 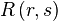$R \left ( r,s \right )$ را می‌دانیم.محاسبهٔ حد پایین L برای 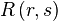$R \left ( r,s \right )$ معمولاً نیازمند ارائهٔ یک رنگ آمیزی گراف 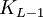$K_{L-1}$ با دو رنگ قرمز و آبی است به طوری که هیچ زیرگراف آبی 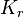و هیچ زیرگراف قرمز 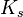در آن یافت نشود. هر چند که بررسی حالت‌های مختلف رنگ آمیزی گراف 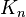با افزایش مقدار n از نظر محاسباتی بسیار پیچیده خواهد شد. تعداد حالت‌های رنگ آمیزی رشدی بالاتر از رشد نمایی(exponentially) دارد.

در حال حاضر حتی مقدار دقیق 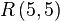$R \left( 5,5 \right )$ شناخته شده‌است هر چند که از قبل می‌دانستیم که مقدار آن بین 43(توسط Geoffrey Exoo) و 49 (Brendan McKay، وStanisław Radziszowski) قرار دارد. احتمال داده می‌شود که مقدار دقیق 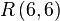$R \left ( 6,6 \right )$ برای همیشه مجهول بماند. Paul Erdős می‌گوید:

" بیگانگانی( نیروهای خارجی) را تصور کنید که بسیار نیرومندتر از ما بر روی زمین هستند و از ما خواسته‌اند که مقدار 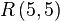$R \left ( 5,5 \right )$ را محاسبه کنیم و در غیر این صورت سیارهٔ ما را نابود خواهند کرد. در این حالت ما باید تمام کامپیوترها و ریاضی دان هایمان را به کار بگیریم و برای یافتن مقدار مورد نظر به شدت تلاش کنیم. حال به جای این تصور کنید که از ما خواسته شده تا مقدار 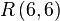$R \left ( 6,6 \right )$ را محاسبه نماییم، در این وضعیت ما باید تمام تلاشمان را برای نابود کردن بیگانگان به کار ببریم!"

مقدار 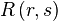$R \left ( r,s \right )$ برای مقادیر r و s تا 10 در جدول زیر نشان داده شده‌است. از آن جایی که در بسیاری از موارد مقدار دقیق را نمی‌دانیم، بهترین حدود یافت شده در جدول به نماش گذاشته شده‌است. 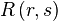$R \left ( r,s \right )$ برای مقادیر r و s کوچک تر از 3 به صورت R(1,s) = 1و R(2,s) = s برای تمام مقادیرs داده شده‌است.

r,s	1	2	3	4	5	6	7	8	9	10
1	1	1	1	1	1	1	1	1	1	1
2	1	2	3	4	5	6	7	8	9	10
3	1	3	6	9	14	18	23	28	36	40–43
4	1	4	9	18	25	36–41	49–61	56–84	73–115	92–149
5	1	5	14	25	43–49	58–87	80–143	101–216	125–316	144–442
6	1	6	18	36–41	58–87	102–165	113–298	132–495	169–780	179–1171
7	1	7	23	49–61	80–143	113–298	205–540	217–1031	241–1713	289–2826
8	1	8	28	56–84	101–216	132–495	217–1031	282–1870	317–3583	6090-331
9	1	9	36	73–115	125–316	169–780	241–1713	317–3583	565–6588	581–12677
10	1	10	40–43	92–149	144–442	179–1171	289–2826	6090-331	581–12677	798–23556

در جدول یک تقارن ناچیز در میان قطر نیز وجود دارد. جدول فوق از جدول بزرگ تری که توسط Stanisław Radziszowski تالیف شده، اقتباس شده‌است. در سال ۲۰۱۲ قضیه 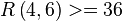$R \left ( 4,6 \right ) >= 36$ توسط Geoffrey Exoo اثبات شد.

یک مثال از چندین رنگ : R(3,3,3) = 17

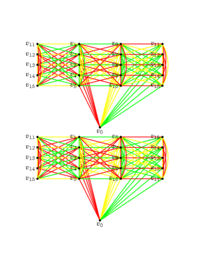
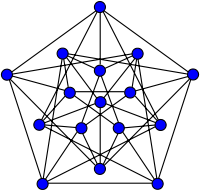
گراف Clebsch

یک عدد رمزی رنگارنگ یک عدد رمزی است که در آن برای رنگ آمیزی از 3 رنگ یا بیشتر استفاده می‌شود. فقط یک عدد رمزی رنگارنگ وجود دارد که مقدار دقیق آن شناخته شده‌است و آن R(3,3,3) = 17 است.

یالی از یک گراف کامل را درنظر بگیرید که با 3 رنگ قرمز، آبی و زرد رنگ آمیزی شده‌است. علاوه بر این فرض کنید که یال مورد نظر هیچ مثلث هم رنگی را تشکیل نمی‌دهد. یک راس دلخواه v را انتخاب کنید. مجموعهٔ رئوسی که یک یال سبز به v داده‌اند را در نظر بگیرید. این مجموعه همسایگی سبز راس v نامیده می‌شود. همسایگی سبز v نمی‌تواند شامل هیچ یال سبزی باشد، زیرا در غیر این صورت مثلث سبزی وجود خواهد داشت که متشکل از دو نقطهٔ انتهایی آن یال سبز و راس v خواهد بود. پس یال‌های رنگ آمیزی شده در همسایگی سبز v تنها با دو رنگ قرمز و زرد رنگ آمیزی شده‌اند. از آن جایی که R(3,3) = 6 است همسایگی سبز v می‌تواند حداکثر شامل 5 راس باشد. به طور مشابه همسایگی‌های قرمز و زرد v نیز هر کدام حداکثر می‌توانند 5 راس داشته باشند. از آن جایی که هر راس به جز خود v در یکی از همسایگی‌های سبز، قرمز یا زرد v قرار گرفته، گراف کامل حداکثر می‌تواند 1 + 5 + 5 + 5 = 16 راس داشته باشد. در نتیجه داریم : R(3,3,3) ≤ 17

برای این که ببینیم R(3,3,3) ≤ 17 کافی است یال‌های یک گراف کامل با 16 راس را با سه رنگ متفاوت رنگ آمیزی کنیم و در عین حال از ایجاد مثلث‌های تک رنگ بپرهیزیم . به این نتیجه خواهیم رسید که دقیقا دو روش برای رنگ آمیزی K16 با این شرایط وجود دارد که آن‌ها را رنگ آمیزی تابیده(معوج) و ناتابیده می‌نامیم. هر دو روش رنگ آمیزی در شکل سمت چپ در بالا نشان داده شده‌است.شکل بالایی رنگ آمیزی ناتابیده و شکل پایینی رنگ آمیزی تابیده را نشان می‌دهد.

پس R(3,3,3)=17.

اگر شما هر رنگی از رنگ‌های تابیده یا ناتابیدهٔ گراف 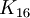$K_{16}$ را انتخاب کنید و گرافی را در نظر بگیرید که یال‌هایش دقیقا یال‌هایی با همان رنگ ویژه باشد آن گاه به گراف Clebsch دست خواهیم یافت .

دقیقا دو روش برای رنگ آمیزی یال‌های گراف 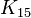$K_{15}$ با سه رنگ وجود دارد به گونه‌ای که از ایجاد مثلث‌های تک رنگ پرهیز کنیم . این گراف را می‌توان با حذف کردن هر راس دلخواه از گراف تابیده یا ناتابیدهٔ K16 که به طور مطلوب رنگ آمیزی شده، به دست آورد.

علاوه بر این دقیقا 115 یال برای رنگ آمیزی 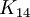$K_{14}$ با سه رنگ وجود دارد به گونه‌ای که در آن از ایجاد مثلث‌های تک رنگ جلوگیری شود.

اعداد رمزی

یک مثال از چندین رنگ : R(3,3,3) = 17

مطالب مشابه :

اعداد رمزی

فعالیت تکمیلی برای شناخت اعداد و رنگ ها

قضیه رمزی(ramsey)

آموزش جمع اعداد با حاصل دو رقمی

فعالیت تکمیلی برای شناخت اعداد و رنگ ها

آموزش ساخت برنامه رنگ آمیزی نقاشی با آدوب فلش ( یه شروع کلیدی )

رنگ‌آمیزی گراف

جمع اعداد یک رقمی با حاصل دو رقم در پایه ی اول