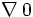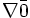حل معادله ی درجه ی 3

تاریخچه

معادلات درجه سوم برای اولین بار توسط ریاضیدانان هندسی در حدود 400 سال قبل از میلاد مورد توجه قرار گرفت. در بین ریاضیدانان پارسی، عمر خیام (1123-1048) راه حلی را برای حل معادله درجه سوم ابداع کرد. او در این روش با استفاده از هندسه نشان داد که چگونه با استفاده از روش هندسی می‌توان به جواب عددی معادله رسید با استفاده از جدول مثلثاتی. همچنین در حول و حوش قرن 16، یک ریاضیدان ایتالیایی به نام scipione، روشی را برای حل کلاسی از معادلات درجه سوم که به صورت 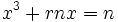می‌باشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را می‌توان به صورت گفته شده کاهش داد.

ریشه‌های معادله

هر معادله درجه سوم حقیقی حداقل یک جواب حقیقی دارد. این استدلال نتیجه مستقیم قضیه مقدار میانگین است.
برای معادله درجه سوم یک معادله مشخصه‌ای به صورت زیر بیان می‌شود که امکان وجود ریشه‌ها را بیان می‌کند. بنابراین با فرض

موارد زیر نتجه می‌شود:

: آنگاه معادله حتما 3 ریشه مجزا خواهد داشت.
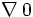: آنگاه معادله حتما یک ریشه حقیقی و. یک جفت ریشه مختلط خواهد داشت.
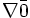: آنگاه معادله حداقل دو ریشه دارد.

برای تصمیم گیری در مورد اینکه معادله چند ریشه متمایز دارد را به صورت زیر تشکیل می‌دهیم:

حال دو حالت در نظر می‌گیریم:
اگر ، آنگاه هر 3 ریشه تکراری است.
در غیر اینصورت معادله 2 ریشه تکراری و یک ریشه مجزا خواهد داشت.

روش کاردانو برای پیدا کردن ریشه‌های معادله درجه سوم

در ابتدا معادله داده شده را به فرم کلاسیک تبدیل می‌کنیم، همین معادله داده شده را به ضریب تقسیم می‌کنیم.
حال با تغییر متغیر: معادله را به فرم زیر تبدیل می‌کنیم.

بطوری که و معادله به دست آمده را معادله تقلیل یافته می‌نامیم.
حال فرض می‌کنیم که بتوانیم اعداد u و v را طوری پیدا کنیم که:

حل جواب معادله داده شده با فرض t=v-u به دست می‌آید این مطلب بطور مستقیم با تعقیب متغیر t در (2) قابل بررسی می‌باشد. به عنوان یک نتیجه از اتحاد معادله درجه سوم معادله

(3) قابل حل است. با حل معادله درجه دوم برای v که به دست می‌آید

با قرار دادن این مقادیر در 3 خواهیم داشت

که از حل این معادله که یک معادله درجه 2 از می‌باشد خواهیم داشت
حال چون و پس