لگاریتم (1)
پرش به: ناوبری,
جستجو
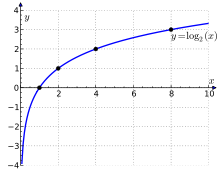
 نمودار لگاریتم در پایهٔ ۲ که محور xها (محور افقی) را در نقطهٔ ۱ قطع
میکند، بالا میرود و به ترتیب از نقطههای (۲،۱) و (۴،۲) و (۸،۳) عبور
میکند. به ازای اعداد نزدیک صفر، منحنی لگاریتم به محور عمودی y بسیار
نزدیک میشود ولی هرگز با آن مماس نمیشود یا آن را قطع نمیکند.
نمودار لگاریتم در پایهٔ ۲ که محور xها (محور افقی) را در نقطهٔ ۱ قطع
میکند، بالا میرود و به ترتیب از نقطههای (۲،۱) و (۴،۲) و (۸،۳) عبور
میکند. به ازای اعداد نزدیک صفر، منحنی لگاریتم به محور عمودی y بسیار
نزدیک میشود ولی هرگز با آن مماس نمیشود یا آن را قطع نمیکند.
لُگاریتم یک عدد در یک پایه، برابر با توانی
از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰،
برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت  نمایش میدهیم. مانند:
نمایش میدهیم. مانند: 
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسان تر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و خطکشهای لغزنده ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند:

مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شده است؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض بویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. لگاریتم دو دویی نیز در مبنای ۲ نوشته میشود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسیبل یکایی لگاریتمی است که برای نشان دادن فشار صدا و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دان میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کرد.
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود.
انگیزهٔ اولیه و تعریف
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
به توان رساندن
توان سوم عددی مانند b برابر است با 3 بار ضرب b در خودش. حال اگر b به توان یک عدد طبیعی مانند n برسد به معنی n بار ضرب کردن b در خودش است که به صورت زیر نمایش میدهیم:

در صورتی که n عدد طبیعی نباشد، آنگاه bn جواب دیگری خواهد داشت. مانند 1- که b-1 برابر معکوس b است.
تعریف
لگاریتم عددی مانند y در پایهٔ b عبارت است از یافتن عددی که اگر b به توان آن عدد برسد برابر با y شود. به عبارت دیگر جواب x معادلهٔ زیر برابر با لگاریتم y در پایهٔ b خواهد بود.

پایهٔ b باید یک عدد حقیقی مثبت و نامساوی 1 باشد و y نیز باید یک عدد مثبت باشد.[۲]

چند نمونه
نمونهٔ یکمبرای نمونه ۴ = (۱۶) log۲ چون ۱۶ = ۲ × ۲ × ۲ × ۲ = ۲۴
نمونهٔ دومبرای توانهای منفی نیز لگاریتم معتبر است مانند:

چون
 نمونهٔ سوم
نمونهٔ سوم(۱۵۰) log۱۰ تقریبا برابر است با ۲٫۱۷۶ عددی میان ۲ و ۳ چون ۱۵۰ خود عددی است میان ۱۰۰ = ۱۰۲ و ۱۰۰۰ = ۱۰۳ همچنین در هر پایهای  و
و  چون به ترتیب:
چون به ترتیب:  و
و  است.
است.
قوانین لگاریتم
نوشتار اصلی: فهرست اتحادهای لگاریتمیرابطههای مختلفی به عنوان قوانین لگاریتم وجود دارند که میتوانند میان فرمولهای لگاریتمی رابطه برقرار کنند.
ضرب، تقسیم، توان، ریشه
لگاریتم حاصل ضرب چند عدد برابر است با مجموع لگاریتمهای تک تک آن عددها. لگاریتم نسبت دو عدد (تقسیم) برابر است با تفاضل لگاریتم آن دو عدد. لگاریتم توان p ام یک عدد برابر است با p برابر لگاریتم آن عدد. لگاریتم ریشهٔ p ام یک عدد برابر است با لگاریتم آن عدد تقسیم بر p. جدول زیر قوانین لگاریتم را همراه با یک نمونه نشان دادهاست:
| رابطه | نمونه | |
|---|---|---|
| ضرب |  |
 |
| تقسیم |  |
 |
| توان |  |
 |
| ریشه | ![\log_b \sqrt[p]{x} = \frac {\log_b (x)} p \,](http://www.bargozideha.com/static/portal/18/182701-320312.png) |
 |
تغییر پایه
میتوان  را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:

بیشتر ماشین حسابهایی که در دسترس اند لگاریتم را تنها در مبنای ۱۰ و عدد نپر[۳] محاسبه میکنند و لگاریتم در پایههای دیگر را به کمک رابطهٔ بالا محاسبه میکنند:

همچنین اگر عددی مانند x و مقدار لگاریتم آن را در یک مبنای نامشخص b داشته باشیم  حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
حال میتوان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:

پایههای ویژه
پایههای ویژهٔ لگاریتم عبارتند از ۱۰، ۲ و عدد e (عدد گنگی تقریبا برابر با ۲٫۷۱۸۲۸) در آنالیز ریاضی لگاریتم در پایهٔ عدد e بسیار کاربرد دارد، لگاریتم در پایهٔ ۱۰ را میتوان بوسیلهٔ ماشین حسابهای دستی که در اختیار است به آسانی محاسبه کرد:[۴]

لگاریتم در پایهٔ ۱۰ را میتوان به آسانی با شمردن تعداد رقمهای یک عدد بدست آورد. برای نمونه (۱۴۳۰) log۱۰ تقریبا برابر است با ۳٫۱۵ چون ۱۴۳۰ چهار رقم دارد پس لگاریتم آن در پایهٔ ۱۰ باید عددی میان ۳ و ۴ باشد. لگاریتم در پایهٔ ۲ در علوم رایانه مورد استفاده قرار میگیرد چون در آن از دستگاه اعداد دودویی استفاده میشود.
جدولی که در ادامه قرار داده شدهاست علامتهایی که برای نشان دادن تابع لگاریتم کاربرد دارند و جایی که هر نوع لگاریتم مورد استفاده قرار میگیرد را نشان دادهاست. در بسیاری موارد اگر بتوان از روی نوشته تشخیص داد تنها از نماد لگاریتم استفاده میکنند و از نوشتن پایهٔ آن خودداری میکنند. در جدول زیر نمادی ستون «نماد ISO» مربوط به پیشنهادی است که از سوی سازمان بینالمللی استانداردسازی[۵] داده شدهاست.(ISO 31-11)
| پایهٔ b | نام گونهٔ لگاریتم | ISO نماد در | دیگر نمادها | کاربرد |
|---|---|---|---|---|
| ۲ | لگاریتم دودویی | lb(x)[۶] | ld(x)، log(x) (در علوم رایانه)، lg(x) |
علوم رایانه، نظریهٔ اطلاعات |
| e | لگاریتم طبیعی | ln(x)[nb ۲] | log(x) (در ریاضی و بسیاری از زبانهای برنامه نویسی[nb ۳]) |
آنالیز ریاضی، فیزیک، شیمی آمار, علم اقتصاد, و بعضی از زمینههای مهندسی |
| ۱۰ | لگاریتم اعشاری | lg(x) | log(x) (در مهندسی، زیست شناسی، اخترشناسی), |
در زمینههای گوناگون مهندسی (مانند دسیبل)، تهیه جدول لگاریتم و ماشین حسابهای مهندسی |
مطالب مشابه :
لگاریتم (2)
روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio
لگاریتم
برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را
لگاريتم
لگاریتم: یک عدد در یک پایه، توانی از پایه است که برابر آن عدد است. تابع لُگاريتم معکوس تابع
لگاریتم (1)
لُگاریتم یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه
تابع لگاریتمی
توابع لگاریتم در پایه می دانیم که اگر عدد مثبتی به جز یک باشد، تابع مشتق پذیر و یک به یک است.
لگاریتم
پگاه ریاضی - لگاریتم - لذت ریاضی را با مهران تجربه کنید
برچسب :
لگاریتم
