بیضی کیست ؟؟؟ چیست ؟؟؟ مساحتش چیست ؟؟؟
در هندسه، یک بیضی یک خم مسطح (خمی که در یک صفحهٔ اقلیدوسی تشکیل شدهاست.) است که از برخورد یک صفحه با یک مخروط ایجاد میشود به شرطی که خم ایجاد شده بسته باشد. برابر انگلیسی واژهٔ بیضی، ellipse از واژهٔ یونانی ἔλλειψις elleipsis به معنی falling short گرفته شدهاست. دایره حالت خاص بیضی است؛ که هنگامی بدست میآید که صفحهٔ عمود بر محور مخروط با آن برخورد کرده باشد. تعریف دیگر بیضی عبارت است از: مکان هندسی نقاطی از صفحهاست که مجموع فاصلههای آنها از دو نقطهٔ ثابت به یک اندازه ثابت مثبت باشد.
بیضیها خمهای بسته و محدود از مقطع مخروط اند، این خمها از برخورد یک مخروط دایرهای با یک صفحه که از رأس مخروط نمیگذرد تشکیل شدهاند. دو نوع خم دیگر نیز از برخورد صفحه با مخروط میتوانند ایجاد شوند، این خمها همگی باز اند و تشکیل سهمی و هذلولی میدهند.
در تعریفی دیگر بیضی مکان هندسی نقاطی است که نسبت فاصله آن از یک نقطه (کانون بیضی)، به فاصله آن از یک خط (خط هادی) برابر با عددی ثابت و کوچکتر از یک است.
اجزای بیضی
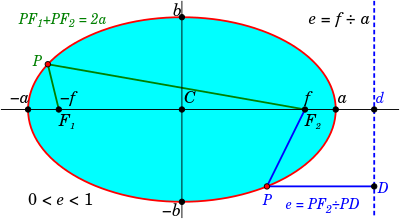
 یک بیضی و برخی ویژگیهای ریاضی آن.
یک بیضی و برخی ویژگیهای ریاضی آن.
یک بیضی یک خم بستهاست که نسبت به محورهای عمودی و افقی خود متقارن است. دو نقطه بر روی محیط بیضی که در دو سوی مخالف هم قرار دارند، یا به بیان دیگر، دو نقطه که خط واصل میان آنها از مرکز بیضی عبور میکند هنگامی در دورترین فاصله نسبت به هم قرار دارند که بر روی قطر بزرگ بیضی یا محور تقارن بزرگتر بیضی قرار گرفته باشند؛ و هنگامی کمترین مقدار را دارد که آن دو نقطه بر روی محور عمود بر قطر بزرگ، یعنی محور تقارن کوچکتر یا قطر کوچک بیضی قرار گرفته باشند.[۱]
نیمقطر بزرگ (که در شکل با a نمایش داده شدهاست) و نیمقطر کوچک بیضی (که در شکل با b نمایش داده شدهاست) به ترتیب نیمی از قطر بزرگ و نیمی از قطر کوچک بیضی اند که گاهی به آنها شعاع کوچک (major radius) و شعاع بزرگ (minor radius) نیز میگویند.
همچنین در انگلیسی به آنها major semi-axes و minor semi-axes نیز گفته میشود.
محیط بیضی
محیط بیضی به کمک انتگرالهای کامل بیضوی نوع دوم قابل محاسبهاست. البته فرمول صریحی همانند مساحت بیضی که برابر A = πab میباشد برای محیط بیضی وجود ندارد. و محیط بیضی تنها بوسیلهٔ سری نامتناهی قابل محاسبهاست:
![C = 2\pi a \left[{1 - \left({1\over 2}\right)^2\varepsilon^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{\varepsilon^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{\varepsilon^6\over5} - \dots}\right]\,\!](http://www.bargozideha.com/static/portal/28/287312-361917.png)
یا

در روابط فوق ε خروج از مرکز بیضی است. در ضمن خروج از مرکزیت بیضی برابر با فاصلهٔ دو کانون تقسیم بر قطر اطول(2a) میباشد.
حروف مرتبط : بیضی / اولین فرمول مساحت بیضی / مساحت بیضی / بیضی چیست / انتگرال بیضی / محیط بیضی /
مطالب مشابه :
مساحت ، محیط و حجم شکلهای هندسی
ریاضیات و هندسه - مساحت ، محیط و حجم شکلهای هندسی - مروارید علوم مساحت بیضی برابر است با :
بیضی کیست ؟؟؟ چیست ؟؟؟ مساحتش چیست ؟؟؟
حروف مرتبط : بیضی / اولین فرمول مساحت بیضی / مساحت بیضی / بیضی چیست / انتگرال بیضی / محیط بیضی / .:
حجم ومساحت اشکال هندسی /ریاضی ششم
مساحت بیضی = مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحت قاعده ×
مساحت ، محیط و حجم شکل های هندسی
مهندس کوچولو - مساحت ، محیط و حجم شکل های هندسی - علمی - آموزشی - درسی = مساحت بیضی.
محیط و مساحت اشکال هندسی
کلاس ریاضی - محیط و مساحت اشکال هندسی مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3
محیط و مساحت بیضی
به دنبال مساحت و محیط بیضی هر چی توی اینترنت گشتم چیزی ندیدم ولی یادم افتاد که یه زمانی درسش
برچسب :
مساحت بیضی
