نظریه گراف
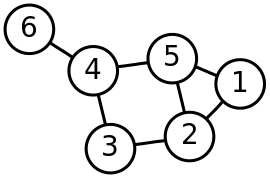
نظریه گراف شاخهای از ریاضیات است که دربارهٔ گراف ها بحث میکند. به صورت شهودی، گراف نموداری است، شامل تعدادی رأس، که با یالهایی به هم وصل شدهاند.
فهرست مندرجات
|
تعریف
تعریف دقیقتر گراف به این صورت است، که گراف مجموعهای از رأسها است، که توسط خانوادهای از زوجهای مرتب که همان یالها هستند به هم مربوط شدهاند.
یالها بر دو نوع ساده و جهت دار هستند، که هر کدام در جای خود کاربردهای بسیاری دارد. مثلاً اگر صرفاً اتصال دو نقطه -مانند اتصال تهران و زنجان با کمک آزادراه- مد نظر شما باشد، کافیست آن دو شهر را با دو نقطه نمایش داده، و اتوبان مزبور را با یالی ساده نمایش دهید. اما اگر بین دو شهر جادهای یکطرفه وجود داشته باشد آنگاه لازمست تا شما با قرار دادن یالی جهت دار مسیر حرکت را در آن جاده مشخص کنید.
آغاز نظریهٔ گراف به سدهٔ هجدهم بر میگردد. اولر ریاضیدان بزرگ مفهوم گراف را برای حل مسئله پلهای کونیگسبرگ ابداع کرد اما رشد و پویایی این نظریه عمدتاً مربوط به نیم سدهٔ اخیر و با رشد علم انفورماتیک بودهاست.
مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد و یا الگوریتمهای مناسب مانند الگوریتم دایسترا یا الگوریتم کروسکال و ... را بر روی آن اعمال نمود.
یکی از قسمتهای پرکاربرد نظریهٔ گراف، گراف مسطح یا هامنی است که به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل راسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مساله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود.
نظریه گراف یکی از پرکاربردترین نظریهها در شاخههای مختلف علوم مهندسی (مانند عمران)، باستانشناسی (کشف محدوده یک تمدن) و ... است.
روابط میان راس های یک گراف را می توان با کمک ماتریس بیان کرد .
انواع گراف
گراف ساده: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از تمام زیرمجموعههای دو عضوی V میباشد. اعضای V را رأسهای G و اعضای E را یالهای G مینامیم. به بیان ساده تر بین دو رأس یک گراف ساده حداکثر یک یال وجود دارد.
گراف چندگانه: هرگاه بین دو رأس متمایز از یک گراف بیش از یک یال وجود داشته باشد، آن را یک گراف چند گانه میگوییم.
گراف جهت دار: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از مجموعهٔ تمام زوج مرتبهای متشکل از اعضای V است.
گراف مسطح: گراف مسطح گرافی است که می توان آن را در یک صفحه محاط کرد به گونه ای که یال هایش یکدیگر را تنها در راس ها قطع کنند.
خصوصیات گرافهای خاص
- اگر تعداد یالها و درجهٔ راسها در گراف ساده برابر باشد، گراف مورد نظر منتظم کامل است. در این گونه گراف ها، رابطهٔ میان رأسها و یالها چنین است:
 که در آن
که در آن  تعداد راسها، و
تعداد راسها، و  تعداد یالها است.
تعداد یالها است. - اگر گراف همبند باشد (یعنی از هر نقطه بتوان به یک نقطه دلخواه دیگر رسید) ولی دور نداشته باشد (یعنی هیچ نقطهای از دوراه به نقطهٔ بعدی نرسد) می گویند گراف درختی است. فرمول آنهم این چنین است:
 که در آن
که در آن  تعداد رأسها، و
تعداد رأسها، و  تعداد یالها است.[۱]
تعداد یالها است.[۱]- گراف اویلری و همیلتونی:گاهی اوقات ما می خواهیم در یک گراف حرکت کنیم.به اینصورت که از راسی به راسی دیگر برویم.در اینصورت ممکن است برای ما مهم باشد که از روی یال یا راس تکراری حرکت نکنیم(مشابه مساله ی فروشنده ی دوره گرد).این مساله در صرفه جویی زمان و هزینه هم مهم است.(یعنی مبحث بهینه سازی).دراینجا دو موضوع گرافهای اویلری(دور زدن در گراف بدون یال تکراری)و همیلتونی(دور زدن بدون راس تکراری) مطرح میشود.براحتی میتوان بررسی کرد که راسهای گراف اویلری باید درجه ی زوج داشته باشند.اما اینکه شرایط کامل لازم و کافی برای همیلتونی بودن یک گراف چیست هنوز حل نشده مانده است.
مطالب مشابه :
دانلود رایگان نظریه گراف و کاربردهای آن
دانشکده فنی و حرفه ای سما فیروزاباد - دانلود رایگان نظریه گراف و کاربردهای آن - دانشکده فنی و
نمونه سوالات درس « نظریه گراف و کاربردهای آن »+همراه پاسخنامه
اخبار پیام نور - نمونه سوالات درس « نظریه گراف و کاربردهای آن »+همراه پاسخنامه | اخبار پیام
نمونه سوال نظریه گراف و کاربردهای آن پیام نور کلیه گرایش ها 91-90
مولا علی جان (ع) : ستایش مخصوص خدایی است که سزاوار ستایش است. از آنِ اوست رساترین ستایش و
نظریه گراف
نظریه گراف شاخهای از در جای خود کاربردهای کروسکال و را بر روی آن
نمونه سوال نظريه گراف و كاربردهاي آن
به درخواست دوستان دو نمونه سوال از درس "نظريه گراف و كاربردهاي آن" رو روي وبلاگ قرار دادم و
تاریخچه نظریه گرافها
نیز می توانیم تیم های ورزشی را در نظر بگیریم و آن و نظریه گراف و می توان کاربردهای
کاربرد نظریه گراف
کاربرد نظریه گراف الگوریتم کروسکال و را بر روی آن میشود که کاربردهای
بارم بندی جدید ریاضیات گسسته چهارم ریاضی
فصل1: گراف ها و کاربردهای آن: 2: فصل2: نظریه اعداد: 11: فصل2: نظریه
روش مطالعه گسسته
فصل اول: گراف و کاربردهای آن در این فصل، مطالب زیر مورد بررسی قرار گرفته است: نظریه اعداد
لیست جدید ارائه دروس مهندسی فناوری اطلاعات(طرح تجمیع)
اضافه شدن درس نظریه گراف و کاربردهای آن به دروس اختیاری (پیش نیاز: ساختمان گسسته)
برچسب :
نظریه گراف و کاربردهای آن