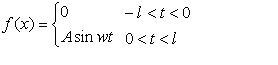سری فوریه

سری فوریه

فرض کنید تابع f به صورت زیر تعریف شده یاشد.

تابع f یک تابع تناوبی با دوره 2L می باشد و ثابتهای بسط فوریه این تابع از روایط زیر بدست می آیند

برای محاسبه این ثوابت از دستور int استفاده می کنیم

R = int(S)
R = int(S,v)
R = int(S,a,b)
R = int(S,v,a,b)

استفاده از این دستور ببسیار ساده است.S عبارتی است که می خواهیم از آن انتگرال بگیریم، v متغیر مستقل است و a,b حدود انتگرال گیری هستند

اولین قدم برای استفاده از این دستور تعریف متغیرهاست

syms w A t n

و بعد از آن محاسبه ثوابت

a0= w/pi*int('A*sin(w*t)','t',0,pi/w)

an=w/pi*int('A*sin(w*t)*cos(n*w*t)','t',0,pi/w)

bn=w/pi*int('A*sin(w*t)*sin(n*w*t)','t',0,pi/w)

قدم بعدی یافتن مقدار ثوابت در n های مختلف است.برای این کار از دستور subs استفاده می کنیم

subs(bn,n,3)

دستور بالا مقدار bn را به ازای n=3 محاسبه می کند

مقدار an را در n=1 مبهم است چون صورت و مخرج an صفر می شود .با استفاده از دستور limit حد این عبارت را در n=1 می توان بدست آورد.

limit(an,n,1,'right')

limit(an,n,1,'left')

حتما می دانید که سری فوریه هر تابع، تقریبی از آن تابع است.هرچه چملات سری بیشتر باشد مقدار سری به مقدار واقعی تابع نزدیک تر است.

یکی از راه های بدست آوردن سری فوریه یک تابع استفاده از دستور fit است.این دستور توانایی محاسبه سری فوریه با حداکثر 8 جمله را دارد.

x=[-pi:.1:pi]';

y=sin(x);

f=fit(x,y,'fourier1')

به جای fourier1 می توان fourier2...fourier8 را قرار داد.

توابع زیر هم نیاز معرفی ندارند/

تابع گاما

Y = gamma(A)

تابع خطا

Y = erf(X)

تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک انتقال انتگرالی است که هر تابع f(t) را به یک تابع دیگر F(ω) منعکس می‌کند. به F(ω) در این صورت تبدیل‌شده فوریه تابع f(t) می‌گویند. حالت خاص انتقال فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع f(t) متناوب باشد، یعنی: f(t + T) = f(t) . حال اگر تابع متناوب نباشد و یا به عبارتی، تناوب آن برابر بی‌نهایت باشد ( $T\to\infty$ )، آنگاه از سری فوریه به راحتی، عبارت زیر به دست می‌آید: