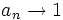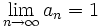دنباله وهمگراي
دنباله و همگرایی
حال مجموعه اعداد طبیعی را در نظر بگیرید:  با کمی دقت متوجه میشویم که میتوان یک تابع یک به یک از مجموعه اعداد طبیعی
به مجموعه اعداد طبیعی زوج تعریف نمود که در عضو از مجموعه اعداد طبیعی را
به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.(مانند شکل)
با کمی دقت متوجه میشویم که میتوان یک تابع یک به یک از مجموعه اعداد طبیعی
به مجموعه اعداد طبیعی زوج تعریف نمود که در عضو از مجموعه اعداد طبیعی را
به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.(مانند شکل) 
اگر این تناظر را به صورت مجموعه زوج های مرتب بنویسیم خواهیم داشت:  متوجه میشویم تابع
f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، تابعی است یک به یک
که هر عضو از دامنه خود را دو برابر میکند و به یک عضو از مجموعه اعداد
طبیعی زوج متناظر میکند و میتوان چنین ضابطهای برای آن تعیین نمود:
متوجه میشویم تابع
f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، تابعی است یک به یک
که هر عضو از دامنه خود را دو برابر میکند و به یک عضو از مجموعه اعداد
طبیعی زوج متناظر میکند و میتوان چنین ضابطهای برای آن تعیین نمود: 
حال در مثالی دیگر تابع  را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:
را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم: 
مشاهده
میکنید این تابع نیز هر عدد طبیعی را به عنوان ورودی دریافت میکند و آن
را به یک عدد دیگر نسبت میدهد با این تفاوت که این تابع دیگر یک به یک
نمیباشد و فقط بین اعداد طبیعی و مجموعه اعداد حقیقی یک تناظر بوجود
میآورد.
نمونه های دیگری نیز از این توابع وجود دارد مثلاً توابع  ،
،  ، که در آنها n عددی طبیعی است.
، که در آنها n عددی طبیعی است.
به چنین توابعی که از از مجموعه اعداد طبیعی به یک مجموعه دیگر تعریف میشوند دنباله میگوییم. در دنباله اعداد طبیعی زوج، عدد 2 از برد تابع
را جمله اول، عدد 4 را جمله دوم و به همین ترتیب عدد 2n را جمله n ام
دنباله میگوییم. همین شیوه برای سایر دنبالهها نیز اعمال میشود.
در
یک دنباله، اعداد طبیعی در دامنه به گونهای به اعضای برد متناظر میشوند
که عدد طبیعی متناظر شده بیانگر شماره آن جمله در برد باشد به عنوان مثال
در دنباله اعداد طبیعی زوج، عدد 1 در دامنه به عدد 2 در برد که اولین جمله
دنباله است متناظر میشود و عدد 10 از دامنه به عدد 20 از برد که جمله دهم
است متناظر میشود و به همین ترتیب عدد n در دامنه به عدد 2n از برد که
جمله n ام است متناظر می شود.
تعریف دنباله
دنباله (sequence) تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. پس در حالت کلی یک دنباله چون f تابعی است از مجموعه اعداد طبیعی به یک مجموعه دیگر چون A.

اگر دامنه دنباله قطعه ای از مجموعه اعداد طبیعی باشد دنباله را متناهی میگوییم و اگر دامنه دنباله خود مجموعه اعداد طبیعی باشد دنباله را نامتناهی میگوییم. به عنوان مثال دنباله اعداد طبیعی زوج کوچکتر از 10 یک دنباله متناهی است چرا که دامنه آن قطعه ای از مجموعه اعداد طبیعی یعنی
 است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.
است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است. برای مشخص کردن یک دنباله مانند هر تابع دیگر باشد دامنه و ضابطه آن را مشخص کرد. ضابطه یک دنباله را در اصطلاح جمله عمومی آن دنباله میگوییم. اگر f یک دنباله باشد جمله عمومی آن را با (f(n و یا به صورتی معمولتر به صورت
 نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد
نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد  استفاده میکنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم:
استفاده میکنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم: 
برای نمایش خود دنباله از نماد
 استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:
استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:

دنباله حقیقی
دنباله
 را دنباله حقیقی میگویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد به عبارت دیگر تابع
را دنباله حقیقی میگویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد به عبارت دیگر تابع را یک دنباله حقیقی میگویند.
را یک دنباله حقیقی میگویند. به عنوان مثال دنباله
 دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.
لازم به توضیح است معمولاً منظور از دنباله، دنباله حقیقی است.
دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.
لازم به توضیح است معمولاً منظور از دنباله، دنباله حقیقی است. نمودار یک دنباله
از آنجا که دنباله یک تابع با دامنه عداد طبیعی است میتوان دنباله را بوسیله نمودار نیز نمایش داد. این نمایش با دو روش انجام میشود. در یک روش میتوان مانند توابع دیگر آن را در دستگاه مختصات دکارتی رسم کرد و در روشی دیگر میتوان جملات آن را به همراه ذکر شماره آن جمله روی محور اعداد نشان داد. با ذکر یک مثال دو روش را توضیح میدهیم. به عنوان مثال میخواهیم دنباله اعداد زوج را به هر دو روش نشان دهیم:
- بوسیله رسم نمودار در دستگاه مختصات دکارتی: برای این منظور محور افقی را برای متغیر انتخاب کرده و محور عمودی را برای نمایش تغییرات جملات دنباله استفاده میکنیم. نمودار این دنباله به این صورت خواهد بود:

- بوسیله رسم نمودار روی محور اعداد: برای این منظور روی محور اعداد مقدار جملات دنباله را یافته و شماره جمله را در بالا آن مینویسیم مانند این نمودار:

جمله عمومی یک دنباله
همانطور که گفته شد یک دنباله تابعی با دامنه مجموعه اعداد طبیعی است پس برای دنباله ها در حالت کلی میتوان ضابطه تعیین کرد که به ضابطه یک دنباله جمله عمومی آن دنباله میگویند. جمله عمومی یک دنباله به منزله یک قانون است که بوسیله آن هر عضو از دامنه(مجموعه اعداد طبیعی) به یک عضو از مجموعه برد متناظر میشود و به ازای هر مقدار از متغیر n، جملات دنباله را تولید میکند.
به عنوان مثال جمله عمومی دنباله اعداد طبیعی زوج به صورت
 است که همانند ضابطه تابع بوسیله آن میتوان با قرار دادن هر n طبیعی جمله n ام
است که همانند ضابطه تابع بوسیله آن میتوان با قرار دادن هر n طبیعی جمله n ام  را بدست آورد.
را بدست آورد. البته لازم به ذکر است همه دنبالهها دارای جمله عمومی نمیباشند. به عنوان مثال تا کنون جمله عمومی برای دنباله اعداد اول تعیین نشده است. همچنین ممکن است یک سری از اعداد را به عنوان جملات دنباله انتخاب نمود که نتوان میان آنها رابطه ای برقرار نمود و جمله عمومی برای آنها نوشت.
حال ممکن است این سوال پیش بیاید که آیا با در اختیار داشتن جملات یک دنباله می توان جمله عمومی آن را تعیین کرد؟
پاسخ را با یک مثال بررسی میکنیم. دنباله زیر را در نظر بگیرید:

میخواهیم جمله عمومی این دنباله را با توجه به جملاتش تعیین کنیم.
با مشاهدهی جملات ممکن است حدس شما این باشد که این دنباله، دنباله اعداد طبیعی فرد بزرگتر از یک است و جمله عمومی آن را میتوان به این صورت نوشت:

اما این ممکن است یک جمله عمومی برای این دنباله باشد. ممکن است جملات دنباله در ادامه به این روال پیش نروند
و جمله چهارم این دنباله عددی چون 9 نباشد! چرا که ما از جمله سوم به بعد دنباله هیچ اطلاعی نداریم و هر عدد دیگری نیز میتواند باشد!
به عنوان مثال جمله عمومی دنباله فوق را میتوان به این صورت نوشت:

با نوشتن جملات این دنباله داریم:

مشاهده میکنید جملات این دنباله تا جمله سوم همانند دنباله
 است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند.
است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند. پس همواره از روی جملات یک دنباله نمیتوان جمله عمومی آن را به درستی تعیین کرد. اما معمولاً برای نوشتن جمله عمومی یک دنباله با توجه به جملات آن، ساده ترین حالت را در نظر میگیریم. لذا جمله عمومی
 برای این دنباله صحیحتر است و زودتر به ذهن خطور میکند.
برای این دنباله صحیحتر است و زودتر به ذهن خطور میکند. رابطه بازگشتی و دنباله بازگشتی
به دنباله اعداد زوج دقت کنید: ...,2,4,6,8,10,12
با کمی دقت در مییابید که برای بدست آوردن هر جمله کافی است جمله قبل را با عدد دو جمع کنید. به عنوان مثال برای بدست آوردن جمله پنجم(10) کافی است جمله چهارم(8) را با عدد دو جمع کنید. به این رابطه که بین جملات این دنباله برقرار است رابطه بازگشتی می گوییم.
- تعریف: در بسیاری از دنبالهها بین هر جمله و جملات ماقبل یک رابطهای وجود دارد که بوسیله آن میتوان جملات بعدی را تعیین نمود. به چنین رابطهای، رابطه بازگشتی میگوییم و به دنبالههایی با این رابطه، دنباله بازگشتی میگوییم.
به عنوان مثال دنباله فیبوناتچی دارای چنین رابطهای است که بوسیله آن مشخص میشود:

که جملات آن به این صورت است: ...,1,1,2,3,5,8,13,21
مشاهده میشود برای بدست آوردن هر جمله از جمله دوم به بعد کافی است دو جمله ماقبل آن جمله را با هم جمع کنیم. مثلا برای محاسبه جمله نهم داریم:

از آنجا که دنباله نیز تابع میباشد میتوان حد آن را نیز بررسی کرد. در ادامه مطلب می توانید اطلاعاتی در مورد همگرایی دنباله ها را مطالعه کنید.
مفهوم شهودی حد دنباله
دنباله
 را درنظر بگیرید. چند جمله اول این دنباله به این صورت است:
را درنظر بگیرید. چند جمله اول این دنباله به این صورت است: 
ملاحضه میکنید جملات این دنباله رفته رفته به عدد یک نزدیک میشوند. کار را ادامه بدهید و جملات را افزایش بدهید:








خوب تا اینجا به صورت شهودی، متوجه میشویم که هر چه بیشتر جلو میرویم و تعداد جملات (n) را افزایش میدهیم مقدار دنباله به عدد 1 نزدیک و نزدیکتر میشود (لااقل تا الان که اینطور بوده است!). حال ممکن است این سوال پیش بیاید که آیا میتوانیم حکمی کلی صادر کنیم و بگویم به طور کلی هرچه تعداد جملات را افزایش بدهیم جملات دنباله به عدد 1 نزدیک و نزدیکتر میشوند یا به عبارت دیگر میتوان جملات دنباله را به هر مقدار دلخواه به عدد 1 نزدیک کرد به شرط اینکه مقدار n به قدر کافی بزرگ باشد؟
مثلا اگر ما n را برابر 1000000 قرار دهیم مقدار دنباله
 بدست میآید و اگر n را 1000000000000 انتخاب کنیم مقدار دنباله برابر خواهد بود با عدد
بدست میآید و اگر n را 1000000000000 انتخاب کنیم مقدار دنباله برابر خواهد بود با عدد  که مقداری بسیار نزدیک به 1 است. آیا میتوان با اطمینان گفت با انتخاب n
مناسب میتوان بیشتر و بیشتر به 1 نزدیک شد و تقریبهای نزدیکتر به عدد 1
بدست آورد؟
که مقداری بسیار نزدیک به 1 است. آیا میتوان با اطمینان گفت با انتخاب n
مناسب میتوان بیشتر و بیشتر به 1 نزدیک شد و تقریبهای نزدیکتر به عدد 1
بدست آورد؟ خوب پس در اینجا با یک حدس روبرو هستیم که باید آن را ثابت یا رد کنیم، و آن این است که دنباله
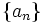 را به هر میزان میتوان به 1 نزدیک کرد به شرط اینکه n به قدر کافی بزرگ انتخاب شده باشد. بیاید با هم سعی در اثبات این حدس کنیم.
را به هر میزان میتوان به 1 نزدیک کرد به شرط اینکه n به قدر کافی بزرگ انتخاب شده باشد. بیاید با هم سعی در اثبات این حدس کنیم. اولین قدم برای اثبات این است که سعی کنیم مسئله را به زبان ریاضی (صوری) بنویسیم که بتوانیم آن را از نظر ریاضی بهتر بررسی کنیم. در واقع بیان ریاضی حدس ما این است که اگر ما هر همسایگی دلخواه از عدد 1 را در نظر بگیریم مانند
 (که اپسیلون عددی حقیقی مثبت و لخواه است)، بالاخره بهازای یک N ای جملات دنباله
(که اپسیلون عددی حقیقی مثبت و لخواه است)، بالاخره بهازای یک N ای جملات دنباله 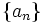 از این به بعد (از این N به بعد) در این همسایگی قرار میگیرند یعنی بالاخره برای هر
از این به بعد (از این N به بعد) در این همسایگی قرار میگیرند یعنی بالاخره برای هر  یک N ای از اعداد طبیعی وجود دارد که برای n>N داریم:
یک N ای از اعداد طبیعی وجود دارد که برای n>N داریم:

به عنوان مثال اگر همسایگی
 را انتخاب کنیم (یعنی اپسیلون را 0.01 بگیریم) برای n>1000 خواهیم داشت:
را انتخاب کنیم (یعنی اپسیلون را 0.01 بگیریم) برای n>1000 خواهیم داشت:  یعنی از جمله 1000ام به بعد همه جملات دنباله در این همسایگی قرار میگیرند. زیرا ، n>1000 و لذا داریم
یعنی از جمله 1000ام به بعد همه جملات دنباله در این همسایگی قرار میگیرند. زیرا ، n>1000 و لذا داریم  و در نتیجه:
و در نتیجه: 
پس در اینجا N مورد نظر N=1000 است که از این جمله به بعد جملات دنباله در همسایگی مورد نظر قرار میگیرند. پس حالا متوجه شدیم که برای اثبات حکم باید چکار کنیم. هدف ما این است که تحقیق کنیم آیا این N همواره برای هر همسایگی دلخواه (یا به عبارتی برای هر اپسیلون) وجود دارد یا نه؟
لذا با یک قضیه وجودی روبرو هستیم یعنی برای اثبات این قضیه کافی است برای هر همسایگی دلخواه از 1 مانند
 (که اپسیلون عددی حقیقی و مثبت است) یک N از اعداد طبیعی را معرفی کنیم که برای n>N داشته باشیم:
(که اپسیلون عددی حقیقی و مثبت است) یک N از اعداد طبیعی را معرفی کنیم که برای n>N داشته باشیم: 
پس فرض میکنیم
 عددی حقیقی مثبت دلخواهی باشد (با این فرض در حقیقت یک همسایگی دلخواه از 1
را انتخاب کردیم)، سعی میکنیم برای این اپسیلون یک N ای از اعداد طبیعی
پیدا کنیم که n>N نامساوی
عددی حقیقی مثبت دلخواهی باشد (با این فرض در حقیقت یک همسایگی دلخواه از 1
را انتخاب کردیم)، سعی میکنیم برای این اپسیلون یک N ای از اعداد طبیعی
پیدا کنیم که n>N نامساوی  را
ایجاب کند. خوب از اینجا به بعد باید به دنبال یک N بگردیم و یافتن N به
ابتکار شما و مهارتهای ریاضی شما بستگی دارد. ببینیم میتوانیم با ایجاد
تغییراتی در حکم، ایدهای برای معرفی N مناسب بگیریم یا نه؟ ما میخواهیم N
مناسب طوری باشد که n>N ایجاب کند
را
ایجاب کند. خوب از اینجا به بعد باید به دنبال یک N بگردیم و یافتن N به
ابتکار شما و مهارتهای ریاضی شما بستگی دارد. ببینیم میتوانیم با ایجاد
تغییراتی در حکم، ایدهای برای معرفی N مناسب بگیریم یا نه؟ ما میخواهیم N
مناسب طوری باشد که n>N ایجاب کند  ازاینجا داریم:
ازاینجا داریم: 


خوب با توجه به اینکه روابط فوق برگشت پذیر است متوجه میشویم که با استفاده هر عدد طبیعی بزرگتر از
 میتوان نامساوی
میتوان نامساوی  را نتیجه گرفت، یعنی
را نتیجه گرفت، یعنی  ایجاب میکند
ایجاب میکند  پس اگر ما یکی از اعداد طبیعی بزرگتر از
پس اگر ما یکی از اعداد طبیعی بزرگتر از  را به عنوان N مناسب معرفی کنیم حکم ثابت میشود. اما چه N ای؟
را به عنوان N مناسب معرفی کنیم حکم ثابت میشود. اما چه N ای؟ بیاید قرار دهیم
 که نماد
که نماد  نماد جزء صحیح است. بوضوح N ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز صحیح عددی بزرگتر از
نماد جزء صحیح است. بوضوح N ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز صحیح عددی بزرگتر از  است. پس یک N را پیدا کردیم و ادعا میکنیم این N همان N مناسبی است که n>N نامساوی
است. پس یک N را پیدا کردیم و ادعا میکنیم این N همان N مناسبی است که n>N نامساوی  را ایجاب میکند زیرا:
را ایجاب میکند زیرا: 


پس چون اپسیلون دلخواه بود N معرفی شده برای هر اپسیلون مناسب است. یعنی برای هر همسایگی دلخواهی از 1 که انتخاب کنیم مانند
 کافی است N را برابر
کافی است N را برابر  بگیریم که در این صورت جملات دنباله از این N به بعد همگی در همسایگی مورد
نظر ما قرار میگیرند. و به این ترتیب درستی حدس ما معلوم میشود. در
دنباله
بگیریم که در این صورت جملات دنباله از این N به بعد همگی در همسایگی مورد
نظر ما قرار میگیرند. و به این ترتیب درستی حدس ما معلوم میشود. در
دنباله 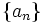 میتوانیم جملات دنباله را به اندازه دلخواه به 1 نزدیک کنیم به شرط اینکه
n را به اندازه کافی بزرگ اختیار کنیم. به بیان دیگر با افزایش n جملات
دنباله به 1 نزدیک و نزدیکتر میشوند.
میتوانیم جملات دنباله را به اندازه دلخواه به 1 نزدیک کنیم به شرط اینکه
n را به اندازه کافی بزرگ اختیار کنیم. به بیان دیگر با افزایش n جملات
دنباله به 1 نزدیک و نزدیکتر میشوند. - در این حالت میگوییم حد دنباله
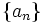 برابر است با 1و یا به صورتی رایجتر میگوییم دنباله به عدد 1 همگرا است و مینویسیم وقتی
برابر است با 1و یا به صورتی رایجتر میگوییم دنباله به عدد 1 همگرا است و مینویسیم وقتی 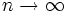 ، آنگاه
، آنگاه 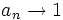 و یا به طور سادهتر
و یا به طور سادهتر 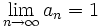 .
.
تعریف حد یک دنباله
دنباله
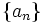 را دارای حد یا همگرا میگوییم هرگاه عددی حقیقی چون L موجود باشد به طوری که برای هر عدد حقیقی مثبت چون
را دارای حد یا همگرا میگوییم هرگاه عددی حقیقی چون L موجود باشد به طوری که برای هر عدد حقیقی مثبت چون  ، عددی طبیعی چون
، عددی طبیعی چون  موجود باشد که برای هر n>N داشته باشیم:
موجود باشد که برای هر n>N داشته باشیم: 
به عبارت دیگر میگوییم دنباله
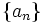 دارای حد L است یا به L همگرا است هرگاه:
دارای حد L است یا به L همگرا است هرگاه: 
در این حالت میگوییم دنباله
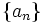 به L همگرا است و مینویسیم وقتی
به L همگرا است و مینویسیم وقتی 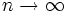 آنگاه
آنگاه  یا
یا  . به بیان سادهتر و کمی دورتر از عبارات صوری ریاضی، L حد دنباله
. به بیان سادهتر و کمی دورتر از عبارات صوری ریاضی، L حد دنباله 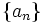 است اگر برای هر همسایگی دلخواه از L،
جملات دنباله از شمارهای به بعد (از یک N ای به بعد) در این همسایگی
دلخواه قرار بگیرند یا اینکه جملات دنباله را بتوان به قدر کافی به L نزدیک
کرد به شرط اینکه n به قدر کافی بزرگ باشد.
است اگر برای هر همسایگی دلخواه از L،
جملات دنباله از شمارهای به بعد (از یک N ای به بعد) در این همسایگی
دلخواه قرار بگیرند یا اینکه جملات دنباله را بتوان به قدر کافی به L نزدیک
کرد به شرط اینکه n به قدر کافی بزرگ باشد. همچنین میگوییم دنباله
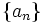 حد نامتناهی یا بینهایت دارد هرگاه:
حد نامتناهی یا بینهایت دارد هرگاه: 
به عبارت دیگر دنباله
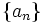 حد
نامتناهی یا بینهایت دارد هرگاه از یک شمارهای چون N به بعد جملات دنباله
از هرعدد حقیقی مثبت بزرگتر یا از هر عدد حقیقی منفی کوچکتر بشوند یعنی به
طور بی کران بزرگ یا کوچک شوند. در این حالت مینویسیم:
حد
نامتناهی یا بینهایت دارد هرگاه از یک شمارهای چون N به بعد جملات دنباله
از هرعدد حقیقی مثبت بزرگتر یا از هر عدد حقیقی منفی کوچکتر بشوند یعنی به
طور بی کران بزرگ یا کوچک شوند. در این حالت مینویسیم: 
با استفاده از تعریف فوق میتوانیم به اثبات قضایای حدود بپردازیم. روش اثبات همان روشی است که در قسمت قبلی از آن استفاده کردیم. حال به عنوان تمرین میخواهیم با استفاده از تعریف حد دنبالهها ثابت کنیم:

ابتدا حکم را مشخص میکنیم. میخواهیم نشان دهیم:

کافی است m مناسب را برای هر
 معرفی کنیم. بیاید مانند مثالی که قبلا بررسی کردیم سعی کنیم از حکم m مناسب را استخراج کنیم. با فرض
معرفی کنیم. بیاید مانند مثالی که قبلا بررسی کردیم سعی کنیم از حکم m مناسب را استخراج کنیم. با فرض  دلخواه و از این پس ثابت، m مطلوب ما m ای است که برای هر n>m داشته باشیم
دلخواه و از این پس ثابت، m مطلوب ما m ای است که برای هر n>m داشته باشیم  از اینجا داریم:
از اینجا داریم: 


اما نامساوی فوق برای هر
 برقرار نمیباشد (به عنوان مثال برای اپسیلون برابر با 3) پس m ای که ما
از این طریق بدست میآوریم برای ما مناسب نمیباشد پس با کمی در روش خود
تجدید نظر کنیم. برای این کار سعی میکنیم به نوعی نامساوی را تغییر دهیم.
داریم:
برقرار نمیباشد (به عنوان مثال برای اپسیلون برابر با 3) پس m ای که ما
از این طریق بدست میآوریم برای ما مناسب نمیباشد پس با کمی در روش خود
تجدید نظر کنیم. برای این کار سعی میکنیم به نوعی نامساوی را تغییر دهیم.
داریم: 
حال اگر m مناسب را از نامساوی جدید پیدا کنیم قطعاً برای نامساوی اصلی نیز مناسب خواهد بود (در واقع دلیل این مسئله این است که چیزی که برای ما مهم است نتیجه حاصل از برگشت این روابط است). با استفاده از نامساوی جدید داریم:

حال کافی است m را عددی طبیعی بزرگتر از
 اختیار کنیم مثلاً
اختیار کنیم مثلاً  حال ادعا میکنیم این همان m ای است که برای هر n>m داریم:
حال ادعا میکنیم این همان m ای است که برای هر n>m داریم: 
زیرا:




حال در قسمت بعدی به بررسی قضایای حد دنبالههای و نحوی محاسبه حدود دنبالهها میپردازیم.
قضایای حد دنبالهها
- قضیه1: حد یک دنباله در صورت وجود، منحصر بفرد است.
فرض میکنیم دنباله
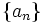 به
به  و
و  همگرا باشد(فرض خلف). چون
همگرا باشد(فرض خلف). چون داریم:
داریم: 
از طرفی چون
 داریم:
داریم: 
حال قرار میدهیم
 ، در این صورت برای هر n>m داریم
، در این صورت برای هر n>m داریم  و
و  که این دو باهم ایجاب میکنند:
که این دو باهم ایجاب میکنند: 
حال قرار میدهیم
 که در این صورت خواهیم داشت:
که در این صورت خواهیم داشت:

که این تناقض است. پس فرض خلف باطل و حکم برقرار است.
- قضیه 2: هر دنباله همگرا کراندار است.
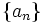 همگرا به L باشد. نشان م
همگرا به L باشد. نشان م
مطالب مشابه :
معرفی تابع قدر مطلق و خواص آن
در ریاضیات، قدر مطلق (Absolute Value) عددی حقیقی، مقدار عددی آن بدون در نظر گرفتن علامتش است.
ریاشی
تابع قدر مطلق و خواص قدر مطلق.
جلسه ی دوم (اعداد حقیقی - قدر مطلق - بازه ها)
ریاضیات مقدماتی و تخصصی - جلسه ی دوم (اعداد حقیقی - قدر مطلق - بازه ها) - مهدی مفیدی احمدی
فضیلت و خواص سوره قدر
سلوک عرفای اسلامی - فضیلت و خواص سوره قدر وب سایت حجت الاسلام سید عباس موسوی مطلق.
دنباله و همگرایی
بوضوح n ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز همچنین بنا به خواص قدر مطلق
توپولوژی با طعم ریاضیات ...
اين اعمال با خواص معين، R را به عنوان گروه، حلقه و (به عنوان نمونه R با متر قدر مطلق يعني| d
انواع تابع
در مورد خواص جبری ، برای توابع فرد این خاصیت جبری حاکم قدر مطلق عددی مانند x، عدد است.
دنباله وهمگراي
بوضوح n ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز همچنین بنا به خواص قدر مطلق
آموزش ریاضی/انواع تابع
در مورد خواص جبری ، برای توابع فرد این خاصیت جبری حاکم است که و یا که در آنها تابع قدر مطلق
دانلود جزوه کامل ریاضی رشته تجربی
مشتق تابع قدر مطلقی اکسترمم های مطلق خواص مشترک اکسترمم نسبی و عطف
برچسب :
خواص قدر مطلق