/تجربی ها و تهدید!!!/ سرشماری 6 /یک آدم فضایی/ک مثل کاوالیری/هندسه 1/ جواب مساله+تشکر/

<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

1) از خودمون

خیلی جای تعجب داره که خواهر آدم قالب نویس و مخ HTML باشه اما آدم یه قالب درست حسابی وبلاگش نداشته باشه!!! و بخواد تهدید های مکرر بعضیا رو در مورد قالب بشنوه!!!

*راستی بنده همین جا اعلام می کنم نتایج ششمین سرشماری ملی از اعتبار کافی برخور دار نیست! چون مامانم اینا همسایه ی طبقه ی پایینمونو جا انداختن!!!!

2) از خودمون و از ریاضی

و اما سوال پست پیش، با تشکر از آقای افشین منش (ریاضیات زیباست)و آقای اسماعیلی فر (لبخند ریاضی) بخاطر اثبات های قشنگی که کرده بودن... من فکر می کردم تعداد بیشتری به مساله جواب بدن!

جواب مساله:

الف) اثبات با استفاده از اصل لانه کبوتر

اگر در میهمانی کسانی را که دست می دهندn در نظر بگیریم و به کسانی که دست نمی دهند کاری نداشته باشیم هر نفر n-1 بار یا کمتر دست می دهد (چون با توجه به صورت سوال کسی با خودش دست نمی دهد... ) حالا اگر n نفر را کبوتر و تعداد دست دادن ها که n-1 حالت دارد: n-1), (n-2), (n-3),… , 1})} ، را لانه در نظر بگیریم طبق اصل لانه کبوتری حداقل دو نفر وجود دارند که تعداد دست دادن هایشان با هم برابر است.

ب) اثبات با کمک گراف

جواب دوستانمون اونقدر کامل بود که دیگه من هیچی نمی گم و جوابشونو براتون می نویسم.

آقای افشین منش: اگر درجه تمام روس زوج باشد که هیچ. (چون حتما دو راس با درجه مساوی خواهیم داشت- با توجه به نوع مساله).

اما اگر یک راس درجه فرد داشته باشیم آنوقت الزاما باید راس دیگری از درجه فرد وجود داشته باشد (زیرا تعداد رئوس با درجه فرد در یک گراف، عددی زوج است).

آقای اسماعیلی فر: اگر هر نفر رو یک راس بگیریم و هر دست دادن رو یک یال بین اونها اون وقت مساله گرافیکال میشه.

حالا چون تو این گراف طوقه نداریم(کسی با خودش دست نمیده) و این گراف چندگانه است(هیچ دو نفری دوبار یا بیشتر با هم دست نمی دهند) لذا گراف حاصل گراف ساده ست. تعداد دست دادن ها براي هر نفر هم معادل درجه گراف مفروضه.

قضیه: هر گراف ساده n راسي G، با حداقل دو راس داراي دو راس با درجه برابر است.

اثبات: مي دانيم درجه هر راس گراف G متعلق به مجموعه 0و1و ... n-1 است. اگر دو راس از درجه برابر باشند حكم برقرار است. در غير اينصورت (فرض خلف) همه اعداد فوق درجه راسي از گراف G خواهند بود (واضحه كه با اين فرض درجه هيچ دوراسي برابر نيست). مخصوصا اينكه دو راس وجود دارند كه يكي از درجه صفر و يكي از درجه n-1 است كه اين يه تناقضه(چون اگه يك راس درجه اش n-1 باشه اونوقت به همه رئوس ديگر يك يال داره و لذا درجه بقيه رئوس حداقل يك است و صفر بودن درجه يكي از رئوس با اين مطلبي كه بيان كرديم در تناقضه). پس فرض خلف باطل است و لذا دو راس وجود دارند كه از درجه برابرند.

حالا اگه معادل سوال شما رو بخوايم ازين قضيه نتيجه بگيريم داريم:

نتيجه: دو نفر وجود دارند كه تعداد دفعات دست دادنشان با يكديگر برابر است.

3) از ریاضی

نمی دونم تا حالا اسم کاوالیری به گوشتون خورده یا نه؟ من خودم هر وقت میگم یا می شنوم «کاوالیری» یاد آدم فضایی ها می افتم...!!!

ولی حتما از کتاب هندسه (1) یادتون هست، اون آخرای کتاب... خوب اگه دانش آموز این نظام آموزشین جای تعجب نداره!!!

«هندسه ی کاوالیری» موضوع این پسته. البته ابهام بوجود نیاد که هندسه ی کاوالیری یه نوع هندسه جدیده، یا یه هندسه ی نااقلیدسیه. این اسم رو من روش گذاشتم به معنی هندسه ای که کاوالیری با اون کار می کرد...

*هندسه یکاوالیری*

بوتاون تورا کاوالیری (1564-1642) اهل میلان، از همان سال های نخستین به ریاضیات علاقه مند بود،و به ظاهر زیر تاثیر گالیله، روش « غیر قابل تقسیم ها» را در هندسه بوجود آورد که در اثر بزرگ او در سال 1635، با عنوان «هندسه، با طرح تازه ای بر اساس غیر قابل تقسیم های پیوسته»، به شهرت رسید.

غیر قابل تقسیم ها، از نظر کاوالیری، وترهای موازی در درون شکل روی صفحه، و صفحه های موازی در درون جسم بود. او برای مقایسه ی شکل های روی صفحه و جسم های فضایی، مفهوم « مجموع همه ی غیر قابل تقسیم ها» را آورد که تماس سطح و فضای جسم را پر می کردند.

برای کاوالیری، نسبت این مجموع ها، همان نسبت مساحت ها و حجم ها بود. او شکل های روی صفحه را، بین دو خط راست موازی در نظر گرفت.

اصل کاوالیری درباره مساحت:

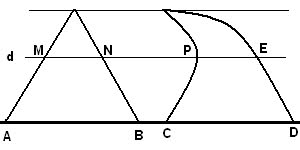
اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است.

با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند.

<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" />

اصل کاوالیری در باره حجم ها:

دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند.

خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتفاعشان برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.»

این نظام کار، به نام «نظام کاوالیری» معروف است.

کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها.

ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت.

طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن غیر قابل تقسیم ها، پیش در آمدی برای انتگرال گیری بود. کاوالیری نماد انتگرال را بکار نمی برد، ولی در واقع از انتگرال گیری استفاده می کرد...

به جز این، در هندسه ی کاولیری به قضیه هایی بر می خوریم که برای پیدایش محاسبه ی دیفرانسیلی، ارزش معینی دارند. از آن جمله، نخستین گزاره ای که در هندسه آمده، هم ارز با قضیه رول است، و به دنبال آن گزاره ای آمده است که مضمون آن اینست: در نقطه های ماکزیمم و می نیمم تابع، مماس بر نمودار با محور طول ها موازی است.

یکی از کمبود های جدی هندسه ی کاوالیری این است که مولف از بکارگیری جبر فراری است و همه جا به هندسه دانان قدیمی تکیه می کند. بی تردید، بکار گیری نمادهای جبری که در زمان کاوالیری رایج شده بود، می توانست کارهای او را دقیق تر، کامل تر و قابل درک تر کند.

تمام

/تجربی ها و تهدید!!!/ سرشماری 6 /یک آدم فضایی/ک مثل کاوالیری/هندسه 1/ جواب مساله+تشکر/

مطالب مشابه :

اصل کاوالیری

هندسه ی کاوالیری

/تجربی ها و تهدید!!!/ سرشماری 6 /یک آدم فضایی/ک مثل کاوالیری/هندسه 1/ جواب مساله+تشکر/

زندگینامه دانشمندان

لگاریتم (2)

قضیه ی دزارگ

تاریخچه ی ریاضیات

مباحث مهم آزمون 21 آذر قلم چی

آموزش کامل لگاریتم

هندسه یک – هندسه دو – هندسه تحلیلی