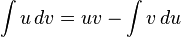انتگرال و دعوای نیوتن و لایب نیتز
اولین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.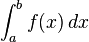
aو b نقاط ابتدا و انتهای بازه هستند و  تابعی انتگرالپذیر است و
تابعی انتگرالپذیر است و  نمادی برای متغیر انتگرال گیری است.
نمادی برای متغیر انتگرال گیری است.
از لحاظ تاریخی  یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است..
یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است..
از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.
نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سهگانه معرف پارالل زیر نمودار است(غیرقابل تصور).
مثال
انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی  است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.
است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.

 نمایش گرافیکی انتگرال.
نمایش گرافیکی انتگرال.
انتگرال یک تابع مساحت زیر نمودار آن تابع است.
انتگرال گیری
(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است.
مهمترین تعاریف در انتگرال
از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است. انتگرال ریمان بهوسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال ریمان-استیلچس (Riemann-Stieltjes) اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند:
محاسبه انتگرال
اکثر روشهای اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:
1.f تابعی در بازه (a,b) در نظر میگیریم. 2.پاد مشتق f را پیدا میکنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر میگیریم:
بنابراین مقدار انتگرال ما برابر خواهد بود.
به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه میدهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار سادهای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتاند از :
- انتگرال گیری بهوسیله تغییر متغیر
- انتگرال گیری جزء به جزء :
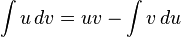
- انتگرال گیری با تغییر متغیر مثلثاتی
- انتگرال گیری بهوسیله تجزیه کسرها
روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار میرود همچنین میتوان بعضی از انتگرالها با ترفند هایی حل کرد برای مثال میتوانید به انتگرال گاوسی مراجعه کنید.
تقریب انتگرالهای معین
محاسبه سطح زیر نمودار بهوسیله مستطیل هایی زیر نمودار. هر چه قدرعرض مستطیلها کوچک میشوندمقدار دقیق تری از مقدار انتگرال بدست میآید.
انتگرال هایی معین ممکن است با استفاده از روشهای انتگرال گیری عددی، تخمین زده شوند.یکی از عمومیترین روشها، روش مستطیلی نامیده میشود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقهای است. اگر چه روشهای عددی مقدار دقیق انتگرال را به ما نمیدهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما میکند.
کاربرد
انتگرالها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک میتوان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست میآید. اما به طور کلی میتوان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیتها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته میشود:
![v=[L]/[T] t=[T] \!](http://www.bargozideha.com/static/portal/82/820089-773912.png)
سپس دو تحلیل را در هم ضرب می کنیم:
![[L] \!](http://www.bargozideha.com/static/portal/45/453665-271344.png)
پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.
جستارهای وابسته
دعوای نیوتن و لایب نیتز
در سال 1684 «لایب نیتس»با انتشار مقاله ای در باره حساب عناصر بی نهایت کوچک ، انقلابی برپا کرد. در این مقاله او برای توصیف یک پدیده پیچیده آن را به بی نهایت کوچک و ساده تقسیم کرد. مثلا یک منحنی را مرکب از بی نهایت پاره خط راست که بی نهایت کوچک و ساده بودند در نظر می گرفت و آن را به این وسیله توصیف می کرد.
«لایب نیتس» در این مقاله نشان داد که اگر می خواهید کمیتی مثل حرارت را مطالعه کنید که از مقداری معین تا مقداری دیگر تغییر می کند، باید نشان دهید این تغییرات از بی نهایت تغییر کوچک تشکیل شده. آن وقت باید آن بی نهایت تغییر کوچک را با هم جمع بزنید. او این تغییرات جزیی را دیفرانسیل و مجموع آنها را انتگرال نامید. وارد شدن حساب عناصر بی نهایت کوچک در قلمرو علم همچون هجوم توفان و یا موج مقاومت ناپذیری بود که به کلی دانش ریاضی را زیر و رو کرد. انتشار این مقاله باعث منازعه ای بزرگ در دنیای علم شد که تا به امروز پابرجاست.
«نیوتن» گوشه گیر
دعوای تاریخ علم حسابان از آنجا شروع شد که «ایزاک نیوتن» برای توزیع معادلات حرکت، به صورت جداگانه ای از «لایب نیتس» علم حساب دیفرانسیل و انتگرال را ابداع کرد. او کارش را زودتر از «لایب نیتس» شروع کرد اما انتشار زودتر مقاله «لایب نیتس»باعث شد که این ابداع به نام او ثبت شود. امروز می دانیم که «نیوتن» در بین سالهای 1664 تا 1666 روش حساب دیفرانسیل و انتگرال را اختراع کرد، اما میل همیشگی او برای پنهان کردن اکتشافاتش، باعث شد «لایب نیتس» که دیرتر از او شروع به مطالعه در این مورد کرده بود، زودتر مقاله اش را منتشر کند.
همین مساله باعث شد که «نیوتن»ادعا کند زودتر از «لایبنیتس»این معادلات را کشف کرده است و «لایب نیتس» معادلات او را دزدیده است. این منازعه آن قدر بالا گرفت تا هنگامی که «لایب نیتس» از آکادمی پادشاهی علوم انگلستان در خواست کرد، کمیتهای بی طرف برای بررسی این موضوع دست به کار شود، کمیته ای که رئیسش کسی نبود جز «نیوتن». او تعدادی از دوستان خود را برای این کار انتخاب کرد و در نتیجه «لایب نیتس» به دزدی محکوم شد. اما امروز می دانیم که آنها جداگانه این معادلات را صورت بندی کرده اند.
امروزه ریاضیدانان از علائم پیشنهادی «لایب نیتس» برای دیفرانسیل استفاده می کنند و در حالیکه فیزیکدانان به پشتیبانی از «نیوتن» علائم او را به کار می برند. این معادلات برای توصیف دقیق ریاضی از پدیده ها و اتفاقات فیزیکی و غیرفیزیکی کاربرد دارند.
مطالب مشابه :
انتگرال ریمان
دریای ریاضی - انتگرال ریمان - آموزش ریاضی، دانلود رایگان جزوه های دانشگاهی،کتاب های
انتگرال ریمان
انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته میشود.
انتگرال ریمان
ریاضیات دبیرستان - انتگرال ریمان - - ریاضیات دبیرستان این وبلاگ برای تمامی علاقمندان به
انتگرال
از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است.
اندازه و انتگرال لبگ
انتگرال لبگ (Lebesgue این انتگرال، دسته ی عظیمی از توابع انتگرالپذیر که انتگرال ریمان (Riemann
انتگرال
انتگرال معین بنا به تعریف، نماد را انتگرال معین نامیده و حاصل آن را به ازای عددی به صورت زیر
انتگرال و دعوای نیوتن و لایب نیتز
گنجینه ریاضی - انتگرال و دعوای نیوتن و لایب نیتز - علمی، پژوهشی، فرهنگی و انتشاراتی
برنهارد ریمان
دانلود کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry
انالیز ریاضی
در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه
برنهارد ریمان
دانلود رایگان کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry - دانلود رایگان کتب و
برچسب :
انتگرال ریمان