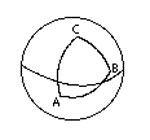
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید.

انواع مثلث

• مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.
• مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.

البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.

• مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.
• مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.
• مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.
• 

300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.
یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود.

محاسبه مساحت مثلث

برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم

روش هندسی

برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم:

 

در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است:

تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل

برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.

روش برداری

محاسبه مساحت متوازی الاضلاع با استفاده از ضرب خارجی دو بردار

مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این مفدار ،اندازه ضرب خارجی دو بردار AB و AC میباشد.پس مساحت مثلث ABC برابر با نصف اندازه ضرب خارجی دو بردار AB و AC خواهد شد.

روش مثلثاتی

استفاده از مثلثات برای پیدا کردن ارتفاع مثلث

ارتفاع یک مثلث را میتوان با استفاده از روابط مثلثاتی بدست آورد.به عنوان مثال در شکل روبرو ارتفاع مثلث از فرمول محاسبه میشود.اگر این فرمول را درفرمول جایگذاری کنیم فرمول بدست می آید:

روش مختصاتی

فرض میکنیم نقطه A به مختصات (0, 0)یک راس از مثلث باشد و نقاط B به مختصات(x1, y1) و C به مختصات(x2, y2) دو راس دیگر مثلث باشند.در این صورت مساحت مثلث نصف مقدار|x1y2 − x2y1| خواهد شد.

فرمول heron

راه دیگر محاسبه مساحت مثلث استفاده از فرمول heron است. این فرمول به صورت زیر است:

منشور: (Prism)

منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکل است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاعها تشکیل شده است.

معرفی منشور 5 پهلو:

نام شکل: منشور 5 پهلو

یال های منشور: 'EE',DD',CC',BB',AA

وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند.

ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است.

قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند.

رابطه های مهم:

ارتفاع × مساحت قاعده = حجم منشور

ارتفاع × محیط قاعده = مساحت جانبی منشور

مساحت دو قاعده + مساحت جانبی = مساحت کل منشور

استوانه: (Cylinder)

نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است.

اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد.

در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است.

رابطه های مهم:

ارتفاع×مساحت قاعده(دایره) = حجم استوانه

ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه

مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه

هرم: (pyramid)

هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند.

معرفی هرم منتظم:

نام شکل: هرم منتظم.

رأس هرم: نقطه S

ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO)

قاعده هرم: پنج ضلعی منتظم ABCDE

سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH).

وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم.

یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA

رابطه های مهم:

مخروط : (cone)

مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است و در اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی نمونه هایی به شکل مخروط هستند.

معرفی مخروط :

نام شکل : مخروط

رأس :نقطه ی s

ارتفاع :پاره خط SO ضلعی که مثلث قائم الزاویه را حول آن دوران داده ایم تا مخروط بوجود آید.

پاره خطی است که از رأس مخروط بر صفحه ی قاعده ی آن عمود است .

قاعده ی مخروط : دایره c به مرکز O و شعاع oB را قاعده ی مخروط می نامیم.

مولد مخروط :پاره خط SA یا SB ، وتر مثلث قائم الزاویه که مخروط را بوجود آورده است.

رابطه های مهم :

کره : (sphere)

کره به معنی گوی و آن چه که به شکل گوی باشد، است و در اصطلاح هندسه شکلی است که از دوران نیم دایره حول قطرش بوجود می آید . مانند توپ ، گوی چوگان

معرفی کره:

مرکز کره :نقطه ی O

شعاع کره :R (فاصله ی نقاط روی سطح کره از مرکز کره)

دایره ی عظیمه :اگر یک کره را نصف کنیم، دایره ای که از نصف کردن کره بدست می آید،

دایره عظیمه نام دارد .

رابطه های مهم :

1- اگر مثلث قائم الزاویه ای را حول وترش دوران دهیم ، دو مخروط پدید می آید که قاعده های آن ها بر هم منطبق اند.

مثال: مثلث قائم الزاویه ای به اضلاع 6 ، 8 ، 10 ، را حول وتر این مثلث دوران می دهیم . حجم جسم حاصل را حساب کنید .

حل:

2- با توجه به دستور محاسبه ی مساحت کره (r۲ ת 4) مشخص می شود که اگر شعاع کره ای را a برابر کنیم مساحت آن a۲ برابر می شود.

مثال: اگر شعاع کره ای را 5 برابر کنیم ، مساحت آن چه تغییری می کند؟

حل:

3- با توجه به دستور محاسبه ی حجم کره مشخص می شود که اگر شعاع کره ای را a برابر کنیم، حجم آن a۲ برابر می شود.

مثال: اگر شعاع کره ای را 3 برابر کنیم ، حجم آن چه تغییری می کند؟

حل:

یعنی حجم کره ی جدید 27 برابر جحم کره ی قدیمی می باشد.

4- اگر مکعبی را در یک کره محاط کنیم ، قطر مکعب با قطر کره مساوی است .

5- از دوران یک ذوزنقه ی قائم الزاویه حول ساق قائم ، مخروط ناقصی پدید می آید که حجم آن ازدستور زیر قابل محاسبه است:

تست1 :

مثلث ABC راحول وتر BC دوران می دهیم. حجم شکل حاصل برابر است با :

(3=ת)

د)2

ج)2

ب)2

الف)

---

‏ تست2 :

اگر شعاع قاعده ی یک مخروط را دو برابر و ارتفاع آن را 3 برابر کنیم ، حجم مخروط چند برابر خواهد شد؟

د) 8 برابر

ج)12 برابر

ب) 6 برابر

الف) 4 برابر

---

‏ تست3 :

اگر شعاع قاعده ی استوانه ای را 3 برابر و ارتفاع آن را ثلث کنیم ، حجم استوانه حاصل .......

د) 9 برابر می شود

ج)تغییر نمی کند

ب)3 برابر می شود

الف) ثلث می شود

---

‏ تست4 :

در کره ای به شعاع یک مکعب محاط شده است . نسبت حجم این کره به مکعب چند است؟

د)

ج)2

ب)2

الف)

---

‏ تست5 :

گسترده ی سطح جانبی یک مخروط دوار نیم دایره است.

زاویه ی مولد این مخروط با ارتفاع آن چند درجه است؟

د) ˚15

ج) ˚60

ب) ˚45

الف) ˚

مطالب مشابه :

توابع مثلثاتی

زرین - توابع مثلثاتی - علمی فرهنگی وسیاسی زرین نسبت های مثلثاتی زوایای 3x :

---

جدول نسبتهای مثلثاتی برای زوایای 0 تا 90 درجه

\\\\ کشکول بشیر //// - جدول نسبتهای مثلثاتی برای زوایای 0 تا 90 درجه - یادداشتهای یک معلم

---

مثلث

مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز روش مثلثاتی .

---

نسبت های مثلثاتی

در ریاضیات دایره مثلثاتی دایره‌ای به شعاع واحد است. x و y دو می‌دانیم که زوایای B و C

---

مثلث

نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث مثلثی را گویند که تمام زوایای داخلی آن کمتر

---

روش محاسبه سطح مثلث و اشکال هندسی

نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث مثلثی را گویند که تمام زوایای داخلی آن کمتر

---

برچسب :
زوایای مثلثاتی