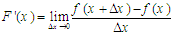قواعد مشتق گیری توابع

هرگاه بخواهیم از تابع f(x) مشتق بگیریم,مشتق این تابع به صورت زیر تعریف می شود:

همچنین برای محاسبه ی مشتق تابع در نقطه ای خاص که شیب خط مماس در آن نقطه می باشد از رابطه ی زیر استفاده می شود.

زاویه ی بین نیم مماس ها نیز از رابطه ی زیر محاسبه می شودکه در آن L1 و L2 مقادیر مشتق چپ و راست نقطه ی مورد نظر می باشند:

نکات مهم مشتق گیری توابع :

در این قسمت از آموزش ریاضیات با نکات مهمی در مشتق گیری آشنا می شوید:

برای مشتق گرفتن از توابع قدر مطلق و جزء صحیح در نقطه ای خاص ابتدا باید علامت قدر مطلق و جزء صحیح را از بین ببریم سپس اقدام به مشتق گیری نماییم.

مشتق عامل صفر:

هرگاه یک تابع به نام f(x) داشته باشیم و مشتق این تابع را از ما بخواهند و f(x)=0 باشد فقط از علملی که صفر شده است مشتق می گیریم و باقی عبارات را عینا می نویسیم.

اگر تابعی پیوستگی راست داشته باشد می تواند مشتق راست داشته باشد(ممکن است مشتق راستی در کار نباشد)

اگر تابعی پیوستگی چپ داشته باشد می تواند مشتق چپ داشته باشد.(اما ممکن است مشتق چپی در کار نباشد)

اگر تابعی فاقد پیوستگی راست و پیوستگی چپ باشد,این تابع مشتق راست و مشتق چپ نیز نخواهد داشت.قبل از گرفتن مشتق راست و مشتق چپ نوع پیوستگی بایستی بررسی شود.

مشتق گیری ازتوابع مثلثاتی وقدرمطلق :

مشتق توابع مثلثاتی:

در این بخش از سری آموزش های مشتق گیری در ریاضیات به مبحث مشتق توابع مثلثاتی و توابع معکوس مثلثاتی و تابع قدر مطلق می پردازیم:

برای محاسبه ی مشتق توابع مثلثاتی از روابط ذیل استفاده می شود:

برای محاسبه ی مشتق توابع معکوس مثلثاتی از روابط زیر استفاده می شود

مشتق گیری از تابع قدر مطلق :

برای محاسبه ی مشتق تابع قدر مطلق می توانید از تابع زیر استفاده نمایید:

در این قسمت از سری آموزش های ریاضیات,به آموزش و نکات مشتق و مشتق گیری می پردازیم:

هنگامی که از شما مشتق تابعی خواسته می شود شما بایستی با استفاده از اطلاعاتی که از قبل در مورد آن تابع و مشتق آن تابع در دست دارید مشتق آن تابع را محاسبه نمایید.گاهی اوقات در برخی روابطی که به شما داده می شود یک یا چند تابع ترکیب شده اند که شما برای محاسبه ی مشتق آن بایستی برخی قواعد مشتق گیری را که در اینجا می آموزید رعایت نمایید.

در عمل مشتق گیری ابتدا کار ضریب و توان را انجام می دهیم.

توضیح:یعنی قبال از هر کاری بهتر است که ابتدا تکلیف مشتق ضریب و توان تابع را مشخص کنید.

مشتق عبارت توان دار از فرمول زیر بدست می آید.

مشتق عبارات کسری از فرمول زیر بدست می آید:

مشتق دو عبارت که در هم ضرب شده اند از فرمول زیر حساب می شود:

مشتق توابع رادیکالی از فرمول ذیل بدست می آید:

فرمول هاي مشتق

تابع $f(x) =\,$	مشتق $f'(x) =\,$	شرايط
$a\,\!$	$0\,\!$	$x\,\in\mathbb{R}$
$a x\,\!$	$a\,\!$	$x\,\in\mathbb{R}$
$1 \over x\,\!$	$- {1 \over x^2}\,\!$	$x\,\in\mathbb{R}^*$
$\sqrt{x}\,\!$	${1 \over 2\sqrt{x}}\,\!$	$x\,\in\mathbb{R}_+^*$
$a x^n\,\!$	$anx^{n-1}\,\!$	$n\,\in \mathbb N^*\quad x\,\in\mathbb{R}$
$a x^n\,\!$	$anx^{n-1}\,\!$	$n\,\in \mathbb Z \setminus\mathbb N\quad x\,\in\mathbb{R}^*$
$a x^c\,\!$	$acx^{c-1}\,\!$	$c\,\in \mathbb R \setminus\mathbb Z\quad x\,\in\mathbb{R}^{*+}$
$\cos(x)\,\!$	$-\sin(x)\,\!$	$x\,\in\mathbb{R}$
$\sin(x)\,\!$	$\cos(x)\,\!$	$x\,\in\mathbb{R}$
$\tan(x)\,\!$	$1 \over \cos^2(x)$ ou $1+\tan^2(x)\,\!$	$x\neq {\pi \over 2} + k\pi$ , $k \in \mathbb{Z}$
$a^x\,\!$	$a^x \ln a\,\!$	$a\,\in\mathbb{R}_+^* \quad x\,\in\mathbb{R}$
$\ln \|x\|\,\!$	$1 \over x\,\!$	$x\,\in\mathbb{R}^*$
$\exp{x}\,\!$	$\exp{x}\,\!$	$x\,\in\mathbb{R}$