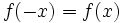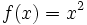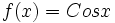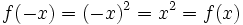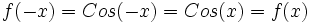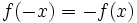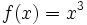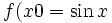آموزش ریاضی/انواع تابع
|
دید کلی
مقادیر یک کمیت متغیر غالبا به مقادیر کمیت متغیر دیگری بستگی دارد مثلا: فشار در دیگ بخار نیروگاه به دمای بخار بستگی دارد. آهنگ تخلیه آب از وان حمام ، وقتی در پوش وان را بر میداریم به ارتفاع آب وان بستگی دارد. مساحت دایره به شعاع بستگی دارد. در هر یک از این مثالها مقادیر یک کمیت متغیر مثل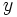 وابسته به مقدار کمیت متغیر دیگری است که میتوانیم آن را
وابسته به مقدار کمیت متغیر دیگری است که میتوانیم آن را  بنامیم و چون در هر مورد مقدار
بنامیم و چون در هر مورد مقدار 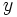 توسط مقدار
توسط مقدار  کاملا معین میشود میگوئیم
کاملا معین میشود میگوئیم 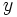 تابعی از
تابعی از  است.
است. تعریف
هر تابع از مجموعهای چون به مجموعهای چون
به مجموعهای چون  ، قاعدهای است که به هر عنصر
، قاعدهای است که به هر عنصر  ، تک عنصری از
، تک عنصری از  را منسوب میکند.
را منسوب میکند. بررسی از روی شکل هندسی
اگر بخواهیم به طور هندسی نموداری را بررسی میکنیم، آیا نمودار تابع هست یا نیست. به این ترتیب عمل میکنیم که به ازای هر خط موازی محور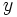 ها نمودار مورد نظر حداکثر در یک نقطه با خط رسم شده نقطه تلاقی داشته باشد یا به عبارت دیگر نموداری ، شکل تابع است که به ازای
ها نمودار مورد نظر حداکثر در یک نقطه با خط رسم شده نقطه تلاقی داشته باشد یا به عبارت دیگر نموداری ، شکل تابع است که به ازای  های یکسان ،
های یکسان ، 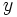 های متفاوت نداشته باشد. مثلا تابع
های متفاوت نداشته باشد. مثلا تابع  را در نظر میگیریم که به ازای
را در نظر میگیریم که به ازای  های متفاوت (
های متفاوت ( ) یک
) یک 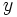 دارد ولی نمودار
دارد ولی نمودار  به ازای
به ازای  های یکسان ،
های یکسان ، 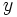 های متفاوتی دارد، بنابراین
های متفاوتی دارد، بنابراین  نمیتواند تابع باشد.
نمیتواند تابع باشد.
|
ساختمان یک تابع
توابع را از جهات مختلفی میتوان مورد بررسی قرار دارد، مثلا میتوان زوج یا فرد بودن ، جبری یا مثلثاتی بودن – متناوب یا نامتناوب بودن ، پیوسته یا ناپیوسته بودن و بسیاری از موارد دیگر که در این مجال نمیگنجد وجود دارد که میشود راجع به آنها در مورد توابع بحث نمود در این مقاله به تعدادی از این بحثها به اجمال خواهیم پرداخت:توابع زوج و فرد
- برای شناسایی یک تابع زوج از روی نمودار میتوان گفت توابع زوج نسبت به محور
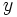 ها متقارن هستند. و از روی خاصیت جبری میشود این گونه توصیف کرد که اگر
ها متقارن هستند. و از روی خاصیت جبری میشود این گونه توصیف کرد که اگر 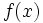 را یک تابع زوج در نظر بگیریم برای آن به ازای هر
را یک تابع زوج در نظر بگیریم برای آن به ازای هر  که عنصر دامنه
که عنصر دامنه 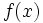 باشد:
باشد: 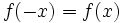 مثل توابع
مثل توابع 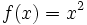 و
و 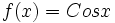 که برای آنها
که برای آنها 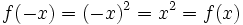 و
و 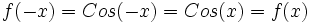 .
.
- برای شناسایی تابع فرد از روی نمودار میتوان گفت توابع فرد نسبت به که مبدأ مختصات متقارن هستند. در مورد خواص جبری ، برای توابع فرد این خاصیت جبری حاکم است که
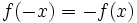 و
و 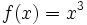 یا
یا 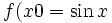 که در آنها داریم:
که در آنها داریم:


- نکته: نمودار معادلاتی که صرفا شامل توانهای زوج
 باشد و نسبت به محور
باشد و نسبت به محور 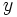 ها متقارن هستند را توابع زوج میگوئیم، اما قاعده متناظری برای توان فرد وجود ندارد.
ها متقارن هستند را توابع زوج میگوئیم، اما قاعده متناظری برای توان فرد وجود ندارد.
توابع متناوب
تابع را متناوب گوییم هرگاه برای هر عضو دامنه آن مقداری ثابت و حقیقی مانند
را متناوب گوییم هرگاه برای هر عضو دامنه آن مقداری ثابت و حقیقی مانند  یافت شود؛ به قسمی که اولا
یافت شود؛ به قسمی که اولا  عضو آن دامنه و ثانیا
عضو آن دامنه و ثانیا  باشد.
باشد.  را یک دوره تناوب تابع
را یک دوره تناوب تابع 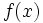 میگوئیم. به سادگی میتوان دریافت که دوره تناوب یک تابع متناوب منحصر به فرد نیست. برای مثال تابع
میگوئیم. به سادگی میتوان دریافت که دوره تناوب یک تابع متناوب منحصر به فرد نیست. برای مثال تابع  که
که  تعریف شده است همه با دوره تناوب
تعریف شده است همه با دوره تناوب  متناوب است هم با دوره تناوب
متناوب است هم با دوره تناوب  ، زیرا:
، زیرا:
خاصیت هندسی توابع متناوب
با توجه به تساوی نتیجه میگیریم که نمودار تابع متناوب در صورت جابجایی به یک بردار انتقال به اندازه
نتیجه میگیریم که نمودار تابع متناوب در صورت جابجایی به یک بردار انتقال به اندازه  در هر جهت تغییر نمیکند.
در هر جهت تغییر نمیکند. یک به یک و پوشا بودن یک تابع
به طور کلی تابعی چون را یک به یک گوئیم هرگاه به ازای هر عضوی از دامنه فقط و فقط یک عضو منحصر به فرد از برد ، جواب تابع باشد. و اگر بخواهیم از روی شکل تشخیص بدهیم، به ازای هر خط موازی محور
را یک به یک گوئیم هرگاه به ازای هر عضوی از دامنه فقط و فقط یک عضو منحصر به فرد از برد ، جواب تابع باشد. و اگر بخواهیم از روی شکل تشخیص بدهیم، به ازای هر خط موازی محور  ها ، خط زرسم شده نمودار را حداکثر در یک نقطه قطع کند. مثل نمودار
ها ، خط زرسم شده نمودار را حداکثر در یک نقطه قطع کند. مثل نمودار  .
. تعریف پوشا بودن
تابعی مثل را روی دامنهاش پوشا میگوئیم هرگاه به ازای هر عضو از دامنه جوابی از برد موجود باشد. و برای تشخیص از روی نمودار ، به ازای هر خط موازی محصور
را روی دامنهاش پوشا میگوئیم هرگاه به ازای هر عضو از دامنه جوابی از برد موجود باشد. و برای تشخیص از روی نمودار ، به ازای هر خط موازی محصور  ها ، تابع حداقل در یک نقطه قطع شود. البته دقت میکنیم که به ازای دو خط رسم شده باید خاصیت فوق ، برقرار باشد.
ها ، تابع حداقل در یک نقطه قطع شود. البته دقت میکنیم که به ازای دو خط رسم شده باید خاصیت فوق ، برقرار باشد. تابع قدر مطلق
قدر مطلق عددی مانند ، عدد
، عدد  است. اگر
است. اگر  مثبت باشد، قدر مطلق آن همان
مثبت باشد، قدر مطلق آن همان  است ، ولی اگر
است ، ولی اگر  منفی باشد، قدر مطلق آن
منفی باشد، قدر مطلق آن  است. اگر
است. اگر  صفر باشد ، قدر مطلقش صفر است. نماد قدر مطلق
صفر باشد ، قدر مطلقش صفر است. نماد قدر مطلق  به صورت
به صورت  است. اگر دقت کنید تابع قدر مطلق متشکل از خطوط
است. اگر دقت کنید تابع قدر مطلق متشکل از خطوط  و
و  که به ترتیب برای
که به ترتیب برای  و
و  انتخاب شده است، یعنی از خط
انتخاب شده است، یعنی از خط  قسمتی که
قسمتی که  های آن مثبت هستند و از خط
های آن مثبت هستند و از خط  قسمتهایی که
قسمتهایی که  های آن منفی هستند را انتخاب میکند.
های آن منفی هستند را انتخاب میکند. تابع بزرگترین عدد صحیح یا جزء صحیح
بزرگترین عدد صحیحی که نابیشتر از عددی چون باشد، بزرگترین عدد صحیح موجود در
باشد، بزرگترین عدد صحیح موجود در  نامیده میشود نماد آن
نامیده میشود نماد آن  است. تابعی مثل
است. تابعی مثل  دارای دامنه
دارای دامنه  و برد اعداد صحیح است. تابع جز صحیح یک تابع پلهای است. مدل بسیاری از چیزهایی که در اطراف خود میبینیم میتوانیم به صورت پلهای در نظر گرفت، مثلا هزینه پست کردن بسته به صورت تابعی از وزن ، عملکرد چراغ چشمک زن به صورت تابعی از زمان ، تابع پلهای دارای نقاط ناپیوستگی هستند، یعنی که در آنها تابع از مقداری به مقدار دیگر میجهد بدون اینکه هیچ یک از مقادیر میانی را انتخاب کند.
و برد اعداد صحیح است. تابع جز صحیح یک تابع پلهای است. مدل بسیاری از چیزهایی که در اطراف خود میبینیم میتوانیم به صورت پلهای در نظر گرفت، مثلا هزینه پست کردن بسته به صورت تابعی از وزن ، عملکرد چراغ چشمک زن به صورت تابعی از زمان ، تابع پلهای دارای نقاط ناپیوستگی هستند، یعنی که در آنها تابع از مقداری به مقدار دیگر میجهد بدون اینکه هیچ یک از مقادیر میانی را انتخاب کند. تابع همانی
تابع همانی تابعی است که به هر عدد همان عدد را نسبت میدهد. یکی از کاربردهای تابع همانی ، آزمون توابع معکوس میباشد. به این ترتیب که اگر معکوس
معکوس  باشد ترکیب آنها تابع همانی خواهد بود.
باشد ترکیب آنها تابع همانی خواهد بود. توابع مثلثاتی
بسیاری از پدیدههای طبیعی متناوب هستند؛ به این معنا که بعد از دوره معینی از زمان تکرار میشوند. چنین پدیدههایی را میتوان به آسانی با توابع سینوسی و کسینوسی بررسی کرد. اگر توابع با آرایش یافته باشد به این دسته از توابع ، توابع مثلثاتی خواهیم گفت. یکی از خاصیتهای توابع مثلثاتی تناوبی بودن آنهاست؛ زیرا مثلا به ازای هر زاویه
آرایش یافته باشد به این دسته از توابع ، توابع مثلثاتی خواهیم گفت. یکی از خاصیتهای توابع مثلثاتی تناوبی بودن آنهاست؛ زیرا مثلا به ازای هر زاویه  داریم:
داریم:

توابع چند جملهای
جملهای منفرد به صورت را که در آن
را که در آن  ثابت دلخواه و
ثابت دلخواه و  عدد صحیح نامنفی است، یک تک جملهای بر حسب
عدد صحیح نامنفی است، یک تک جملهای بر حسب  مینامند. مجموع تعدادی متناهی تک جملهای بر حسب
مینامند. مجموع تعدادی متناهی تک جملهای بر حسب  یک چند جملهای
یک چند جملهای  نام دارد.
نام دارد. توابع متعالی
امروزه ، تابعی چون را متعالی مینامند اگر در معادله به صورت:
را متعالی مینامند اگر در معادله به صورت:
که در آن ضرایب:
 ،
،  و ... و
و ... و  چند جملهایهایی بر حسب
چند جملهایهایی بر حسب  هستند ، صدق نکند. تابعی مثل
هستند ، صدق نکند. تابعی مثل  که یکی از جوابهای
که یکی از جوابهای  است
است  ، یکی از توابع موسوم به توابع متعالی است. نام "متعالی" را اویلر برای توصیف اعدادی انتخاب کرد که ریشه یک معادله چند جملهای نیستند. اویلر میگوید که این اعداد متعالی از آنهایی هستند که روشهای جبری در موردشان کارساز باشد".
، یکی از توابع موسوم به توابع متعالی است. نام "متعالی" را اویلر برای توصیف اعدادی انتخاب کرد که ریشه یک معادله چند جملهای نیستند. اویلر میگوید که این اعداد متعالی از آنهایی هستند که روشهای جبری در موردشان کارساز باشد".
مطالب مشابه :
معرفی تابع قدر مطلق و خواص آن
در ریاضیات، قدر مطلق (Absolute Value) عددی حقیقی، مقدار عددی آن بدون در نظر گرفتن علامتش است.
ریاشی
تابع قدر مطلق و خواص قدر مطلق.
جلسه ی دوم (اعداد حقیقی - قدر مطلق - بازه ها)
ریاضیات مقدماتی و تخصصی - جلسه ی دوم (اعداد حقیقی - قدر مطلق - بازه ها) - مهدی مفیدی احمدی
فضیلت و خواص سوره قدر
سلوک عرفای اسلامی - فضیلت و خواص سوره قدر وب سایت حجت الاسلام سید عباس موسوی مطلق.
دنباله و همگرایی
بوضوح n ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز همچنین بنا به خواص قدر مطلق
توپولوژی با طعم ریاضیات ...
اين اعمال با خواص معين، R را به عنوان گروه، حلقه و (به عنوان نمونه R با متر قدر مطلق يعني| d
انواع تابع
در مورد خواص جبری ، برای توابع فرد این خاصیت جبری حاکم قدر مطلق عددی مانند x، عدد است.
دنباله وهمگراي
بوضوح n ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز همچنین بنا به خواص قدر مطلق
آموزش ریاضی/انواع تابع
در مورد خواص جبری ، برای توابع فرد این خاصیت جبری حاکم است که و یا که در آنها تابع قدر مطلق
دانلود جزوه کامل ریاضی رشته تجربی
مشتق تابع قدر مطلقی اکسترمم های مطلق خواص مشترک اکسترمم نسبی و عطف
برچسب :
خواص قدر مطلق