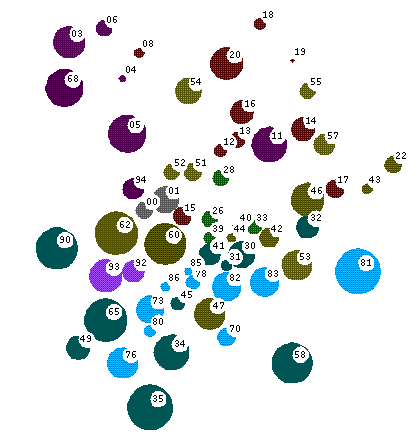اطلس ریاضی: کاربردهای ریاضیات در علوم

اطلس ریاضی:

کاربردهای ریاضیات در علوم

ترجمه: ابوالفضل گروئی - منبع: سایتwww.math.niu.edu

* در صورت تمایل میتوانید اصل مقاله را در انتها مطالعه فرمائید.

از نظر تاریخی، این نیازهای علوم فیزیکی بوده است که محرک توسعه بسیاری از قسمتهای ریاضیات، به ویژه آنالیز بوده اند. گاهی اوقات مشکل است که کاربردها را از نظر ریاضی طبقه بندی کرد، چرا که ابزارهائی از چند حوزه ریاضیات ممکن است به کار گرفته شده باشند. ما روی این کاربردها نه فقط با بحث درباره طبیعت نظم (و سازماندهی) آنها متمرکز میشویم، بلکه برهمکنش آنها با ریاضیات را نیز مد نظر قرار میدهیم.

بیشتر حوزه ها در این گروه (نقاط آبی در تصویر) در مجموع با عنوان «فیزیک ریاضی» شناخته شده اند. تا اندازه ای، ابزارهای ریاضی جدیدتر و به طور پیشرونده پیچیده تر در مهندسی، زیست شناسی و علوم اجتماعی (نواحی بنفش در تصویر) به کار گرفته میشوند.

70- مکانیک ذرات و سیستمها: مطالعه دینامیک مجموعه های ذرات یا توده های جامد (تو پر)، شامل توده های چرخان یا لرزان. از اصول تغییرات (انرژی-کمینه سازی) همچنین معادلات دیفرانسیل استفاده میکند.

Equilibrium in statistical mechanics: systems exchanging energy are most likely to have individual energies that maximize the overall number of states. (Image by Prof. Mehran Kardar.)

تعادل در مکانیک آماری: سیستمهای مبادله کننده انرژی تمایل به داشتن انرژیهای مشخصی دارند که تعداد کل حالتها را بیشینه میکند (تصویر از پروفسور مهران کاردار از سایت: www.core.org.cn)

74- مکانیک توده های تغییر شکل پذیر: معادلات الاستیسیته و پلاستیسیته، انتشار موج، مهندسی و حوزه هائی در جامدات ویژه مانند خاکها و بلورها را در نظر میگیرد.

مثالهای تغییر شکل کره: الف) شکل ابتدائی ب) کشش و پ) نیشگون گیری.

76- مکانیک سیالات: هوا، آب و دیگر سیالات در حال حرکت را بررسی میکند؛ همچنین: تراکم، اغتشاش، نفوذ، انتشار موج و غیره. از نظر ریاضی، مطالعه حلهای معادلات دیفرانسیل شامل روشهای عددی در مقیاس بالا (برای نمونه، روش اجزای محدود) را در بر میگیرد.

Image by Bomphrey et al. (Phy. of Fluid 2002)

بررسی رفتار سیال (هوا) در اطراف یک ملخ چرخان.

تصویر از بامفری و همکاران (در مجله فیزیک سیال ۲۰۰۲).

78- نورشناخت (اپتیک)، تئوری الکترومغناطیس: بررسی انتشار و تغییر شکل امواج الکترومغناطیسی شامل مباحث تداخل و پراش است. در کنار شاخه های متداول آنالیز، این حوزه مباحث هندسی مانند مسیرهای پرتوهای نوری را نیز در بر میگیرد.

انتهای رشته(فیبر)های نوری.

80- ترمودینامیک کلاسیک، انتقال گرما: بررسی شارش گرما از میان ماده شامل تغییر فاز و احتراق است. از نظر تاریخی منشاء سریهای «فوریه» است.

نیمرخ (پروفایل) توزیع دما در لوله آب خنک کننده.

81- نظریه کوانتوم: حلهای معادله (دیفرانسیلی) شرودینگر را بررسی میکند. همچنین، شامل مباحثی از نظریه گروه Lie و نظریه گروه کوانتومی، نظریه توزیعها و مباحثی از آنالیز تابعی، مسائل یانگ-میلز، نمودارهای فاینمن و غیره میباشد.

جهان کوانتومی.

A schematic, called a Feynman diagram, of two virtual gluons from colliding LHC protons interacting to produce a hypothetical Higgs boson, a top quark, and an antitop quark.

یکی از نمودارهای فاینمن که دو گلوئون مجازی به وجود آمده از برخورد پروتونهای LHC را نشان میدهد که برای تشکیل یک بوزون هیگز فرضی، یک کوآرک بالا و یک کوآرک پائین با هم برهمکنش میدهند.

82- مکانیک آماری، ساختار ماده: بررسی سیستمهای ذرات در مقیاس بزرگ، شامل سیستمهای تصادفی و سیستمهای متحرک یا استنتاجی است. انواع ویژه ای از مواد شامل سیالات، بلورها، فلزات و دیگر جامدات بررسی میشوند.

تئوریهای سرعتهای واکنش، کینتیک، انتقال جرم و شیمی فیزیک همگی از مکانیک آماری استفاده میکنند.

83- نظریه نسبیت و گرانش: هندسه دیفرانسیلی، آنالیز و نظریه گروه است که در فیزیک و در مقیاس بزرگ یا در مکانهای بسیار دور (یعنی سیاهچاله ها و کیهان شناسی) به کار گرفته میشوند.

آلبرت اینشتین، پایه گذار نظریه نسبیت.

85- اختر شناسی و اختر فیزیک: مانند مکانیک آسمانی (سماوی)، از نظر ریاضی بخشی از مکانیک ذرات است (!). کاربردهای اصلی در این حوزه به ساختار، تکامل و برهمکنش ستارگان و کهکشانها مربوط میشوند.

تصویر ترکیبی از کهکشان M81. از: NASA/JPL-Caltech

86- زمین فیزیک (ژئوفیزیک): کاربردها نوعا ماده در مکانیک و مکانیک سیالات را همانند بالا در بر میگیرند، اما برای مسائل در مقیاس بزرگ (این موضوع یک جامد بسیار بزرگ و استخر بزرگی از سیال را در نظر میگیرد!).

93- نظریه سیستمها، کنترل: تغییر در طول زمان سیستمهای پیچیده را بررسی میکند؛ مانند سیستمهائی که در مهندسی وجود دارند. به ویژه، میتواند برای شناخت سیستم-تعیین معادلات یا مشخصه هائی که بر توسعه آن حاکمند- یا برای کنترل سیستم–برای انتخاب مشخصه ها (یعنی از طریق حلقه های بازخورد)- برای رسیدن به یک حالت مطلوب امتحان شود. از موارد ویژه میتوان به موضوعاتی در پایداری (آرایشهای حالت پایدار) و اثرات تغییرات تصادفی و نویز (سیستمهای تصادفی) اشاره کرد. تا زمانیکه قلمرو «فرمان شناسی (سیبرنتیک)» یا «رباتیک» محبوبند، شاید بتوان این را در عمل میدانی از کاربرد معادلات دیفرانسیل (یا تفاضلی) آنالیز تابعی، آنالیز عددی و آنالیز جهانی (یا هندسه دیفرانسیل) به شمار آورد.

92- زیست شناسی و دیگر علوم طبیعی: وابستگیهائی که شایسته عنوان وابستگی آشکار هستند شامل شیمی، زیست شناسی، زنتیک و پزشکی هستند. واضح است که در شیمی و بیوشیمی نظریه گراف، هندسه دیفرانسیل و معادلات دیفرانسیل نقش ایفاء میکنند. فناوری پزشکی از تکنیکهای انتقال و به نمایش درآوردن اطلاعات بهره میبرد. زیست شناسی (شامل دانش رده بندی «تاکسونومی» و زیست-باستانشناسی) از استنتاج آماری و دیگر ابزارها استفاده میکنند.

91- نظریه بازی، اقتصاد، علوم اجنماعی و رفتاری: شامل روانشناسی، جامعه شناسی و دیگر علوم اجتماعی به عنوان یک گروه است. بیشتر علوم رفتاری (شامل زبانشناسی!) آمیخته ای از تکنیکهای آماری شامل طراحی تجربی و دیگر مباحث ترکیبی را مورد استفاده قرار میدهند. اقتصاد و دارائی نیز از ابزارهای آماری به خصوص آنالیز سریهای زمانی استفاده میکنند. چند مبحث مانند نظریه رأی دهی بیشتر ترکیبی هستند. این طبقه بندی نیز شامل نظریه بازی است که در واقع اصلا درباره بازیها نیست بلکه درباره بهینه سازی است که ترکیب راهبردهائی را در نظر میگیرد که به یک خروجی بهینه منجر شود (ناحیه 91 در نقشه ریاضی نشان داده نشده است؛ این ناحیه در سال 2000 از قسمتهائی از بخشهای 90 و 92 به وجود آمد).

مشاهده میکنید که شاخه های ریاضیات خیلی به حوزه های فیزیک ریاضی و بخشهائی از آنالیز، به خصوص آن بخشهائی که به معادلات دیفرانسیل مربوطند، پیوستگی دارند. علوم دیگر به اینها و همچنین احتمال و آمار و به طور فزاینده، روشهای عددی متصل میشوند.

***

در زیر میتوانید اصل مقاله را به زبان انگلیسی مشاهده فرمائید:

Historically, it has been the needs of the physical sciences which have driven the development of many parts of mathematics, particularly analysis. The applications are sometimes difficult to classify mathematically, since tools from several areas of mathematics may be applied. We focus on these applications not by discussing the nature of their discipline but rather their interaction with mathematics.

Most of the areas in this group (the blue ones in the picture here) are collectively known as "mathematical physics". Somewhat more recently, increasingly sophisticated mathematical tools are used in the engineering, biology, and the social sciences (the violet areas in the picture).

70: Mechanics of particles and systems studies dynamics of sets of particles or solid bodies, including rotating and vibrating bodies. Uses variational principles (energy-minimization) as well as differential equations.

74: Mechanics of deformable solids considers questions of elasticity and plasticity, wave propagation, engineering, and topics in specific solids such as soils and crystals.
76: Fluid mechanics studies air, water, and other fluids in motion: compression, turbulence, diffusion, wave propagation, and so on. Mathematically this includes study of solutions of differential equations, including large-scale numerical methods (e.g the finite-element method).
78: Optics, electromagnetic theory is the study of the propagation and evolution of electromagnetic waves, including topics of interference and diffraction. Besides the usual branches of analysis, this area includes geometric topics such as the paths of light rays.
80: Classical thermodynamics, heat transfer is the study of the flow of heat through matter, including phase change and combustion. Historically, the source of Fourier series.
81: Quantum Theory studies the solutions of the Schrödinger (differential) equation. Also includes a good deal of Lie group theory and quantum group theory, theory of distributions and topics from Functional analysis, Yang-Mills problems, Feynman diagrams, and so on.
82: Statistical mechanics, structure of matter is the study of large-scale systems of particles, including stochastic systems and moving or evolving systems. Specific types of matter studied include fluids, crystals, metals, and other solids.
83: Relativity and gravitational theory is differential geometry, analysis, and group theory applied to physics on a grand scale or in extreme situations (e.g. black holes and cosmology).

85: Astronomy and astrophysics: as celestial mechanics is, mathematically, part of Mechanics of Particles (!), the principal applications in this area appear to be concerning the structure, evolution, and interaction of stars and galaxies.
86: Geophysics applications typically involve material in Mechanics and Fluid mechanics, as above, but for large-scale problems (this subject deals with a very big solid and a large pool of fluid!)
93: Systems theory; control study the evolution over time of complex systems such as those in engineering. In particular, one may try to identify the system -- to determine the equations or parameters which govern its development -- or to control the system -- to select the parameters (e.g. via feedback loops) to achieve a desired state. Of particular interest are issues in stability (steady-state configurations) and the effects of random changes and noise (stochastic systems). While popularly the domain of "cybernetics" or "robotics", perhaps, this is in practice a field of application of differential (or difference) equations, functional analysis, numerical analysis, and global analysis (or differential geometry).
92: Biology and other natural sciences whose connections merit explicit connection in the MSC scheme include Chemistry, Biology, Genetics, and Medicine, In chemistry and biochemistry, it is clear that graph theory, differential geometry, and differential equations play a role. Medical technology uses techniques of information transfer and visualization. Biology (including taxonomy and archaeobiology) use statistical inference and other tools.

91: Game theory, economics, social and behavioral sciences including Psychology, Sociology, and other social sciences as a group. The more behavioural sciences (including Linguistics!) use a medley of statistical techniques, including experimental design and other rather combinatorial topics. Economics and finance also make use of statistical tools, especially time-series analysis; some topics, such as voting theory, are more combinatorial. This category also includes game theory, which is actually not about games at all but rather about optimization; which combination of strategies leads to an optimal outcome. [Area 91 is not shown on the MathMap; it was created in 2000 from parts of sections 90 and 92.]

Observe that the branches of mathematics most closely allied with the fields of mathematical physics are the parts of analysis, particularly those parts related to differential equations. The other sciences draw on these as well as probability and statistics and, increasingly, numerical methods.

اطلس ریاضی: کاربردهای ریاضیات در علوم

مطالب مشابه :

کاربرد ریاضی در زندگی

کاربرد ریاضی

معادلات دیفرانسیل

کاربرد ریاضی در زندگی بشر ( 1 )

کاربرد ریاضی در زندگی بشر (۲)

کاربرد لگاریتم در زندگی

کاربرد جبر در کوانتوم

اطلس ریاضی: کاربردهای ریاضیات در علوم

دانلود کتاب معادلات دیفرانسیل بویس