مهارت فرضیه‌سازی

     همان‌طور که در مهارت‌های محاسبات عددی و عملیات ذهنی و تخمین و تقریب عددی بیان شد، روش‌ها و راهبردهای محاسباتی و تخمین‌زدن باید توسط دانش‌آموز توضیح داده شوند. بنابراین روش‌های محاسباتی می‌توانند فرضیاتی باشند که دانش‌آموز می‌سازد و با مثال‌های دیگر می‌توان درستی فرضیه‌های او را بررسی کرد.

     برای مثال، در تقسیم دو کسر فرضیه(روش محاسبه) یک دانش آموز چنین بوده است که صورت‌ها را برهم و مخرج‌ها را بر هم تقسیم کند. این فرضیه را می‌توانیم به صورت زیر بررسی کنیم:

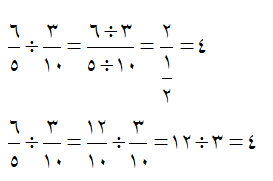
  با این مثال می‌توان گفت، فرضیة بیان شده احتمالاً درست است. با چند مثال دیگر می‌توانیم این روش محاسبه را دقیق بررسی کنیم.

   یکی از اجزای مهم فرضیه‌سازی، تعمیمی یا توسعة فرضیات تعیین شده است. برای مثال، با تجربه چهارضلعی‌های متفاوت، می‌توان این فرضیه را تأیید کرد که مجموع زاویه‌های خارجی هر چهار ضلعی 360 است. این فرضیه را می‌توان دربارة هر n ضلعی تعمیم داد. برای این کار می‌توان پنج‌ضلعی، شش ضلعی و ... را تجربه کرد و یک فرضیه کلی‌تر ساخت: «مجموع زاویه‌های خارجی هر nضلعی 360 است.»

    بحث در مورد تعمیم‌پذیری یک موضوع از گفت‌وگوهای جالب کلاس درس است که بینش دانش‌آموز را در مباحث ریاضی توسعه می‌دهد.

    گاهی فرضیه‌های متفاوت با هم در ارتباط هستند. کشف ارتباط‌های درونی بین فرضیه‌ها از گام‌های مهم و در سطح بالای مهارت‌ فرضیه‌سازی است. بنابراین نمی‌توان از همة دانش‌آموزان انتظار داشت، رابطه‌ها را کشف کنند و تشخیص دهند.

    در روش‌های محاسباتی می‌توان بین فرضیه‌های گوناگون ارتباط برقرار کرد. برای مثال در همان تقسیم کسر، می‌توان بین فرضیة «تقسیم کردن صورت‌ها برهم و مخرج‌ها برهم»، و فرضیة «ضرب کردن در معکوس کسر دوم» ارتباط برقرار کرد. در واقع هر دو فرضیه مفهوم تقسیم کسر با مخرج‌های مساوی برمی‌گردند.

    همان‌طور که گفتیم، پس از بیان هر فرضیه، آن را آزمون می‌کنیم. اصلاح فرضیه‌ها و نظریه‌ها براساس آزمون کردن آن‌ها نیز از اجزای این مهارت است. همچنین می‌توان با آزمون یا تجربه، نقاط ضعف و قوت و یا دامنة درستی یک فرضیه یا نظریه را بررسی کرد. برای مثال، دانش‌آموزی پس از رسم ارتفاع‌های یک مثلث، این فرضیه را ساخته است: «محل برخورد سه ارتفاع یک مثلث، نقطه‌ای داخل آن است.» او پس از این که این فرضیه را آزمون کرد، مشاهده کرد، در یک حالت که مثلث یک زاویة باز داشت، محل برخورد ارتفاع‌ها در خارج مثلث واقع شد. بنابراین فرضیة خود را به این ترتیب اصلاح کرد: «محل برخورد سه ارتفاع یک مثلث که زاویة باز نداشته باشد، داخل مثلث قرار می‌گیرد.»

آیا این فرضیه جدید کامل است؟ در مورد مثلث قائم الزاویه محل برخورد ارتفاع‌های مثلث‌ها کجا واقع می‌شود؟

این مهارت در درس‌های مربوط به هندسه و روابط بین ضلع‌ها، زاویه‌ها و سایر اجزای شکل‌های هندسی مثل مثلث، چهارضلعی‌ها و ... کاربرد بسیار دارد. برای مثال در درس چهارضلعی‌های کلاس چهار دبستان، تمام خاصیت‌های شکل‌های هندسی را می‌توان با استفاده از این مهارت نتیجه‌گیری کرد. به عبارت دیگرف می‌توان فعالیت‌هایی را طرح کرد که دانش‌آموزان بتوانند پس از تجربه روابط بین اجزا را نتیجه‌گیری کنند و برای آن‌ها فرضیه بسازند.

     برای مثال می‌توان چند متوازی الاضلاع رسم کرد و دانش‌آموزان با اندازه‌گیری ضلع‌ها فرضیه‌سازی کنند: «در هر متوازی الاضلاع، ضلع‌های مقابل با هم مساوی هستند.

منبع:clase6.blogfa.com