تانسورها

هر تانسور از مرتبه ی n در فضایی m- بعدی، ساختاری ریاضیاتی است که n شاخص و 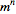مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.

هر شاخص تانسور، فقط مقادیری در محدوده ی تعداد بعدهای فضای تعریفی اختیار می کند. با این حال دخالت ابعاد فضایی تا حدود زیادی در معادلات تانسوری نامربوط به نظر می رسد. تانسورها نوع عمومی تر اسکالرها ( که فاقد شاخص هستند) ،بردارها (که تنها دارای یک شاخص اند) و نیز متریک ها (که فقط دو شاخص دارند) می باشند که می توانند تعداد دلخواه شاخص اختیار کنند.

تانسورها بستر ریاضی مناسب و ساده ای را جهت فرمولبندی و حل مسائل متعدد در سیطره ی مباحث گوناگون فیزیک نظیر مکانیک سیالات و نسبیت عام فراهم می کنند.

نمادگذاری هر تانسور عیناْ شبیه به یک ماتریس است، (مثل )، به جز اینکه یک تانسور مثلا ، ، قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی ،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط" ، تلفیقی از شاخص بالا یا "پادوردا (contravariant)" و شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور متمایز از شکل است.

هنگامی که تانسور نسبت به تفاوت شاخص های پادوردا و هم وردا حساس باشد، تانسور حاصل از نوع عمومی خواهد بود. (در بحث ماتریس ها، یک ماتریس عمومی از جمع دو ماتریس پادمتقارن و متقارن به وجود می آمد که در اینجا نیز همین حالت برای تانسورها برقرار است). عدم تفاوت میان شاخص های هم وردا و پادوردا بیشتر در تانسورهای موردبحث در فضای اقلیدسی مانند تانسورهای دکارتی (Cartesian tensors) مطرح است.

تانسورهای تبدیل شونده از مرتبه ی صفر، اسکالر (scalars) نامیده می شوند که همانند تانسورهای مرتبه ی ۱ یعنی بردارها (vectors) تبدیل می شوند. در نمادنویسی تانسوری، هر بردار به شکل نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم می نویسیم.

می توان عملیات جبری و دیفرانسیل را بر روی تانسورها انجام داد (مانند تانسورهای متریک (metric tensors) و تانسور جایگشت (permutation tensor) یا نماد دلتای کرونکر) که قابلیت تعریف پذیری عملگرهای تانسوری را دارا هستند. [مانند مشتق هم وردا (semicolon derivatives)]. با جابجایی شاخص های هم وردا و پادوردا می توان به عبارات و تانسورهای ساده تری دست یافت که این کار شامل بالابردن (index raising) یا پایین آوردن شاخص ها (index lowering) یا به عبارت کلی بالانس شاخص ها ( index gymnastics) می باشد که آن ها را می توان با ضرب در تانسور متریک، ، ، و ... به دست آورد.

بالانس شاخص ها در دو حالت هم وردا و پادوردا به کمک تانسور متریک:

(Arfken 1985, p. 159).

نمادنویسی تانسوری می تواند یک راه موجز و کوتاه را جهت نوشتن بردارها و اتحادهای عمومی دیگر فراهم کند. به عنوان مثال، در نمادنویسی تانسوری، حاصلضرب نقطه ای (dot product) به واسطه رابطه ی زیر بسیار خلاصه می گردد

که در اینجا برای ساده شدن عبارت تحت جمع زنی نسبت به همه ی شاخص ها، قرارداد جمع اینیشتین را بکار برده ایم. به طور مشابه، می توانیم حاصلضرب خارجی (cross product) را به صورتی مختصر بدین گونه بنویسیم

که تانسور لوی - سیویتا یا تانسور جایگشت (permutation tensor) می باشد.

تانسورهای پادوردای (Contravariant) مرتبه ی دوم، ساختارهای ریاضیاتی هستند که به شکل زیر تبدیل می شوند

به همین شکل تانسورهای هم وردای (Covariant) نیز به صورت زیر تبدیل می شوند

تانسورهای موسوم به مختلط ـ شاخص (Mixed) از مرتبه دو نیز به شکل زیر تبدیل می یابند

چنانچه دو تانسور A و B و هر دو نه لزوماْ از مرتبه ی ۲ داشته باشیم، جمع آنها در قالب حالت های زیر انجام می گیرد

تعمیم حاصلضرب نقطه ای (داخلی) را می توان در قاعده ای موسوم به تنجش تانسور (tensor contraction) بکار گرفت، به صورتی که دو شاخص یکسان یکی هم وردا و دیگری پادوردا در یک تانسور مورد استفاده قرار گیرند. برای تانسورها، می توان انواع مختلفی از مشتق ها را تعریف کرد. اما پرکاربردترین آن ها به دو مورد مشتق معمولی (comma derivative) (مشتقی که در آنالیز تانسوری به صورت یک کاما در کنار آخرین شاخص هم وردا، آنرا نشان می دهند) و همچنین مشتق هم وردا (covariant derivative) ختم می شوند.

اگر هریک از مولفه های یک تانسور از مرتبه ی دلخواه، در یکی از دستگاه های مختصاتی صفر شوند، در دیگر دستگاه های مختصات نیز حتماْ صفر خواهند بود. لازم به ذکر است تبدیل متغیرهای یک تانسور، آنرا به تانسور دیگری تبدیل می کنند که مولفه هایش، توابع همگن خطی از مولفه های تانسور اولیه هستند.

فضای تانسوری از نوع می تواند به کمک حاصلضرب تانسوری فضای برداری (vector space tensor product) بین میدان برداری (vector fields) و میدان برداری دوگان نظیر یک شکلی ها (one-forms) نوشته شود. برای مثال

برابر با کلاف برداری - تانسوری بر روی خمینه ی (manifold) بوده که کلاف مماس و دوگان آن می باشد. تانسورهای نوع یک فضای برداری (vector space) را تشکیل می دهند. این توصیف به نوع تانسور دیگر نیز تعمیم پیدا می کند و نگاشت خطی وارون پذیر (invertible linear map) نگاشت را القاء می کند، فضای برداری دوگان (dual vector space) و ژاکوبی (Jacobian) است، که به شکل ذیل تعریف می شود

که نگاشت قلاب (pullback map) و ژاکوبی است که با جابجایی ژاکوبی به طرف دیگر معادله حاصل شده است. این تعریف میتواند به دیگر ضرب های تانسوری (tensor products) و بسط داده شود. هنگامی که یک تبدیل مختصات انجام می دهیم، متعاقباْ تانسورها نیز به کمک ژاکوبی (محصول تبدیل خطی تانسورها) تبدیل خواهند شد.

تانسور آفینی (Affine tensor)

تانسور آفینی (مستوی)، تانسوری متناظر با تبدیلات مختصات خطی است،، که در آن دترمینان مخالف با صفر است. این تبدیل از دستگاه مختصات راست گوشه به دستگاه مختصات دارای محورهای مایل (oblique axes) صورت می پذیرد. در این روش تانسور آفینی می تواند در قالب یک تانسور دکارتی (*) ظاهر شود.

این تانسورها دارای ژاکوبی های زیر هستند:

قوانین تبدیل تانسورهای (مماس) پادوردای آفینی عبارت اند از

و به همین ترتیب ادامه می یابد. قوانین تبدیل تانسورهای (هم بردار) هموردای آفینی نیز عبارت اند از

و همین روال ادامه خواهد یافت.

قوانین تبدیل تانسورهای مختلط ـ شاخص آفینی نیز به صورت زیر هستند:

(*) تانسور دکارتی: تانسوری در فضای ۳ بعدی اقلیدسی است. برعکس تانسورهای عمومی، هیچ تمایزی میان شاخص های هموردا و پادوردای تانسورهای دکارتی وجود ندارد. با این حال در فضاهای نااقلیدسی (مانند فضاهای لورنتزی)، تانسورها به این تمایز نیازمندند.

تانسور ریمان

تانسور ریمان (Riemann tensor) كه همچنين با نام تانسور انحناي ريمان - كريستوفل يا تانسور انحناي ريمان نيز مشهور است، يك تانسور 4 شاخصي بسيار مهم و كاربردي در نسبيت عام است. ديگر تانسورهاي نسبيتي مفيد مانند تانسور انحناي ريچي (Ricci curvature tensor) و تانسور انحناي اسكالر نيز از تانسور نشئت مي گيرند:

كه در آن ضرايب ارتباط (connection coefficients) و علامت كاما "," مشتق معمولی را نسبت به شاخص بعد از خودش نشان می دهد. در یک بعد داریم . در چهار بعد این تانسور ۲۵۶ مولفه دارد. با استفاده از روابط تقارنی،

تعداد مولفه های مستقل به ۳۶ تا کاهش می یابد. با تحمیل شرط

تعداد مختصه ها به ۲۱ عدد تقلیل می یابد. درنهایت با استفاده از

تعداد مولفه های مستقل ۲۰ تا خواهند شد.

به طور کلی تعداد مولفه های مستقل در n بعد توسط رابطه ی زیر داده می شود:

اعداد هرمی چهار - بعدی (four-dimensional pyramidal numbers) از کوچک به ترتیب عبارتند از ۰ و ۱و ۶و ۲۰و ۵۰و ۱۰۵و ۱۹۶و ۳۳۶و ۵۴۰و ... . تعداد اسکالرهای (scalars) ممکن که می توان آنها را از و ساخت، برابرند با

$S_n={1 for n=2; 1/(12)n(n-1)(n-2)(n+3) for n=1,n>2$

در جملات تانسور ژاکوبی (Jacobi tensor)

فرض می کنیم که

$D^~_s=partial/(partialx^s)-sum_(l){s u; l},$

که کمیت نماد کریستوفل نوع دوم (Christoffel symbol of the second kind) است. بنابراین

$R_(pqrs)=D^~_q{p r; s}-D^~_r{r q; s}.$

به ساده ترین شکل اش در N بعد تجزیه می شود:

تانسور ریچی

تانسور ریچی یا به صورت مشابه تانسور انحنای ریچی به صورت زیر تعریف می شود

که تانسور ریمان است.

به تعبیر هندسی این تانسور در واقع نرخ رشد حجم توپی وارهای متریکی را در یک چندگونا کنترل می کند.

انحنای اسکالر

انحنای اسکالر همچنین با نام اسکالر انحنا نیز شناخته می شود، به این صورت معرفی می شود

که تانسور متریک پادوردا و تانسور ریچی است.

تانسور اینیشتین

این تانسور عبارت است از

که تانسور انحنای ریچی و انحنای اسکالر یا نرده ای و بالاخره تانسور متریک را نشان می دهد. این تانسور تحت عمل دیورژانس هموردا همواره برابر صفر است. یعنی:

که نماد ; بر مشتق هموردا (Covariant Derivative) دلالت دارد.

تانسورها

مطالب مشابه :

تانسورها

نمونه سوالات وجزوه ریاضی عمومی

سرفصل کنکور کارشناسی ارشد مهندسی کامپیوتر

سرفصل مطالب به نقل از دانشجوی شریف

تانسورها

سرفصل کنکور کارشناسی ارشد مهندسی کامپیوتر

رئوس مطالب مورد آزمون کنکور کارشناسی ارشد کامپیوتر