روش خیام(هندسی) در حل معادله درجه 3

حدود 900 سال پیش ،خیام روشی هندسی برای حل معادله ي درجه ي سوم به شكل:

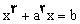() ارائه کرد که در اين جا به آن پرداخته ايم:

1)ابتدا یک سهمی به معادله ي را رسم می کنیم.

2)دایره اي به قطر رسم می کنیم ،به طوری که مرکز آن روی محور xها قرار داشته ودایره بر محور yها مماس باشد.(مانند آن چه که در شکل زیر آمده است.)

3)دایره ي رسم شده،سهمی رادرنقطه ي P قطع می کند،از P عمودی برمحور xها رسم کرده و نقطه ي تقاطع را Q می ناميم.

اندازه ي پاره خط AQ ريشه ي معادله است.

اثبات:معادله ي دايره ي به مركزو شعاع عبارت است از:.اگر اين دايره را با سهميقطع دهيم به معادله ي 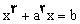مي رسيم و اين يعني اندازه ي پاره خط AQ ريشه ي معادله ي درجه ي سوم مزبور است.

روش خیام(هندسی) در حل معادله درجه 3

مطالب مشابه :

روش های حل معادله درجه 3

حل آسان معادله درجه 3

حل معادله ی درجه ی 3

حل معادلات درجه سوم آسان شد!

حل معادله درجه سوم

حل معادله درجه دوم

حل معادله درجه 3 و 4

روش خیام(هندسی) در حل معادله درجه 3