تبدیلات فوریه (1)

تبدیلات فوریه به طور کلی، تعمیم سری فوریه مختلط در حالتی است که حد 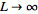برقرار باشد. این کار را می توان با تعویض سری مجزای با حاصل ضرب یک انتگرالده در دیفرانسیل متغیر آن و نیز فرض انجام داد. سپس سری را به شکل یک انتگرال می نویسیم و معادلات برابر خواهند بود با

در اینجا

که تبدیل فوریه ی پیشرو () نامیده می شود و

تبدیل فوریه وارونه () یا وارون تبدیل فوریه نامیده می شود. نماد در ترات (M.Trott) معرفی شده است (2004, p. xxxiv)، و و بعضی اوقات به ترتیب تبدیل فوریه و تبدیل فوریه ی وارونه نامیده می شوند که غالباْ با همین نام ها شناخته و مرسوم هستند (Krantz 1999, p. 202).

برخی از نویسندگان (خصوصاً فیزیکدانان) ترجیحاْ در نوشتار این تبدیل از بسامد زاویه ای به جای بسامد نوسان استفاده می کنند. اگرچه این به تقارن لطمه می که زوج تبدیلاتی زیر را نتیجه می دهد

برای برگرداندن تقارن تبدیلات، قرارداد

را بکار می گیریم که در برخی منابع از آن ها استفاده شده است (Mathews and Walker 1970, p. 102).

معمولاْ، زوج تبدیل فوریه ممکن است دو ثابت دلخواه و بکار برده شوند. مانند

هر تابعی را می توان همانند رابطه ی زیر به دو جزء زوچ و فرد تقسیم کرد

تبدیل فوریه را می توان همواره به صورت جملاتی از تبدیل cos فوریه (Fourier cosine transform) و تبدیل sin فوریه (Fourier sine transform) نوشت

که تابع یک تبدیل به جلو و یک تبدیل فوریه ی وارون را در برمی گیرد

(for continuous x را بخوانید پیوسته است در x)

۱- انتگرال وجود داشته باشد.

۲- تعداد ناپیوستگی ها، متناهی باشد.

۳- تابع در شرایط مرزی صدق می کند. لذا حداقل باید موید شرط کافی و ضعیف لیپ شیتس باشد. بنابر این شرط هر تابع با ازای هر در صادق باشد اگر

برای تمام ، که و مستقل باشند و و . همچنین به ازای تمامیها یک کران بالا محسوب می شود. در این صورت وجود خواهد داشت ای که متناهی باشد (Ramirez 1985, p. 29). همچنین هموار کننده ی یک تابع (تعداد مشتق های پیوسته ی بزرگتر) توسط تبدیل فوریه، فشرده می شود.

تبدیل فوریه یک تبدیل خطی است، برای اینکه اگر و به ترتیب تبدیل فوریه و باشند، آنگاه

بنابراین

تبدیل فوریه، همچنین متقارن است. زیرا و .

نماد به عنوان کانولوشن (convolution)، شناخته می شود. تبدیلات کانولوشن توابع منحصراً تبدیلات زیبا و جالبی هستند

جمله ی اول، به عنوان مشتق تبدیل فوریه مرسوم است. زیرا

که .

همچنین یک رابطه ی بسیار مهم و حیرت آور میان رابط خودکار (autocorrelation) و تبدیل فوربه وجود دارد که به قضیه ی وینر ـ خین چن (Wiener-Khinchin theorem) معروف است. فرض کنیم ، و همیوغ مختلط (complex conjugate) باشد. آنگاه تبدیل فوریه مجذور قدرمطلق (absolute square) برابر است با

منابع:

Arfken, G. "Development of the Fourier Integral," "Fourier Transforms--Inversion Theorem," and "Fourier Transform of Derivatives." §15.2-15.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 794-810, 1985.

Blackman, R. B. and Tukey, J. W. The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, 1959.

Bracewell, R. The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, 1999.

Brigham, E. O. The Fast Fourier Transform and Applications. Englewood Cliffs, NJ: Prentice Hall, 1988.

Folland, G. B. Real Analysis: Modern Techniques and their Applications, 2nd ed. New York: Wiley, 1999.

James, J. F. A Student's Guide to Fourier Transforms with Applications in Physics and Engineering. New York: Cambridge University Press, 1995.

Kammler, D. W. A First Course in Fourier Analysis. Upper Saddle River, NJ: Prentice Hall, 2000.

Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988.

Krantz, S. G. "The Fourier Transform." §15.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 202-212, 1999.

Mathews, J. and Walker, R. L. Mathematical Methods of Physics, 2nd ed. Reading, MA: W. A. Benjamin/Addison-Wesley, 1970.

Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994.

Morse, P. M. and Feshbach, H. "Fourier Transforms." §4.8 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 453-471, 1953.

Oberhettinger, F. Fourier Transforms of Distributions and Their Inverses: A Collection of Tables. New York: Academic Press, 1973.

Papoulis, A. The Fourier Integral and Its Applications. New York: McGraw-Hill, 1962.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, 1989.

Ramirez, R. W. The FFT: Fundamentals and Concepts. Englewood Cliffs, NJ: Prentice-Hall, 1985.

Sansone, G. "The Fourier Transform." §2.13 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 158-168, 1991.

Sneddon, I. N. Fourier Transforms. New York: Dover, 1995.

Sogge, C. D. Fourier Integrals in Classical Analysis. New York: Cambridge University Press, 1993.

Spiegel, M. R. Theory and Problems of Fourier Analysis with Applications to Boundary Value Problems. New York: McGraw-Hill, 1974.

Stein, E. M. and Weiss, G. L. Introduction to Fourier Analysis on Euclidean Spaces. Princeton, NJ: Princeton University Press, 1971.

Strichartz, R. Fourier Transforms and Distribution Theory. Boca Raton, FL: CRC Press, 1993.

Titchmarsh, E. C. Introduction to the Theory of Fourier Integrals, 3rd ed. Oxford, England: Clarendon Press, 1948.

Tolstov, G. P. Fourier Series. New York: Dover, 1976.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004.

Walker, J. S. Fast Fourier Transforms, 2nd ed. Boca Raton, FL: CRC Press, 1996.

می توانید برای دست یابی به منابع بزرگ تر به کتابخانه ی وبلاگ مراجعه کنید.

تبدیلات فوریه (1)

مطالب مشابه :

تبدیلات فوریه (1)

::آنالیز موجک :: WAVELET ::

کاربرد ریاضی(آنالیز موجک)

دانلود رایگان کتاب سری فوریه و تبدیل لاپلاس

آنالیز موجک :: WAVELET ::