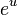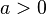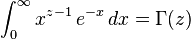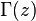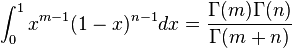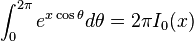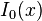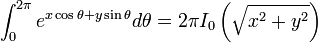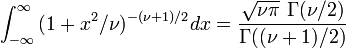انتگرال
اَنتِگرال (integral) مقدار مشترک ممکن زیرینۀ مجموعهای ریمانی و زبرینۀ مجموعهای ریمانی یک تابع حقیقی در بازۀ مفروض است. انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل میدهند.
نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.
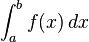
aو b نقاط ابتدا و انتهای بازه هستند و  تابعی انتگرالپذیر است و
تابعی انتگرالپذیر است و  نمادی برای متغیر انتگرالگیری است.
نمادی برای متغیر انتگرالگیری است.
از لحاظ تاریخی  یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرالگیری بر پایه متفاوتی پایه گذاری شده است.
یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرالگیری بر پایه متفاوتی پایه گذاری شده است.
انتگرال نامعین
تعریف:
هرگاه معادله دیفرانسیلی تابعی معلوم باشد و بخواهیم معادله اصلی تابع را معلوم کنیم این عمل را انتگرال نامعین نامیده و آن را با نماد نمایش میدهند. به انتگرال نامعین ضد مشتق نیز گفته میشود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات مشتقگیری است.
نمایش میدهند. به انتگرال نامعین ضد مشتق نیز گفته میشود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات مشتقگیری است.بنا به تعریف نماد
 را انتگرال نامعین نامیده وحاصل آن را تابعی مانند
را انتگرال نامعین نامیده وحاصل آن را تابعی مانند  در نظر میگیریم هرگاه داشته باشیم:
در نظر میگیریم هرگاه داشته باشیم: در واقع میتوان چنین بیان کرد:
در واقع میتوان چنین بیان کرد:
مثال: مقدار انتگرال تابع  را حساب کنید:
را حساب کنید:

انتگرال معین
بنا به تعریف، نماد  را انتگرال معین نامیده و حاصل آن را به ازای
را انتگرال معین نامیده و حاصل آن را به ازای  عددی به صورت زیر تعریف میکنیم:
عددی به صورت زیر تعریف میکنیم:
 و
و  به ترتیب، کرانهای بالا و پایین انتگرال نامیده میشوند.
به ترتیب، کرانهای بالا و پایین انتگرال نامیده میشوند.
تابع انتگرالپذیر
اگر تابعی دارای انتگرال باشد به آن انتگرالپذیر گویند.
تعبیر هندسی انتگرال
از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.
نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سهگانه معرف پارالل زیر نمودار است(غیرقابل تصور).
مثال
انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی  است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.
است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.

 نمایش گرافیکی انتگرال.
نمایش گرافیکی انتگرال.انتگرال یک تابع مساحت زیر نمودار آن تابع است.
انتگرال گیری
محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است. انتگرال را میتوان عمل برعکس مشتق معرفی نمود
مهمترین تعاریف در انتگرال[ویرایش]
از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ است. انتگرال ریمان بهوسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال ریمان–استیلتیس اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند:
محاسبه انتگرال :
اکثر روشهای اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:
1.f تابعی در بازه (a,b) در نظر میگیریم. 2.پاد مشتق f را پیدا میکنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر میگیریم:
بنابراین مقدار انتگرال ما برابر خواهد بود.
به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه میدهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار سادهای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتاند از :
- انتگرال گیری بهوسیله تغییر متغیر
- انتگرال گیری جزء به جزء :
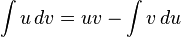
- انتگرال گیری با تغییر متغیر مثلثاتی
- انتگرال گیری بهوسیله تجزیه کسرها
روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار میرود همچنین میتوان بعضی از انتگرالها با ترفند هایی حل کرد برای مثال میتوانید به انتگرال گاوسی مراجعه کنید.
تقریب انتگرالهای معین[ویرایش]
محاسبه سطح زیر نمودار بهوسیله مستطیل هایی زیر نمودار. هر چه قدرعرض مستطیلها کوچک میشوندمقدار دقیق تری از مقدار انتگرال بدست میآید.
انتگرال هایی معین ممکن است با استفاده از روشهای انتگرال گیری عددی، تخمین زده شوند.یکی از عمومیترین روشها، روش مستطیلی نامیده میشود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقهای است. اگر چه روشهای عددی مقدار دقیق انتگرال را به ما نمیدهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما میکند.
کاربرد:
انتگرالها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک میتوان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست میآید. اما به طور کلی میتوان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیتها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته میشود:
![v=[L]/[T] t=[T] \!](http://www.bargozideha.com/static/portal/79/795379-602715.png)
سپس دو تحلیل را در هم ضرب می کنیم:
![[L] \!](http://www.bargozideha.com/static/portal/57/576429-386563.png)
پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.
انتگرالگیری یکی از دو عمل اصلی در حساب دیفرانسیل و انتگرال است. برخلاف دیفرانسیل که قواعد سادهای دارد که با استفاده از دیفرانسیل تابعهای سادهٔ مشابه یک تابع پیچیده، میتوان دیفرانسیل آن را یافت، انتگرالها اینگونه نیستند. از اینرو جدولهای انتگرال بسیار کاربردی هستند. این صفحه فهرست برخی از پرکاربردترین انتگرالها را دربردارد.
انتگرالها با یک تکینگی
انتگرال(تابع مشتقf×تابعg)+انتگرال(تابع مشتقg×تابعf)=تابعf×تابعg=== تابعهای گویا ===
انتگرالهای بیشتر : فهرست انتگرال توابع گویااین تابعها در نقطهٰ صفر برای a < -۱ یک تکینگی دارند.

 (Cavalieri's quadrature formula)
(Cavalieri's quadrature formula)


انتگرال(تابع مشتقf÷تابعg)ـانتگرال((تابع مشتقg×تابعf)÷تابعgبه توان2=ـ(تابعf÷تابعg)===تابعهای نمایی (توانی)===
انتگرالهای بیشتر : فهرست انتگرال تابعهای نمایی

تابعهای لگاریتمی
انتگرالهای بیشتر : فهرست انتگرال توابع لگاریتمی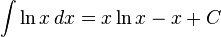
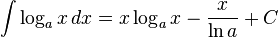
تابعهای مثلثاتی
انتگرالهای بیشتر : فهرست انتگرال توابع مثلثاتی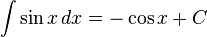
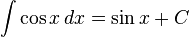
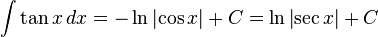
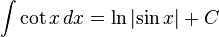

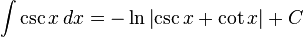
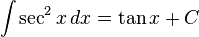
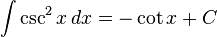
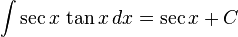
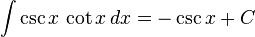
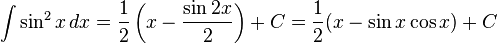
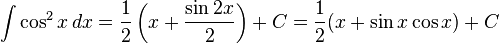
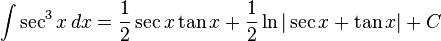 (ببینید انتگرال مکعب سکانت)
(ببینید انتگرال مکعب سکانت)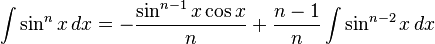
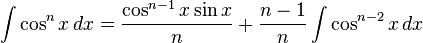
تابعهای مثلثاتی معکوس
انتگرالهای بیشتر : فهرست انتگرال توابع وارون مثلثانی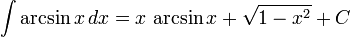
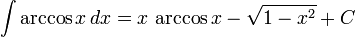

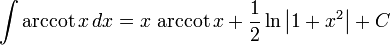
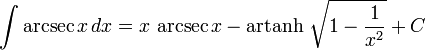
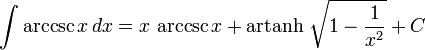
تابعهای هذلولوی
انتگرالهای بیشتر : فهرست انتگرال تابعهای هیپربولیک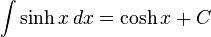
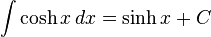
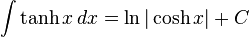
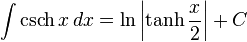
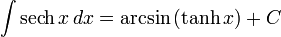
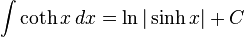
تابعهای هذلولوی معکوس
انتگرالهای بیشتر : فهرست انتگرال تابعهای وارون هیپربولیک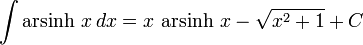
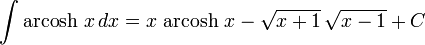

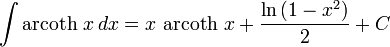
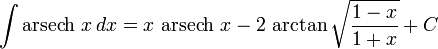
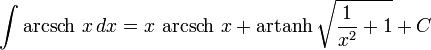
حاصل توابع نسبت به مشتق دومشان
تابعهای قدر مطلق
تابعهای مخصوص
Ci, Si: انتگرال مثلثاتی, Ei: انتگرال نمایی, li: انتگرال لگاریتمی, erf: تابع خطا






انتگرالهای معین
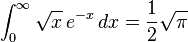 (همچنین ببینید تابع گاما)
(همچنین ببینید تابع گاما)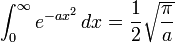 (انتگرال گاوسی)
(انتگرال گاوسی)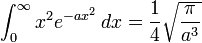 when a > 0
when a > 0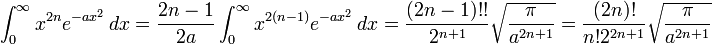 هنگامی که a > 0, n is 1,2,3,... و !! است فاکتوریل.
هنگامی که a > 0, n is 1,2,3,... و !! است فاکتوریل.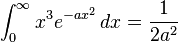 هنگامی که a > 0
هنگامی که a > 0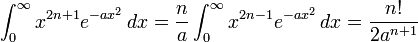 هنگامی که a > 0, n است 0, 1, 2, ....
هنگامی که a > 0, n است 0, 1, 2, ....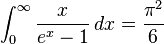 (همچنین ببینید Bernoulli number)
(همچنین ببینید Bernoulli number)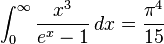
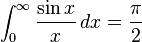 (see تابع سینک و انتگرال سینوسی)
(see تابع سینک و انتگرال سینوسی)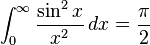
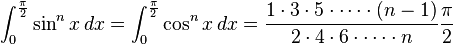 (if n is an even integer and
(if n is an even integer and 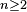 )
)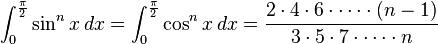 (if
(if  is an odd integer and
is an odd integer and 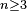 )
)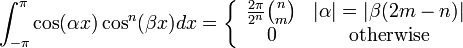 (for
(for 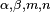 integers with
integers with 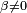 and
and 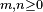 , همچنین ببینید Binomial coefficient)
, همچنین ببینید Binomial coefficient)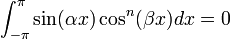 (for
(for 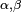 real and
real and  non-negative integer, همچنین ببینید تقارن)
non-negative integer, همچنین ببینید تقارن)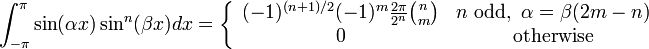 (for
(for 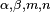 integers with
integers with 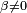 and
and 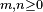 , همچنین ببینید Binomial coefficient)
, همچنین ببینید Binomial coefficient)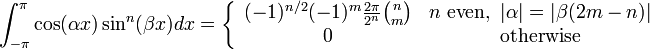 (for
(for 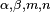 integers with
integers with 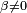 and
and 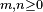 , همچنین ببینید Binomial coefficient)
, همچنین ببینید Binomial coefficient)![\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx=\sqrt{\frac{\pi}{a}}\exp\left[\frac{b^2-4ac}{4a}\right]](//www.bargozideha.com/static/portal/44/449714-714882.png) (where
(where ![\exp[u]](//www.bargozideha.com/static/portal/99/997817-359518.png) is the تابع نمایی
is the تابع نمایی 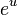 , and
, and 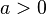 )
)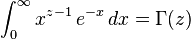 (where
(where 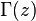 is the تابع گاما)
is the تابع گاما)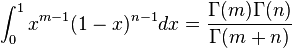 (the تابع بتا)
(the تابع بتا)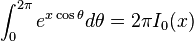 (where
(where 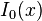 is the modified تابع بسل of the first kind)
is the modified تابع بسل of the first kind)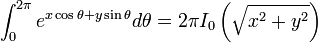
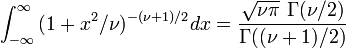 ,
, 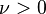 , this is related to the تابع چگالی احتمال of the توزیع تی-استیودنت)
, this is related to the تابع چگالی احتمال of the توزیع تی-استیودنت)
The method of exhaustion provides a formula for the general case when no antiderivative exists:

![\int_0^1 [\ln(1/x)]^p\,dx = p!](http://www.bargozideha.com/static/portal/26/269172-418196.png)
Start by using the substitution 
![I_p = \int_0^1 [\ln(1/x)]^p\;\mathrm{d}x = \int^{\infty}_0 \left[\ln(1/\operatorname{artanh}\,t) \right]^p \;\frac{\mathrm{d}t}{1 - t^2}](http://www.bargozideha.com/static/portal/76/765418-846153.png)
This brings the integral to the general form

which after integration by parts yields
![\left[f (\ln f)^n \right]^b_a - n \int^b_a (\ln f)^{n-1} f^'\;\mathrm{d}t](http://www.bargozideha.com/static/portal/40/401701-159195.png)
and provided the first term vanishes at the end points, we get the recurrence relation

which upon computation gives

Applying to our integral, we notice that
![[\ln(1/x)]^p = (-1)^p\;[\ln(x)]^p](http://www.bargozideha.com/static/portal/53/537126-797410.png)
Hence the final answer is:

مطالب مشابه :
انتگرال ریمان
دریای ریاضی - انتگرال ریمان - آموزش ریاضی، دانلود رایگان جزوه های دانشگاهی،کتاب های
انتگرال ریمان
انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته میشود.
انتگرال ریمان
ریاضیات دبیرستان - انتگرال ریمان - - ریاضیات دبیرستان این وبلاگ برای تمامی علاقمندان به
انتگرال
از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است.
اندازه و انتگرال لبگ
انتگرال لبگ (Lebesgue این انتگرال، دسته ی عظیمی از توابع انتگرالپذیر که انتگرال ریمان (Riemann
انتگرال
انتگرال معین بنا به تعریف، نماد را انتگرال معین نامیده و حاصل آن را به ازای عددی به صورت زیر
انتگرال و دعوای نیوتن و لایب نیتز
گنجینه ریاضی - انتگرال و دعوای نیوتن و لایب نیتز - علمی، پژوهشی، فرهنگی و انتشاراتی
برنهارد ریمان
دانلود کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry
انالیز ریاضی
در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه
برنهارد ریمان
دانلود رایگان کتب و جزوات ریاضی و هندسه - برنهارد ریمان - Mathematics and Geometry - دانلود رایگان کتب و
برچسب :
انتگرال ریمان




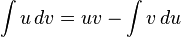

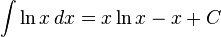
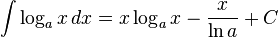
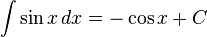
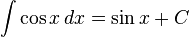
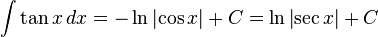
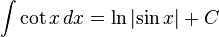

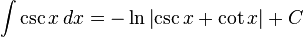
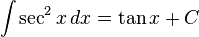
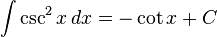
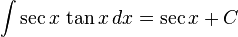
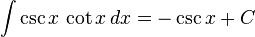
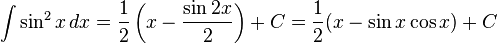
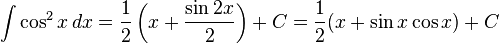
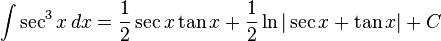
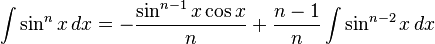
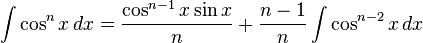
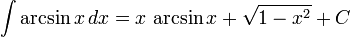
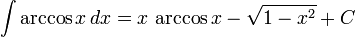

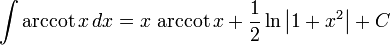
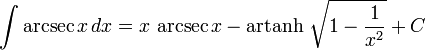
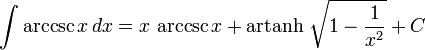
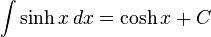
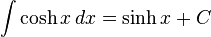
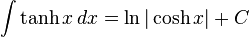
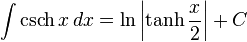
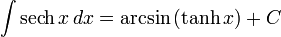
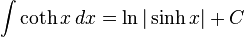
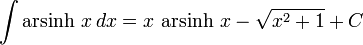
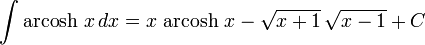

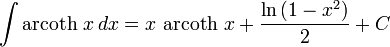
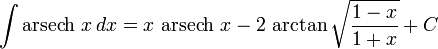
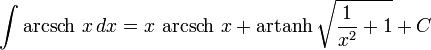




![\int \left| (ax + b)^n \right|\,dx = {(ax + b)^{n+2} \over a(n+1) \left| ax + b \right|} + C \,\, [\,n\text{ is odd, and } n \neq -1\,]](http://www.bargozideha.com/static/portal/46/464943-731633.png)


![\int \left| \tan{ax} \right|\,dx = {\tan(ax)[-\ln\left|\cos{ax}\right|] \over a \left| \tan{ax} \right|} + C](http://www.bargozideha.com/static/portal/37/374349-318757.png)


![\int \left| \cot{ax} \right|\,dx = {\tan(ax)[\ln\left|\sin{ax}\right|] \over a \left| \tan{ax} \right|} + C](http://www.bargozideha.com/static/portal/57/573920-341471.png)
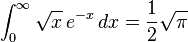
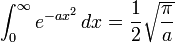
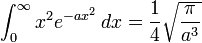
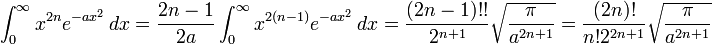
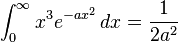
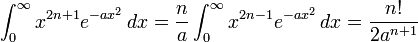
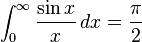
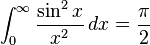
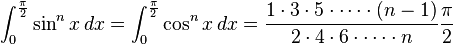
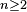

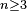
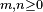
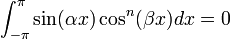
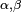

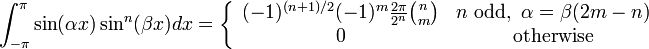
![\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx=\sqrt{\frac{\pi}{a}}\exp\left[\frac{b^2-4ac}{4a}\right]](http://www.bargozideha.com/static/portal/44/449714-714882.png)
![\exp[u]](http://www.bargozideha.com/static/portal/99/997817-359518.png)