نسبت طلائی
نسبت طلائی
دنیای اعداد بسیار زیباست و شما می توانید در آن شگفتیهای بسیاری را بیابید. در میان اعداد برخی از آنها اهمیت فوق العاده ای دارند، یکی از این اعداد که سابقه آشنایی بشر با آن به هزاران سال پیش از میلاد میرسد عددی است بنام “نسبت طلایی” یا Golden Ratio.
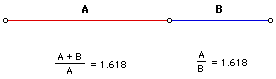
پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی a2=a*b+b2 را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا” 1.61803399 یا 1.618 خواهیم رسید.
شاید باور نکنید اما بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که بنظر میرسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد. این نسبت نه تنها توسط معماران و مهندسان برای طراحی استفاده می شود بلکه در طبیعت نیز کاربردهای بسیاری دارد که به تدریج راجع به آن صحبت خواهیم کرد.
اهرام مصر یکی از قدیمی ترین ساخته های بشری است که در آن هندسه و ریاضیات بکار رفته شده است. مجموعه اهرام Giza در مصر که قدمت آنها به بیش از 2500 سال پیش از میلاد می رسد یکی از شاهکارهای بشری است که در آن نسبت طلایی بکار رفته است. به این شکل نگاه کنید که در آن بزرگترین هرم از مجموعه اهرام Giza خیلی ساده کشیده شده است.
مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یاEgyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا” 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادل فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند i2=phi+b2 خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا” عدد طلایی را با phi نمایش می دهند )
طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا” معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد.
کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : “هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فيثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلايي می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد”.
تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه این مثلث به مثلث کپلر نیز معروف می باشد. کپلر پی به روابط بسیار زیبایی میان اجرام آسمانی و این نسبت طلایی پیدا کرد.
**********************************************
منبع :
وبلاگ گروهی معلمان ریاضی
استفاده از مطالب این وبلاگ با ذکر منبع بلا مانع است.
http://www.daneshriazi.blogfa.com
مطالب مشابه :
هنر تجلیگاه ریاضیات
مطلب درباره ی طبیعت سرچشمه زاینده و بی پایان است برای انگیزه دادن به هنرمند و
ریاضیات در آینهی اندیشهها
ریاضیات شانه بر زلف پریشان عالم است . حسینالهیقمشهای > قوانین طبیعت ، تفکرات ریاضی
تک درخت زیبا . . .
طبیعت ,شاندرمن , درباره ی خطبه سرا ی (تالش، دیار نا شناخته ها)
اندیشه های ریاضیدان ها
مطلب درباره ی
کوتاه وخواندنی تربیت کردن:
مطلب درباره ی طبیعت بهترین درسها را به بچه ها می دهد. ان ها را از طبیعت محروم نکنیم.
مقاله تاریخچه ی ریاضیات
مطلب درباره ی مقاله تاریخچه ی افکار فلسفی خود در روابط بین انسان و طبیعت غفلت
ریاضیدان از دید دکتر الهی قمشه ای
مطلب درباره ی ریاضی در طبیعت، در اقتصاد، در فیزیک، در رفتار و . به قول شاعر:
منشور در طبیعت
مثالی از کاربردمنشورها در طبیعت . مطلب جالب است که درباره ی چند ضلعیهای دیگر
نسبت طلائی
مطلب درباره ی استفاده می شود بلکه در طبیعت نیز کاربردهای بسیاری دارد درباره وبلاگ
برچسب :
مطلب درباره ی طبیعت