مبحث ماتریس

ماتریس

ماتریس به یک آرایش منظم از اعداد گفته می‌شود. به طوری که می‌توان گفت که هر ستون یا هر سطر یک ماتریس، یک بردار را تشکیل می‌دهد. در جبر خطی، می‌توان اثبات کرد که هر نگاشت خطیِ، از فضای 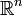${\mathbb{R}^n}$ به فضای ${\mathbb{R}^m}$ ، هم ارز (isomorph) با یک ماتریس $m\times n$ (m سطر و n ستون) می‌باشد. ماتریس‌ها کاربردهای فراوانی در جبر خطی دارند. از جمله در انتقال‌های خطی و در حل دستگاه معادلات خطی. ماتریس‌ها می‌توانند که با همدیگر جمع، از هم تفریق، در هم ضرب یا... (با قوانین خودشان) بشوند.

اگر دترمینان یک ماتریس مربعی نا صفر باشد، آنگاه آن ماتریس را ماتریس معکوس‌پذیر نامند.

درایه‌ها

به هر یک از عناصر موجود در یک ماتریس درایه می‌گویند. برای مشخص کردن هر درایه باید نام ردیف و ستون را در پایین نام ماتریس نوشت. برای مثال اگر نام ماتریسی i باشد درایه‌ای که در ردیف اول و ستون دوم قرار دارد به این صورت نشان داده می‌شود: i1,2

انواع ماتریس ها-قرینه ماتریس

May 30, 2010 | admin

آموزش ریاضیات:انواع ماتریس ها

ماتریس قطری چیست؟

تعریف ماتریس قطری:ماتریس مربع A را قطری می نامیم هرگاه,درایه های طرفین قطر اصلی آن صفر باشد.برای مثال ماتریس یک ماتریس قطری است.

ماتریس همانی چیست؟

تعریف ماتریس همانی:ماتریس مربعی را که درایه های قطر اصلی آن یک و سایر درایه های آن صفر باشد را ماتریس همانی (واحد) می نامیم و آن را با In یا Iنمایش می دهیم.

ماتریس های مساوی:

دو ماتریس را مساوی می گوییم هرگاه درایه های آن ها نظیر به نظیر باهم برابر باشند.

ماتریس های هم مرتبه:

دو ماتریس را که تعداد سطر ها و ستون های آن ها با هم برابر باشند ماتریس های هم مرتبه می گویند.

نکته ای که از این تعریف می توان نتیجه گرفت اینست که اگر دو ماتریس هم مرتبه نباشند,با هم مساوی نیستند.

ماتریس صفر:

هرگاه تمام درایه های یک ماتریس صفر باشد,آن را ماتریس صفر می نامند و با نماد نمایش می دهند.

تعریف قرینه ی ماتریس :

قرینه ماتریس A از قرینه کردن تک تک درایه های ماتریس A بدست می آید.قرینه ی ماتریس A را به صورت A- نمایش می دهیم.

ماتریس اسکالر

ماتریس قطری که تمام درایه‌های قطر اصلی ان برابر باشد یک ماتریس اسکالر نامیده می‌شود و برابر با همان مقدار درایه در ضرب ماتریس‌هاست یا به عبارت دیگر λIکه I ماتریس همانی است. برای مثال ماتریس ۳×۳ اسکالر به این شکل است:

$\begin{bmatrix} \lambda & 0 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda\end{bmatrix}.$

رای پیدا کردن معکوس ماتریس 3 در 3 ، ابتدا دترمینان آن را حساب می کنیم.اگر دترمینان مساویصفر باشد ، ماتریس معکوس وجود ندارد.

محاسبه دترمینان ماتریس 3 در 3

اگر ماتریس A را بصورت زیر در نظر بگیریم :

برای محاسبه دترمینان ماتریس A خواهیم داشت :

det(A)=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a12a21a33-a11a23a32

یا همانطور که در شکل زیر مشخص است ، ابتدا ماتریس را با تکرار دو ستون اول گسترش می دهیم و سپس درایه هایی را که با خطوط قطری به هم وصل شده اند و به آنها دسته اول می گوییم را در هم ضرب کرده و حاصلشان را با هم جمع می کنیم سپس درایه هایی را که با نقطه چین به هم وصل شده اند را در هم ضرب کرده و حاصلشان را از دسته اول کم می کنیم.

ترانهاده یک ماتریس 3 در 3

بعنوان مثال برای ماتریس A ترانهاده ماتریس مانند شکل زیر می شود :

محاسبه ماتریس الحاقی

برای بدست آوردن ماتریس معکوس ، باید ماتریس الحاقی ماتریس A را بدست بیاوریم . برای این کار بدین گونه عمل می کنیم :

ابتدا ترانهاده ماتریس A را بصورت زیر به ماتریس جدید B تبدیل می کنیم :

حال درایه ها را یکی در میان در - و + ضرب میکنیم :

حال معکوس دترمینان A را در B ضرب می کنیم .حاصل همان ماتریس معکوس ماتریس A است.

توضیحات کامل برای دانلود:

۱- تعریف ماتریس (دریافت فایل)

۲- جمع و تفریق دو ماتریس(دریافت فایل) ۳- ضرب یک عدد حقیقی در ماتریس(دریافت فایل) ۴- ضرب دو ماتریس

۴-۱) تعریف ضرب دو ماتریس(دریافت فایل)
۴-۲)خواص ضرب ماتریس(دریافت فایل)

۵- ماتریس های تعویض پذیر(دریافت فایل) ۶- تساوی دو ماتریس(دریافت فایل) ۷ – افراز ماتریسها(دریافت فایل) ۸- ماتریس ترانهاده یا جابجا شده(دریافت فایل) ۹- انواع ماتریسها
             ۹-۱) ماتریس قطری(دریافت فایل)
   ۹-۲) ماتریس واحد( همانی) وماتریس صفر(دریافت فایل)
   ۹-۳)ماتریس اسکالر(دریافت فایل)
   ۹-۴)ماتریس خود توان و ماتریس پوچ توان(دریافت فایل)
   ۹-۵)ماتریس متقارن وپادمتنقارن
   ۹-۵-۱)تعریف ماتریس متقارن وپادمتقارن(دریافت فایل)
   ۹-۵-۲)ویژگی های ماتریس متقارن وپادمتقارن(دریافت فایل)
   ۹-۶)ماتریس متعامد(دریافت فایل)
   ۹-۷)ماتریس بالا مثلثی و ماتریس پائین مثلثی(دریافت فایل)

۱۰-اثر ماتریس(دریافت فایل) ۱۱- دترمینان
   ۱۱-۱) تعریف دترمینان(دریافت فایل)
   ۱۱-۲)ویژگیهای دترمینان(دریافت فایل)
   ۱۱-۳)روشهای حل مسائل دترمینان
   ۱۱-۳-۱)دسته اول(دریافت فایل)
   ۱۱-۳-۲)دسته دوم(دریافت فایل)
         ۱۱-۳-۳)دسته سوم(دریافت فایل)

   ۱۱-۴) نمایش مساحت یک مثلث و معادله خط توسط دترمینان(دریافت فایل)
   ۱۱-۵)دترمینان حاصل ضرب ماتریسها(دریافت فایل)
   ۱۱-۶)دترمینان کهاد و همساز و ماتریس همساز و ماتریس وابسته یا الحاقی(دریافت فایل)

۱۲- ماتریس وارون (معکوس)
۱۲-۱) تعریف ماتریس وارون(دریافت فایل)
۱۲-۲) شرط لازم و کافی برای وارون پذیری یک ماتریس(دریافت فایل)
۱۲-۳) نکات مهم(دریافت فایل)

۱۳-چند جمله ای ماتریسی(دریافت فایل) ۱۴- دستگاههای معادلات خطی
   ۱۴-۱)مقدمه و تعریف(دریافت فایل)
   ۱۴-۲) دستگاههای هم ارز ( قاعده حذفی گوس )(دریافت فایل)
   ۱۴-۳) دستگاههای معادلات خطی و ماتریسها ( قاعده حذفی گوس- جردن )(دریافت فایل)
   ۱۴-۴) حل و بحث دستگاههایی که تعداد معادلات و تعداد مجهولات برابر دارند (دریافت فایل)
   ۱۴-۵) دستگاههای همگن(دریافت فایل)
   ۱۴-۶)حل دستگاهها به روش ماتریس وارون یا معکوس(دریافت فایل)
         ۱۴-۷) حل دستگاهها به روش دستور کرامر(دریافت فایل)

دانلود مباحث ماتریس

:http://math-dept.talif.sch.ir/files/extract_file.php?file_id=393

مبحث ماتریس

ماتریس

درایه‌ها

انواع ماتریس ها-قرینه ماتریس

ماتریس اسکالر

مطالب مشابه :

الگوریتم ضرب زنجیری ماتریس ها

انواع ماتریس ها

تعریف ماتریس ها

ماتریسها

محاسبه ماتریس ها

ماتریس

ماتریس ها

مبحث ماتریس

121- ماتریس هدف ها(OMAX)