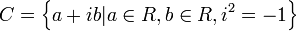اعداد مختلط

عدد مختلط

مقدمه

اعداد مختلط هنوز هم درنظر برخی با شک آمیخته با ترس همراه است. ولی درنظر ریاضیدانان امروزی این دستگاه صرفا گسترش مجموعه بنیاد ساده‌ای از اعداد حقیقی است. همیلتون (Hamilton) ریاضیدان قرن نوزدهم گسترشی برای اعداد مختلط پیدا کرد و آن را چهارگانها نامید. ماهیت ریاضیات جدید چنان است که باید دید خود را وسیعتر کنیم و به دستگاههایی اصل موضوعی بپردازیم که بافتهای ریاضی مفیدتری را بدست دهند. مفهوم عدد چیزی جز قسمتی از این برای کلی نیست. جبر جدید یا دستگاههایی اصل موضوعی سروکار دارد که ، بطور کلی متشکل از مجموعه‌هایی است همراه با عملهای مختلفی روی آن مجموعه‌ها. دوتا از این دستگاهها عبارتند از حلقه و میدان. اگر بخواهیم پا را از اعداد مختلط فراتر نهیم، مسیر پربار راه چهارگانهای همیلتون نیست بلکه مسیر ساختهای جبری تقسیم یافته جبر جدید است.

عدد مختلط عددی به شکل است که aو bاعداد حقیقی‌اند و iیکهٔ موهومی با خصوصیت i2 = -1است (در برخی از رشته‌ها مانند مهندسی برق، که در آن iنشانه شدت جریان است، iرا با jنیز نمایش می‌دهند). عدد aقسمت حقیقی و عدد bقسمت موهومی نامیده و نوشته می‌شود:

Imz = b

Rez = a

اعداد حقیقی را می‌توان به عنوان اعداد مختلط با قسمت موهومی صفر در نظر گرفت، یعنی عدد حقیقی aمعادل است با عدد مختلط a + 0i.

مجموعه اعداد مختلط را بصورت تعریف می‌کنیم.

کاربردها

تئوری کنترل

در تئوری کنترل معمولا سیستمها از فضای زمان توسط تبدیل لاپلاس به فضای دیگری انتقال پیدا می کنند که در این فضا ، معادلات دیفرانسیل بصورت جبری بیان می‌شوند.

پردازش سیگنال

اعداد مختلط برای پردازش سیگنالها به عنوان یک تعریف واضح از سیگنالهای با تغییرات نوسانی استفاده می‌شود. اندازه Zبرای تعریف دامنه و آرگومان آن برای تعریف فاز یک موج سینوسی با فرکانس معلوم استفاده می‌شود. اگر آنالیز فوریه برای نوشتن مقدار خطی یک سیگنال مشخص به صورت مجموع توابع تناوبی استفاده شود، این توابع تناوبی اغلب به شکل جزء حقیقی توابع مختلط نوشته می‌شوند.

مکانیک کوانتوم

اهمیت اعداد مختلط در مکانیک کوانتوم بخاطر این است که این تئوری بر اساس فضای بینهایت بعدی هیلبرت (Hilbert) پایه گذاری شده است.

تئوری نسبیت

در نسبیت عام و خاص می توان با موهومی گرفتن بعضی متغیرها در فضای زمانی به روابط ساده‌تری رسید.

معادلات دیفرانسیل

در معادلات دیفرانسیل معمول است که ابتدا ریشه‌های مختلط rبرای معادله ساختاری مربوط به یک معادله دیفرانسیل خطی را پیدا کرد و سپس در حل سیستم ، از تابع اساسی استفاده کرد.

مکانیک کلاسیک

از توابع مختلط برای حل جریان پتانسیل دو بعدی استفاده می‌شود.

کاربرد اعداد مختلط در مهندسی

مقدمه:

اجداد ما فرض کردند که عدد 1 وجود دارد ولی هیچ

فیزیکدانی ثابت نکرد 1 به عنوان یک مفهوم فیزیکی وجود دارد. همین فرض باعث به وجود آمدن علم حساب شد. علم هندسه هم به همین ترتیب با مفروض الوجود گرفتن نقطه به وجود آمده است .

عدد 1 وجود حقیقی ندارد و فقط وجودی ذهنی دارد .حال باید دید آیا فرض وجود 1 می تواند نیاز انسان را برای حل مشکلات خود برآورده سازد

در علوم طبیعی تنها می توان کمیاتی را به صورت حقیقی با هم جمع کرد و سایر عملیات روی آن را انجام داد که همه این کمیت ها از یک جنس باشند . برای ترکیب دو کمیت از دو جنس مختلف یکی از آنها را روی محور حقیقی و دیگری را روی محور موهومی نمایش می دهیم و کمیتی جدید تعریف می کنیم که یک کمیت ترکیبی است (مثل قد_وزن)

بدین ترتیب ما به یک عبارت ترکیبی می رسیم که بیانگر دو دیمانسیون متفاوت است که با هم ترکیب شده اند.

مطالب بالا تعریف کلی از مفهوم اعدادمختلط است.

اعداد مختلط هنوز هم در نظر برخی با شک امیخته با ترس همراه است ولی در نظر زیاضیدانان امروزی این دستگاه صرفا گسترش مجموعه بنیاد ساده ای از اعداد حقیقی است.

همیلتون(hamilton )ریاضیدان قرن 19میلادی گسترشی برای اعداد مختلط پیدا کرد و آن را جهارگانها نامید.

ماهیت ریاضیات جدید چنان است که باید دید خود را وسیعتر کرده و به دستگاه های اصل موضوعی بپردازیم که بافت های ریاضی مفیدتری به دست می دهند. مفهوم عدد چیزی جز قسمتی از این برای کلی نیست .جبر جدید با دستگاه ها ی اصل موضوعی سرو کار دارد که به طور کلی متشکل از مجموعه هایی است همراه با عمل های مختلفی روی آن مجموعه ها .دو تا از این دستگاه هاحلقه و میدان نام دارد. اگر بخواهبم پا را از اعداد مختلط فراتر بنهیم مسیر پر بار راه چهار گانهای همیلتون نیست بلکه مسیر ساخت های جبری تقسیم یافته جبر جدید است

برخی کاربرهای اعداد مختلط:

• متغیرهای مختلط در توابع بسل دارای کاربرد است از جمله استفاده آن در محاسبات میزان جذب و انکسار اطفاء نور است

• در بهینه سازی تولید ماهیان سرد آبی کاربرد دارد

• توابع مختلط با آرگومان ماتریسی در مخابرات چند کاربره و چند کاناله کاربرد دارد

• در حل مسائل تمرکز تنش در مهندسی عمران کاربرد دارد

• در حل مسائل الاستیسیته دوبعدی در مهندسی عمران کاربد دارد برقراری معادلات تنش ها و سازگازی در یک محیط الاستیسیته دوبعدی،با صرف نظر کردن از نیروهای حجم منجر به حل معادله بی هارمونیک 4uoدر کل محیط می شود . uتابع تنش ایری است که از مشتقات آن می توان میدانهای تنش ،کرنش و جابجایی را به دست آورد. محاسبه تابعuدر حوزه توابع حقیقی برای یک محیط با مرز و شرایط مرزی دلخواه کاری دشوار است ولی در حوزه توابع مختلط می توان جواب عمومی معادله را بر حسب توابع مختلط تحلیلی(z) و (z) محاسبه کرد .این توابع را در یک محیط الاستیسیته بایستی طوری به دست آورد که شرایز اولیه مسئله روی مرزهای محیط مورد نظر برقرار شود.

• در تئوری نسبیت خاص و عام میتوان با موهومی در نظر گرفتن برخی متغیرها در فضای زمانی به روابط ساده تری دست یافت

• در معادلات دیفرانسیل معمول است که ابتدا ریشه های مختلط rرا برای معادله ساختاری مربوط به یک معادله دیفرانسیل خطی پیدا کرد و سپس در حل سیستم از تابع اساسی به شکل

rt f(t)=eاستفاده کرد.

• اعداد مختلط در کامپیوتر برای گرافیک حرف های بسیاری دارد

• اهمیت اعداد مختلط در مکانیک کوانتوم به خاطر این است که این تئوری بر اساس فشای بینهایت بعدی هیلبرت (Hilbert)پایه گذاری شده است

• در مکانیک سیالات برای حل جریان پتانسیل دو بعدی استفاده می شود

• در تئوری کنترل (مکانیک سیالات ) معمولا سیستم ها از فضای زمان توسط تبدیل لاپلاس به فضای دیگری انتقال پیدا می کنند که در این فضا معادلات دیفرانسیل به صورت جبری بیان میشود.

• اعداد مختلط برای پردازش سیگنالها به عنوان یک تعریف واضح از سیگنال های با تغییرات نوسانی استفاده می شود. اندازه Z (|Z|)برای تعریف دامنه و آرگومان Z (arg(z)) برای تعریف فاز یک موج سینوسی با فرکانس معلوم استفاده می شود.اگر آنالیز فوریه برای نوشتن مقدار خطی یک سیگنال مشخصی به صورت مجموع توابع تناوبی استفاده شود این تابع تناوبی اغلب به شکل جزء حقیقی توابع مختلط به صورت

f(t)=zeiwtنوشته می شود که در آن wنشان دهنده سرعت زاویه ای و عدد مختلط zبیانگر فاز و دامنه می باشد

اعداد مختلط

مطالب مشابه :

توابع مخطلط

انواع تابع

اعداد مختلط

مجموعه تمرینات درس توابع مختلط

منابع توابع مختلط

بسط و سری

اعداد مختلط