ماتریس
| کاربرد در شبیه سازی، پردازش تصویر، و ترافیک و سازه های شهری، حل معادلات طولانی |
ماتریس را در ریاضیات وارد کرد.با توجه به آنکه در آن زمان ریاضیدانان
اغلب به دنبال مسائل کاربردی بودند کسی توجهی به آن نکرد.اما بعدها
ریاضیدانان دنباله ی کار را گرفتند تا به امروز رسید که بدون اغراق
می توان گفت در هر علمی به گونه ای با ماتریس سروکار دارند.یکی از
نقش های اصلی ماتریس ها آن است که آنها ابزار اصلی محاسبات عملی
ریاضیات امروزی هستند.درست همان نقشی که سایقا اعداد بر عهده داشتند.
از این نظر می توان گفت نقش امروز ماتریس ها همان نقش دیروز اعداد
است.البته ماتریس ها به معنایی اعداد و بردارها را در بردارند..بنابراین
می توان آنها را تعمیمی از اعداد و بردارها در نظر گرفت.در ریاضیات
کاربردی ماتریس ها از ابزار روزمره هستند.زیرا ماتریسها با حل دستگاه
معادلات خطی ارتباط تنگاتنگی دارند و برای حل ریاضی مسائل عملی
مناسب ترین تکنیک فرمول بندی مسئله و یا تقریب زدن جوابهای مسئله
با دستگاه معادلات خطی است که در نتیجه ماتریس ها وارد کار می شوند.
از جنبه ی نظری فیزیک امروزی که فیزیک کوانتوم است بدون ماتریس ها
نمی توانست بوجود آید.هایزنبرگ – اولین کسی که در فیزیک مفاهیم ماتریسها
را به کار برد- اعلام کرد."تنها ابزار ریاضی من در مکانیک کوانتوم به آن
احتیاج دارم ماتریس است".بسیاری از جیرهایی که تا به حال دیده اید مانند جبر اعداد مخنلط و جبر بردارها را با ماتریسها بسیار ساده می توان بیان کرد.
*************************************
ماتریس
ماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر 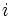 ام و ستون
ام و ستون  ام را با نماد
ام را با نماد  نشان میدهیم.
نشان میدهیم.
ماتریسی که دارای  سطر و
سطر و  ستون باشد را ماتریس از مرتبه
ستون باشد را ماتریس از مرتبه  در
در  مینامیم.(
مینامیم.(  )
)
نکته
هرگاه  آنگاه ماتریس را مربع از مرتبه
آنگاه ماتریس را مربع از مرتبه  مینامیم.
مینامیم.
یک ماتریس  را بصورت
را بصورت  نمایش میدهیم.
نمایش میدهیم.
تاریخچه
مطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد.
در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر اساس استفاده صریح از دترمینان ماتریس ضرایب معرفی گردیده است. در مقابل اولین استفاده ضمنی از ماتریسها توسط لاگرانژ برای تعیین ماکزیمم و مینیمم توابع چند مقداری مورد استفاده قرار گرفت. در ادامه گاوس روش حذفی خود را برای حل مسائل کمترین مربعات که کاربردهای بسیار وسیعی در علوم سماوی و ژئودوزی دارد را معرفی کرد.
روابط بین ماتریسها
تساوی دو ماتریس
دو ماتریس  و
و مساوی اند اگر و فقط اگر
مساوی اند اگر و فقط اگر  (هم مرتبه باشند) و
(هم مرتبه باشند) و
جمع دو ماتریس
قرینه ماتریس
اگر  آنگاه قرینه
آنگاه قرینه  را بصورت زیر تعریف میکنیم:
را بصورت زیر تعریف میکنیم:

ضرب اسکالر در ماتریس
اگر  و
و یک اسکالر باشد آنگاه
یک اسکالر باشد آنگاه
در ضرب اسکالر یک عدد در یک ماتریس ضرب میشود. در این نوع ضرب تمامی عناصر ماتریس در آن عدد ضرب میشوند به عنوان مثال:
و نمایش ریاضی آن به صورت زیر می باشد:
ضرب ماتریسها
اگر  و
و  آنگاه ضرب دو ماتریس را با علامت
آنگاه ضرب دو ماتریس را با علامت  نمایش داده و بصورت زیر تعریف خواهیم کرد:
نمایش داده و بصورت زیر تعریف خواهیم کرد:

در این نوع هر دو ضرب شونده و ضرب کننده از نوع ماتریس میباشند. بطور مشابه ضرب دو ماتریس نیز باید یک جنبه خوش تعریفی داشته باشد. ضرب دو ماتریس داده شده A و B زمانی خوش تعریف است که تعداد ستونهای ماتریس ضرب کننده با تعداد سطرهای ماتریس ضرب شونده برابر باشند. بر این ضرب دو ماتریس که شرایط قابل ضرب بودن را داشته باشند به صورت زیر بیان میشود:
برای بدست آوردن عنصر روی سطر iام و ستون y ام ماتریس خاصل ضرب عناصر روی سطر iام ماتریس ضرب کننده و عناصر روی ستون j ام ماتریس ضرب شونده را در نظر گرفته و آنها در هم ضرب و جمع می کنیم. به صورت ریاضی حاصلضرب دو ماتریس بصورت زیر نمایش داده می شود:
بطور سادهتر میتوان ماتریس ضرب کننده را به صورت مجموعه ای از بردارهای نظری و ماتریس ضرب شونده را به صورت مجموعهای بردارهای ستونی در نظر گرفت.
انواع ماتریس
ماتریس صفر
ماتریسی که تمام درایه های آن صفر باشد را ماتریس صفر نامیده و ماتریس صفر از مرتبه  را با نماد
را با نماد  نمایش میدهیم و داریم
نمایش میدهیم و داریم 
ماتریس همانی
ماتریس مربع  از مرتبه
از مرتبه  را همانی گوییم هرگاه
را همانی گوییم هرگاه وبه ازای هر
وبه ازای هر  داشته باشیم
داشته باشیم 
ماتریس اسکالر
اگر  یک اسکالر و
یک اسکالر و  ماتریس همانی از مرتبه
ماتریس همانی از مرتبه باشد آنگاه
باشد آنگاه  را ماتریس اسکالر مینامیم.
را ماتریس اسکالر مینامیم.
ماتریس وارون پذیر
ماتریس مربع  را وارون پذیر مینامیم هرگاه ماتریس مربع
را وارون پذیر مینامیم هرگاه ماتریس مربع  یافت شود به طوری که
یافت شود به طوری که  .دراین صورت
.دراین صورت  را وارون
را وارون  مینامیم.
مینامیم.
ماتریس قطری
ماتریس مربعی  را قطری نامیم هرگاه عناصر روی قطر اصلی همگی غیر صفر باشند و عناصر غیر از قطر اصلی صفر باشند.
را قطری نامیم هرگاه عناصر روی قطر اصلی همگی غیر صفر باشند و عناصر غیر از قطر اصلی صفر باشند.
چند خاصیت از ماتریس ها
اگر سه ماتریس
سه ماتریس  و
و دو اسکالر باشند آنگاه:
دو اسکالر باشند آنگاه:








اگر  آنگاه
آنگاه 
اگر  آنگاه
آنگاه 
اگر  انگاه
انگاه 
در حالت کلی ضرب ماتریسها خاصیت جابجایی ندارد.(حتی اگر  تعریف شده باشند و این در حالتی ممکن است که
تعریف شده باشند و این در حالتی ممکن است که دو مربع هم مرتبه باشند.)
دو مربع هم مرتبه باشند.)
ماتریس مربعی
ماتریسی است که تعداد سطرها و ستونهای آن با هم برابر باشد.
ماتریس سطری
ماتریسی است که یک سطر دارد. مثلا

ماتریس ستونی
ماتریسی است که یک ستون دارد. مثلا

ماتریسی است که فقط یک عضو دارد. مثلا

ماتریس صفر
تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است.

ماتریس واحد یا یکه
ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر میباشد. این ماتریس را با I نشان میدهند. مثلا

!ماتریس قرینه
اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند.
ماتریس قطری
ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا

ماتریس عددی یا اسکالر
ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا

ماتریس منفرد
ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی 
ماتریس غیرمنفرد یا وارونپذیر
اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد میگویند. یعنی 
ماتریس معکوس یا ماتریس وارون
ماتریس مربعی A را در نظر میگیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A میگویند معمولا ماتریس معکوس A را بصورت  نشان میدهند و در نتیجه داریم:
نشان میدهند و در نتیجه داریم:

ماتریس همسازه
اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست میآید که به آن همسازه میگویند. ماتریس همسازه A را با N نمایش میدهند.

برای هر  در ماتریس
در ماتریس  ، همسازه
، همسازه  برابر است با عدد
برابر است با عدد
کوفاکتور عضو 

بطوریکه ،  را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد.
را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد.
ماتریس وابسته یا الحاقی
به ترانسپوزه ماتریس همسازه A ماتریس وابسته A میگویند و آن را با  نشان میدهند.
نشان میدهند.
ماتریس متقارن
اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن مینامند بعبارت دیگر ماتریس A متقارن است در صورتیکه  باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند.
باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند.
ماتریس ضدمتقارن یا آنتیمتقارن
هرگاه قرینه ترانسپوزه ماتریس A برابر A شود، به آن ماتریس ضدمتقارن میگویند و داریم 
ماتریس پایین مثلثی
اگر در یک ماتریس مربعی تمام عضوهای بالای قطر اصلی صفر باشند به آن ماتریس پایین مثلثی میگویند یعنی 
ماتریس بالا مثلثی
اگر در یک ماتریس مربعی تمام عضوهای پایین قطر اصلی صفر باشند به آن ماتریس بالا مثلثی میگویند. یعنی
ماتریس متعامد
اگر در ماتریس مربعی A داشته باشیم  به ماتریس متعامد میگویند.
به ماتریس متعامد میگویند.
منبع: ریاضیات و فیزیک
**************************************
کاربرد ماتریس (رادارها)
هر رادار شامل یک آنتن گیرنده و یک آنتن فرستنده میباشددر این گونه از رادار ها به ازای هر آنتن فرستنده آنتن گیرنده هم وجود دارد که از تعداد زیادی انتن فرستنده و گیرنده تشکیل شده است

و

تر کیب اطلاعات دریافتی هر کدام گیرنده ها یا حساسه های موج و کنار هم قرار دادن آنها ماتریس یا آرایه ای دو بعدی بوجود میاورد چون بیشتر دریافت پژواک های بازگشتی از هدف مهم است میتوان به ازای هر فرستنده چند گیرنده در نظر گرفت با ایتن توضیح به نحوه کشف هدف و موقعیت یابی در این رادار ها نگاه میکنیم
این تصویر ماتریس گیرند های رادار در یک فریم میباشد که خالی از هر گونه پژواک است

اگر به ازای امواج ارسالی بهترین حالت از امواج دریافتی را معادل رقم 2 و رنگ سفید در نظر بگیریم و رقم 0 را رنگ سیاه و مکانهای بدون بازگشت
این تصویر نشانگر پالسهای بازگشتی از اهداف و یا اسمان است که دارای مقدار زیادی گین میباشد و اهداف در ان به وضوح دیده نمیشوند
که بصورت تصویر سیاه و سفید از صحنه مورد مشاهده رادار نشان داده شده است.و اهدافی که دور آن خط قرمز کشیده شده است اهدافی در فاصله دورتر هستند که براحتی قابل مشاهده نیستند.


حالا به تصویر رقمی گین ها نگاه کنید (گین مشابه همان پارازیت یا نویز میباشد ) در آن رقم های دو را مشاهده میکنید و ارقامی که کمتر از آن هستند حال با استفاده از برنامه ای اعداد ماتریس را میخوانیم و به ازای رقم های کمتر 0.5 عدد 0 قرار میدهیم ماتریس رقمی دست آمده این گونه است

که تصویر آن نیز بدین شکل است

بدین روش با استفاده از چندین گیرنده به تعداد زیاد توانسته ایم از امواج بازگشتی رادار تصویر سازی کنیم که به همین ترتیب هرچه تعداد خانه های ماتریس گیرنده های ما بیشتر باشد تصویر بدست واضح تر خواهد بود به حدی که میتواند شکل هواپیما را روی صفحه رادار نشان دهد.
برای یک حالت واقعی احتمالا فیلمی از تصویر رادار با 60 تا 30 فریم بر ثانیه خواهیم داشت که برنامه موقعیت یابی ما برای رصد اهداف و تعیین موقعیت آن در صفحه رادار باید 60 تا 30 بار در ثانیه محاسبات خود را روی این ماتریس ها انجام دهد (یعنی هر ماتریس بین 60 ت30 بار در ثانیه مجددا عدد گذاری می
مطالب مشابه :
الگوریتم ضرب زنجیری ماتریس ها
اندیشه نیک - الگوریتم ضرب زنجیری ماتریس ها - بنام خدایی که برای قلب دوست و برای اثبات دوستی
انواع ماتریس ها
ماتریس صفر. تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر
تعریف ماتریس ها
موضوع اساسی که برنامه متلب به آن می پردازد یک ماتریس است . یک ماتریس آرایه ای از اعداد است.
ماتریسها
ضرب ماتریسها اگر و آنگاه ضرب دو ماتریس را با علامت نمایش داده و بصورت زیر تعریف خواهیم کرد:
محاسبه ماتریس ها
ماتریس ها را می توان جمع یا تفریق کرد. (فقط در صورتی که اندازه ماتریس ها یکسان است.
ماتریس
ضرب ماتریسها. اگر و آنگاه ضرب دو ماتریس را با علامت نمایش داده و بصورت زیر تعریف خواهیم
ماتریس ها
!ماتریس قرینه اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر
مبحث ماتریس
انجمن جغرافیا دانشگاه آزاد واحد شهر ری - مبحث ماتریس - آموزش و به روز شدن اطلاعات و کاربردی
121- ماتریس هدف ها(OMAX)
دکتر رامبد باران دوست - 121- ماتریس هدف ها(omax) - وبلاگ شخصی
برچسب :
ماتریس ها



