مساحت دایره
مساحت یک دایره از فرمول زیر محاسبه می شود.

|
 |
اما این فرمول از کجا آمده؟ بگذارید پیدا کنیم.
کاری که می خواهیم انجام دهیم شکستن دایره به قسمتهای مساوی و بازآرائی آن به شکل مستطیل می باشد که مساحت آن را می دانیم.
عرض × طول = مساحت
ممکن است شما باور نکنید که می شود قطعات یک دایره را به مستطیل تبدیل کرد.
خوب، فقط نگاه کنید ... آسان است.
با دایره ای که می خواهیم بشکنیم شروع می کنیم.

حالا دایره را به چهار قسمت مساوی تقسیم می کنیم.
 |
 |
 |
 |
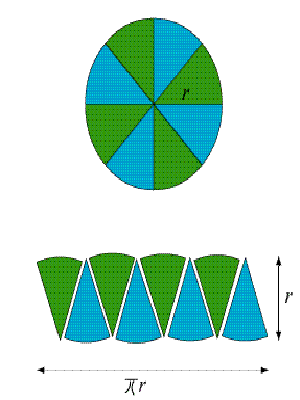
حالا آنها را طوری کنار هم می گذاریم تا یک مستطیل ایجاد شود.

دقیقاً یک مستطیل نیست، هست؟
اما کار ما هنوز تمام نشده، بگذارید دایره را به هشت قسمت مساوی تقسیم کنیم.
 |
 |
 |
 |
 |
 |
 |
 |
آنها را به شکل مستطیل مرتب می کنیم.

مطمئناً شروع کرده که شبیه یک مستطیل بشود، اما هنوز تا آنجا فاصله داریم.
قدم بعدی این است که به عقب برگردیم و دایره را به شانزده قسمت مساوی تقسیم کنیم.
قطعات اینجا هستند.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
این دفعه وقتی آنها را کنار هم قرار می دهیم. خیلی بیشتر مثل مستطیل به نظر می رسند، ببینید.

هدف ایجاد شکلی است که تا حد ممکن به مستطیل نزدیک باشد.
تا بتوانیم مساحت آن را با استفاده از فرمول مستطیل محاسبه کنیم.
عرض × طول = مساحت
اما این شکل اضلاع صاف ندارد، بنابراین فرمول حیلی دقیق نمی باشد.
بگذارید یک قدم جلوتر برویم و دایره راه به گروهی خرده های کوچک تقسیم کنیم. وقتی تمام قطعات را کنار هم قرار می دهیم، شکل مانند زیر به نظر می رسد.

این خیلی شبیه یک مستطیل کامل است. اما می توانید ببینید که بالا و پائین هنوز کاملاً صاف نیستند. آنها کمی دست انداز دارند.
می توانید تصور کنید که اگر باز هم به کارمان ادامه بدهیم چه اتفاقی خواهد افتاد؟ اگر به شکستن دایره به قطعات کوچکتر و کوچکتر ادامه دهیم؟
دست آخر، دست اندازها آنقدر کوچک می شوند که نمی توانیم آنها را ببینیم، و بالا و پائین شکل کاملاً مستقیم به نظر خواهند رسید. این چیزی است که خواهیم دید.

یک مستطیل کامل. حالا تمام کاری که باید انجام دهیم پیدا کردن مساحت مستطیل با استفاده از فرمول عرض × طول = مساحت می باشد.

سوال بعدی این است که، طول و عرض مستطیلی که از قطعات دایره ایجاد شده چه اندازه ای دارند؟
اجازه بدهید به عقب برگردیم، تا شما قطعات دایره را واضحتر ببینید.

طول بیرونی دایره اصلی، مسافت پیرامون دایره، یا محیط دایره می باشد.

نصف این مسافت پیرامون، در بالای مستطیل و نصف دیگر آن در پایین قرار می گیرد.

به عبارت دیگر، تمام تکه های آبی و قرمز برابر محیط دایره می باشند.
کناره های مستطیل درست شعاع هر قطعه یا شعاع دایره می باشند.
حالا می توانیم مساحت شکل را با فرمول مستطیل محاسبه کنیم.

... و در اینجا ما فرمول مساحت دایره ای را که با آن شروع کردیم، داریم.
الگوی پرورش کاوشگری
این الگو باعث آموزش علمی به سبک های مشخص و آموزش مفاهیم بنیادی در دانش آموزان می گردد . رسالت معلم در این الگو پرورش کاوشگری ،ایجاد جوی توأم با همکاری و داشتن انعطاف است .این الگو منجر به دانش علمی ،تعهد به کاوشگری علمی ،ژرف اندیشی و روح مهارت همکاری در دانش آموزان می شود .
مراحل این الگو عبارتند از :
1- فراهم آوردن زمینه جستجو برای دانش آموزان
2- تعیین مسئله از سوی دانش آموزان
3- مشخص کردن مسئله در هر جستجو توسط دانش آموزان
4- دانش آموزان به حدس در خصوص راههای توضیح مشکل می پردازند
برای درک بهتر الگو به یک موقعیت واقعی تدریس از این الگو توجه فرمائید .
نام درس: ریاضی
موضوع درس :مساحت دایره ،کلاس پنجم ابتدائی،
هدف کلی :آشنا شدن دانش آموزان با چگونگی به دست آوردن مساحت دایره
هدف های(جزئی-رفتاری ):
انتظار می رود دانش آموزان پس از گذراندن این درس بتوانند :
1- رابطه بین مساحت دایره و مستطیل را درک نمایند .
2- رابطه بین مساحت دایره و متوازی الاضلاع را بفهمند
3- رابطه بین عرض مستطیل و شعاع دایره را تشخیص بدهند .
4- رابطه بین طول مستطیل و محیط دایره را بیان کنند و تشخیص دهند .
5- چگونگی به دست آوردن مساحت دایره را عمل کنند و توضیح دهند
6- قاعده به دست آوردن مساحت دایره را در تمرین ها به کار ببرند
7- مسائل مربوط به رابطه بین مساحت دایره و متوازی الاضلاع نظیرش را حل نمایند .
8- مساحت شکل های هندسی ترکیبی را به دست آورند .
9- مسئله های مربوط به محیط و مساحت دایره را حل نمایند
10- از روی اندازه های قاعده و ارتفاع متوازی الاضلاع مساحت دایره نظیر آن را به دست آورند .
11- نسبت به چگونگی به دست آوردن مساحت دایره علاقه مند شوند
وسایل آموزشی : دایره های رسم شده ،خط کش ،قیچی ،مستطیل ،متوازی الاضلاع،گچ سفید و رنگی ،کتاب ریاضی –تخته کلاس ،تجربیات دانش آموزان
ارزشیابی تشخیصی :
1- مساحت مستطیلی را که طول آن 12 سانتی متر و عرض آن 10 سانتی متر می باشد را به دست آورید .
2- محیط دایره ای که شعاع آن 5 سانتی متر می باشد چند سانتی متر مربع است
3- شعاع دایره ای 7 سانتی متر است .محیط دایره را به دست آورید .
4- مساحت مستطیلی 120 سانتی متر مربع است اگر طول این مستطیل 12 سانتیمتر باشد عرض این مستطیل چند سانتی متر است.
5- مساحت متوازی الاضلاع که ارتفاع آن 5 و قاعده آن 8 سانتی متر می باشد چند سانتی متر مربع است؟
روش های تدریس :
کاوشگری علمی ،تلفیقی ،پرسش و پاسخ ،گفتاری از طریق روش مجسم ،نیمه مجسم و مجرد
آمادگی و ایجاد انگیزه :
در جلسه قبل از تدریس از کلیه دانش آموزان خواسته می شود که د ایره ای بر روی مقوا رسم کرده و همراه خود به کلاس بیاورند. قابل ذکر است که چون شاگردان گروه،گروه می باشند از هر گروه خواسته می شود که دایره ای را با اندازه ای که داده می شود رسم نمایند .مثلا گروه 1-2-3 دایره ای به شعاع 5 سانتیمتر و گروههای دیگر کلاس دایره ای به شعاع 8 سانتیمتر رسم نمایندو با همراه داشتن قیچی و خط کش در کلاس حضور داشته باشند .
بعد از دعای آغازین ،احوالپرسی و حضور و غیاب برای ایجاد انگیزه و جلب توجه شاگردان ،خواسته می شود که مساحت متوازی الاضلاع ،مستطیل که بر روی مقوا رسم شده است را به دست آورند و شاگردان در حین پاسخگویی توضیحات لازم را نیز می دهند .بعد از کلیه شاگردان خواسته می شود محیط دایره هایی را که خود رسم کرده اند به دست آورده در ورقی که جلوی خود دارند ثبت نمایند تا مورد بررسی قرار گیرد .
هدف زمینه سازی برای ایجاد یک ارتباط ذهنی بین مطالب فرا گرفته شده و مطالبی که آموزش داده خواهد شد و استفاده از یادگیری های قبلی شاگردان برای حل مسائل جدید.
ارائه مطلب :
معلم :بچه های عزیز دایره های خود را بر روی میز قرار دهید .بعد از قرار دادن قطر دایره خود را رسم نمایید دانش آموزان قطر دایره را رسم می نمایند .دانش آموزان می گویند آیا برای دایره های خود می توانیم چند قطر رسم کنیم ؟در جواب معلم بله می گوید.معلم:آیا می توانید برای دایره خود 12 قطر رسم کنید ؟ دانش آموزان با کمی فکر در جواب بله می گویند .معلم شاگردان را راهنمایی می نماید که با دقت و با فاصله های منظم قطرهای دایره خود را رسم نمایند .گروههای 1و2و3 هر کدام (4 قطر )برای دایره خود رسم نمائید و گروههای دیگر کلاس 8 قطر با دقت رسم نمایید .دانش آموزان قطرهای دایره خود را رسم نمودیم .معلم :بسیار خوب .دانش آموزان :گروههایی که چهار قطر رسم کرده بودند دایره ها باید هشت قسمت شوند ؟معلم :بله .
دانش آموزان : گروههایی که هشت قطر رسم کرده بودند،دایره ما باید 16 قسمت شود؟معلم :بله .معلم :شاگردان راهنمایی می شوند که از روی قسمتهای ایجاد شده بر روی دایره (شعاع )با قیچی برش هایی ایجاد نمایند .دانش آموزان : گروههایی که چهار قطر رسم کرده بودند برش های ما 8 تکه می باشد معلم :بله .دانش آموزان : گروههایی که 8 قطر رسم کرده بودند برش های ما 16 تکه می باشد معلم :بله . شاگردان راهنمایی می شوندکه قسمتهای برش داده شده به چه طریقی در کنار هم گذاشته شود .
دانش آموزان :شکل ما شبیه به متوازی الاضلاع شده است . معلم :بله ،آفرین . دانش آموزان :شکل ما شبیه به مستطیل شده است . معلم :بله ،آفرین . دانش آموزان :چطور دایره ما به این شکل درآمده ؟ چه اتفاقی افتاد ؟معلم :دقت کنید
دانش آموزان :ما برای درست کردن مستطیل شعاع دایره خود را می بریدیم معلم :بله
دانش آموزان : در حقیقت شعاع دایره ما همان عرض مستطیل ما می باشد معلم :بله
دانش آموزان : ما هم برای متوازی الاضلاع شعاع دایره خود را برش دادیم: معلم :بله
دانش آموزان : پس ارتفاع متوازی الاضلاع همان شعاع دایره می باشد : معلم :بله
دانش آموزان : پس طول مستطیل چه قسمتی از دایره است ؟معلم:دقت کنید
دانش آموزان : آیا دور تا دور دایره ما (محیط دایره)در طول مستطیل قرار دارد؟معلم:سوال خود را با دقت بیشتر مطرح نمایید. دانش آموزان :دور تا دور دایره ما در دو طول مستطیل قرار دارد ؟معلم:بله .دانش آموزان می توانیم بگوییم نصف محیط دایره در یک طول مستطیل جا دارد ؟ معلم:بله .دانش آموزان : پس برای مستطیل که می گوییم طول × عرض می توانیم جایگزینی در دایره برای آن قرار دهیم . معلم :بله . دانش آموزان:طول × عرض یعنی همان نصف محیط × شعاع
معلم :بسیار خوب (شاگردانی که متوازی الاضلاع رسم کرده اند به همین طریق به ارتفاع و قاعده در متوازی الاضلاع می رسند که برابر همان طول و عرض می باشد )معلم شاگردان را راهنمایی می کند به محیط دایره که از قبل فرا گرفته اند )
دانش آموزان :محیط دایره یعنی (قطر ×14/3)معلم :بله. دانش آموزان :آیا می توانیم به جای نصف محیط معادل آن را قرار دهیم ؟معلم:بله ،بسیار خوب. دانش آموزان نصف یعنی یک دوم . معلم :بله شاگردان :پس می توانیم به جای نصف محیط بگوییم 14/3 ×قطر یک دوم . معلم:بله ،به جای یک دوم ،معادل آنرا قرار دهید . معلم: بسیار عالی دانش آموزان :چون عرض مستطیل نیز همان شعاع دایره بوده است .پس عرض ×طول یعنی همان 14/3 × شعاع ×شعاع . معلم :بله ،پس بچه های عزیز مساحت دایره شما از چه طریقی به دست می آمد؟دانش آموزان :مستطیل ،پس قاعده به دست آوردن مساحت دایره شعاع × شعاع ×14/3 .
ارزشیابی :
بچه ها ضمن خسته نباشی چند سوال برای تثبیت یادگیری شما تهیه کرده ام و از شما می خواهم که جواب بدهید .
1-مساحت دایره ای که شعاع آن 10 سانتی متر باشد چند سانتی متر مربع است ؟
2- مساحت دایره ای به قطر 8 سانتی متر چند سانتی متر مربع می باشد ؟
3-اگر ارتفاع متوازی الاضلاع 9 سانتیمتر باشد ،مساحت دایره نظیر آن چند سانتی متر مربع است ؟
4-اگر عرض مستطیل 7 سانتیمتر باشد ،مساحت دایره نظیر آن چند سانتی متر مربع است ؟
ارائه تکلیف :
دانش آموزان عزیز علاوه بر تمرینات کتاب به سوالات تکثیر شده نیز پاسخ می دهند .
معلم به سلیقه خود و با توجه به کیفیت یادگیری دانش آموزان در درس مساحت دایره اقدام به نوشتن چند سوال و تمرین برای تکالیف خارج از کلاس می نمایند .
تقریب هندسی عدد پی
دایره ای به شعاع 1 واحد در نظر بگیرید . همان طور که در شکل زیر می بینیم مساحت چند ضلعی های منتظم محاط در این دایره با افزایش تعداد ضلع ها به سمت مساحت دایره که همانا عدد پی می باشد ، نزدیک و نزدیک تر می شوند .
منبع: سایت رشد
مطالب مشابه :
شعاع دایره محیطی و محاطی
محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محاطی مثلث را با حرف r نشان می دهیم .
دایره
محاسبه ی شعاع دایره ی محاطی شعاع دایره ی محیطی مثلث را با حرف r نشان می دهند .
روش محاسبه سطح مثلث و اشکال هندسی
برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و دایره c به مرکز O و شعاع oB را قاعده ی مخروط
تشابه دوشکل هندسی
محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محیطی مثلث را با حرف r نشان می دهند .
مساحت دایره
حالا می توانیم مساحت شکل را با فرمول مستطیل محاسبه کنیم. 3- شعاع دایره ای 7 سانتی متر است
مثلث و دایره ، چند ضلعي منتظموچند نكته تكميلي
محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محیطی مثلث را با حرف r نشان می دهند .
برچسب :
محاسبه شعاع دایره