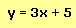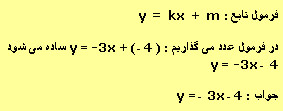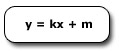|
|
|  |
|
|
|  |
|
|
| 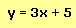 |
|
|
|  |
|
|
|  |
|
|
|  |
|
|
|  |
|
|
|  |
|
|
|  |
 |
|
4.2 |
تابع خط مستقیم (معادله خط) |
با
آگاهی داشتن دو چیز از خط تابع مستقیم ما می توانیم تشخیص بدهیم که خط در
کجای دستگاه محور مختصات قرار گرفته است. ما همچنین می توانیم با نگاه
کردن به یک خط مستقیم تابع آن را تعیین کنیم.
آن دو چیز مهم عبارتند از:
- (شیب خط)
k = ضریب که شیب (جهت) تابع را نشان می دهد.
- (موقعیت خط)
m = نقطه ای است که تابع محور
yرا قطع کرده و موقعیت آن را نمایش می دهد.
فرمول خط تابع مستقیم
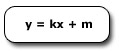
ضریب جهت
″ ضریب x″ تعیین کننده ی شیب خط بر روی دستگاه مختصات است. اگر دو تابع هر دو یک عدد را ضریب xداشته باشند، جهت آن دو بر روی دستگاه یکی
و موازی خواهد بود.
به مثال زیر توجه کنید:
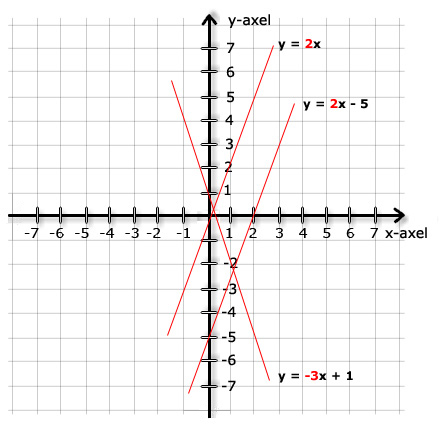 |
 |
با بررسی یک خط (بردار) روی دستگاه محورهای مختصات شما می توانید شیب آن را تشخیص بدهید. امتحان می کنیم:
نموداری را در زیر می بینید، ما می خواهیم جهت خط را پیدا کنیم. اگر ما یک پله روی محور xبه سمت راست برویم چه اتفاقی می افتد؟ xبه اندازه یک رقم بزرگترمی شود.
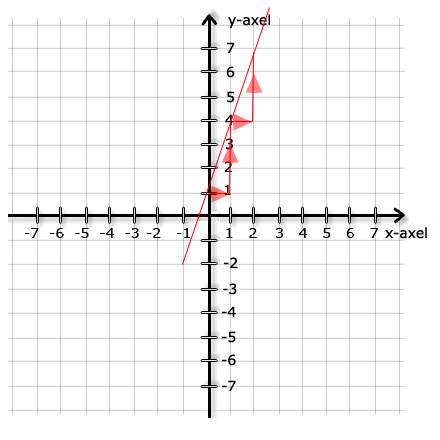
ملاحظه می کنید برای هر پله
ای که روی محورx
به سمت راست می رویم،
y سه واحد بزرگترمی
شود به عبارت دیگرy
در مقابل یک واحد بالا رفتن ارزش
x سه واحد بزرگتر می
شود. بنابراین نتیجه می گیریم که ضریب
x
یا ضریب شیب 3 است.
روش دیگر تخمین ضریب
X
این است که با مختصات دو نقطه آشنا باشید:
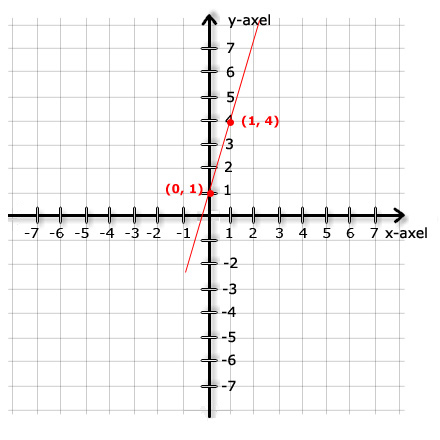
ما نقطه های (1, 0) و (4, 1) را می شناسیم.
الان می خواهیم شیب خط ما بین دو خط
را حساب کنیم. ما از نقطه (1, 0) شروع می کنیم.
ارزش مقداری x از 0 به 1 تغییر میکند, به بیانی دیگر
تغییرات برابر با 1+ میباشد.
ارزش مقداری y از 1 به 4 تغییر میکند, به بیانی دیگر
تغییرات برابر با 3+ میباشد.

ضریب شیب جهت :k
k = |
y متغییرات
در |
= |
+ 3 |
= + 3 |
 |

|
x متغیرات در |
+ 1 |
ضریب شیب جهت 3+ هست که ما در موقع جا
بجائی فلش در محور مختصات هم بدست آوردیم. |
 |
نقطه تقاطع با محورy :
حالا ضریب شیب جهت خط را می توانی محاسبه کنی و الان می
خواهیم یاد بگیریم که چگونه نقطه تقاطع با محورy را
بدست بیاوریم. اگر شما به عکس اول در این بخش را نگاه کنید, می بینید که دو
تا از خطها همان جهت ضریب شیب 2 دارند. اما آنها نقطه تقاطع مشترکی ندارند,
حالا ما می خواهیم ارزش مقداری موقعیت آنها را حساب کنیم.
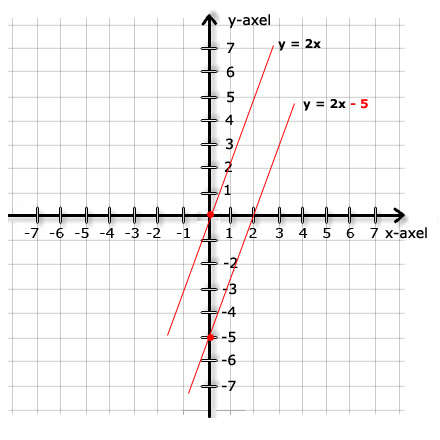
درکجا خط محورy
را قطع می کند؟
ارزش مقداری y توسط عدد
ثابت تابع تعیین می شود. در مثال بالا خط اول محورy
را در 0=y و درخط دومی 5-=y
قطع می کند. این عدد ثابت تابع می باشد که نقطه تقاطع خط محورy
می باشد.
m = عدد ثابت

در نمودار زیر موقعیت تقاطع خط شیب
را در محورy حساب می کنیم:
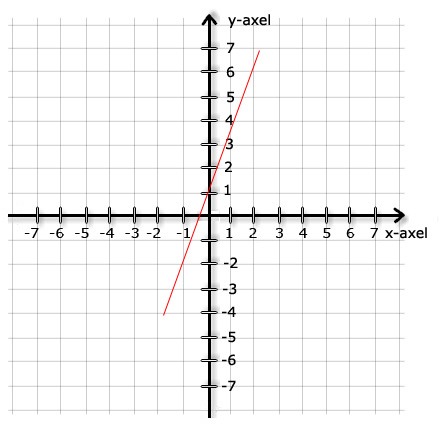
با نگاه کردن به اینکه در کجا محور
y قطع می شود ما می توانیم عدد ثابت m
را بدست آوریم. ما می بینیم که درنقطعه قطع محور y
ارزش مقداری y برابر با 1 می باشد. ما می توانیم هر
دو جهت خط و موقعیت خط را محاسبه کنیم :
k = 3
m = 1
بنابراین تابع طبق فرمول زیر محاسبه می
شود.
y = 3x + 1
ریاضیدانان فرمولهای زیادی را برای
محاسبه تابع خطی نوشتند. ما در آینده از فرمولی که در شروع بخش نشان
دادیم استفاده خواهیم کرد.
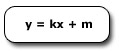
k ضریبی است که شیب (جهت) تابع را نشان می دهد.
mنقطه ای است که تابع محور
yرا قطع
می کند.
|
 |
|
 |
مطالب مشابه :
شیب خط
منشور علم - شیب خط - - منشور علم با بررسی یک خط (بردار) روی دستگاه محورهای مختصات شما می
.:: معادله های خطی ::.
شیب خط: (gradient of a line) شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با
شیب خط
شیب خط: (gradient of a line) شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با
آموزش ریاضی سوم - معادله خط
شیب خط: (gradient of a line) شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با
آموزش مقدماتی رگرسیون با نرم افزار اکسل
گزینه چهارم برای رسم خط در فضای مقابل fx فرمول مورد نظر نوشته شده است و شیب خط در
انیمیشن مفهوم شیب خط پایه سوم
ریاضی متوسطه دوره اول - انیمیشن مفهوم شیب خط پایه سوم - ریاضی و مدرسه - ریاضی متوسطه دوره اول
فلش های آموزشی (شیب و معادله خط)
مباحث متنوع رياضي و . . . - فلش های آموزشی (شیب و معادله خط) - ياد داشت هاي روزانه علیرضا حافظی
معادله ی خط
شیب خط: (gradient of a line) شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با
انیمیشن مفهوم شیب خط پایه نهم
شیب خط یعنی نسبت تفاضل عرض های دو نقطه (روی خط) به تفاضل طول های همان دو نقطه. در تصویر زیر
برچسب :
شیب خط