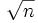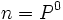عدد اول
اعداد اول:
تعریف:عدد طبیعی P>1 را عدد اول می گویند هرگاه تنها مقسوم علیه های مثبت آن 1 و P باشند. به عبارت دیگر یک عدد طبیعی اول است هرگاه جز یک و خودش بر هیچ عدد دیگری بخش پذیر نباشد.
هر عدد طبیعی مخالف یک که اول نباشد مرکب یا تجزیه پذیر می گوییم.
به عنوان مثال اعداد 2و3و5و7 اول و اعداد 12و18و325 مرکب می باشند.
- لازم به ذکر است که عدد یک نه اول و نه مرکب است و تنها عدد اول زوج عدد 2 است.
اگر n عددی مرکب باشد می توان گفت:
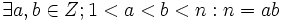
- نتیجه: اگر P عددی اول . a و b اعدادی طبیعی باشند، در این صورت:

برهان:
چون P عددی اول است بنابراین تنها دو مقسوم علیه متمایز دارد. از اینکه P=ab و aنتیجه می شود a , b دو مقسوم علیه متمایز P می باشند چون: a|P ,b|P و بنابر تعریف a=1 , b=P خواهد بود.
- حال به بیان چند قضیه مهم در باره اعداد اول می پردازیم:
- قضیه 1) هر عدد صحیح بجز یک و منفی یک دارای حداقل یک مقسوم علیه اول است.
فرض می کنیم a عددی صحیح باشد که مخالف یک و منفی یک است. اگر a=0 باشد در این صورت تمامی اعداد صحیح از جمله اعداد اول a را می شمارند و حکم برقرار است. حال فرض می کنیم a مخالف صفر باشد و نشان می دهیم a دارای حداقل یک مقسوم علیه اول است. برای این منظور مجموعه مقسوم علیه های مثبت و بزرگتر از یک a را به این صورت تعریف میکنیم:

مجموعه S ناتهی است چرا که:

پس:
 . از طرفی دیگر مجموعه S زیرمجموعه اعداد طبیعی است پس بنابر اصل خوشترتیبی S دارای عضو ابتدا(مینیمم) چون P است.
. از طرفی دیگر مجموعه S زیرمجموعه اعداد طبیعی است پس بنابر اصل خوشترتیبی S دارای عضو ابتدا(مینیمم) چون P است. 
نشان می دهیم که P عددی اول است. برای اثبات ادعا از برهان خلف استفاده می کنیم:
به برهان خلف فرض می کنیم P عددی اول نباشد، پس P عددی مرکب است لذا:
 ,این نتیجه می دهد:
,این نتیجه می دهد: 
از طرفی دیگر:
 که این نتیجه می دهد:
که این نتیجه می دهد: .
.
و این با مینیمم بودن P در تناقض است چون:
 و لذا فرض خلف باطل و چنین نیست که P اول نباشد پس P اول است. به این ترتیب نشان داده شد عدد a حد اقل یک مقسوم علیه اول دارد.
و لذا فرض خلف باطل و چنین نیست که P اول نباشد پس P اول است. به این ترتیب نشان داده شد عدد a حد اقل یک مقسوم علیه اول دارد.
- قضیه 2) بی نهایت عدد اول وجود دارد.
برای اثبات این قضیه از برهان خلف استفاده می کنیم. به برهان خلف فرض می کنیم تعداد اعداد اول متناهی باشد و به فرض
 تنها اعدد اول موجود باشند. قرار می دهیم:
تنها اعدد اول موجود باشند. قرار می دهیم:

بوضوح M بزرگتر از یک و طبیعی است پس بر طبق قضیه قبل می توان گفت M دارای حداقل یک مقسوم علیه اول است و چون تعداد اعداد اول موجود محدود است آن مقسوم علیه اول یکی از اعداد
 است به فرض عضوی چون:
است به فرض عضوی چون:  داریم:
داریم:

که این با اول بودن
 در تناقض است چون
در تناقض است چون  نه اول و نه مرکب است . و لذل فرض خلف باطل و حکم برقرار است و تعداد اعداد اول بی شمار است.
نه اول و نه مرکب است . و لذل فرض خلف باطل و حکم برقرار است و تعداد اعداد اول بی شمار است.
- لازم به توضیح است که این قضیه نخستین بار توسط اقلیدس در حدود سال 300 قیل از میلاد اثبات گردیده است.
- قضیه 3) هر عدد مرکب n دارای حداقل یک مقسوم علیه اول کوچکتر یا مساوی
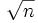 است.
است.
چون n مرکب است پس:

حال نشان می دهیم که:

به برهان خلف اگر:
 آنگاه
آنگاه  و در نتیجه:
و در نتیجه:  که این تناقض است و لذا فرض خلف باطل و حکم برقرار است یعنی:
که این تناقض است و لذا فرض خلف باطل و حکم برقرار است یعنی:  حال چون a بزرگتر از یک است پس a دارای حداقل یک مقسوم علیه اول مانند p است. داریم:
حال چون a بزرگتر از یک است پس a دارای حداقل یک مقسوم علیه اول مانند p است. داریم:

و از سوی دیگر:

پس p عددی اول است که در شرایط قضیه صدق می کند و لذا حکم برقرار است.
- لازم به توضیح است که قضیه فوق اساس روش غربال اراتستن است.
- قضیه4) اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد. (قضیه چپیشف)
- قضیه بنیادی حساب:
به عبارت دیگر اگر n عددی طبیعی و بزرگتر از 1 باشد:

که در آن
 ها اعداد اول متمایر می باشند.
ها اعداد اول متمایر می باشند.
این نمایش را تجزیه عدد n به عوامل اول می گوییم.
همچنین اگر n<-1 باشد باز هم می توان n را به صورت یکتایی به صورت حاصل ضرب عوامل اول نوشت:


که در آن
 ها اعداد اول متمایز می باشند.
ها اعداد اول متمایز می باشند.
- توجه: اگر n=1 باشد آنگاه
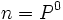 که در ان P هر عدد اولی است.
که در ان P هر عدد اولی است.
- لازم به توضیح است که ممکن است در تجزیه یک عدد طبیعی به عوامل اول، تعدادی از عوامل یکسان باشند. به عنوان مثال:12=2×2×3
اگر n>1 عددی طبیعی باشد آنگاه عدد n را می توان به شکل یکتایی به صورت:

که در آن
 ها اعداد اول متمایز و
ها اعداد اول متمایز و  اعداد طبیعی اند.
اعداد طبیعی اند.
این روش نمایش و تجزیه عدد را تجزیه متعارف، استاندارد، یا کانونیک عدد n می گویند.
به عنوان مثال تجزیه استاندارد 12 به عوامل اول به صورت مقابل است:

مطالب مشابه :
دانلود کتاب ریاضی سوم راهنمایی
دانلود کتاب ریاضی سوم راهنمایی مقطع : راهنمايى پايه : سال سوم آخرين تاريخ بروز رسانى : 1390.
حل تمرینات ریاضی 3 تجربی
آشتی با ریاضی ریاضی راهنمایی و دانلود رایگان کتاب های ریاضی دانشگاهی و
دانلود کتاب ریاضی دوم راهنمایی
بانک سوال ریاضی سوم راهنمایی دانلود کتاب ریاضی دوم راهنمایی سال دوم آخرين
جدول زمانبندی تدریس ریاضی راهنمایی
ریاضی راهنمایی سوم. رسم مثلث حل تمارین و مسائل تا ص 104. ریاضی سال دوم راهنمایی.
روش های حل معادله
اموزش ریاضی سوم راهنمایی وحل تمارین هندسه سال دانلود کتاب حل تمارین ریاضی سوم
فصل اول - بخش سوم : توان
اموزش ریاضی سوم راهنمایی وحل تمارین هندسه سال دانلود کتاب حل تمارین ریاضی سوم
شگفتی های ریاضی در مبحث توان
اموزش ریاضی سوم راهنمایی وحل تمارین هندسه سال دانلود کتاب حل تمارین ریاضی سوم
حل تمرينات و تست هاي كنكور سراسري و آزاد رياضي (1)
اموزش ریاضی سوم راهنمایی وحل تمارین هندسه سال دانلود کتاب حل تمارین ریاضی سوم
عدد اول
اموزش ریاضی سوم راهنمایی وحل تمارین هندسه سال دانلود کتاب حل تمارین ریاضی سوم
برچسب :
تمارین کتاب ریاضی سال سوم راهنمایی