انتگرال

بيش از دو هزار سال پيش ارشميدس (287-212 قبل از ميلاد) فرمول هايي را براي محاسبه سطح وجه ها ، ناحيه ها و حجم هاي جامد مثل كره ، مخروط و سهمي يافت . روش انتگرال گيري ارشميدس استثنايي و فوق العاده بود جبر ، نقش هاي بنيادي ، كليات و حتي واحد اعشار را هم نمي دانست .
ليبنيز (1716-1646) و نيوتن (1727-1642) حسابان را كشف كردند . عقيده كليدي آنها اين بود كه مشتق گيري و انتگرال گيري اثر يكديگر را خنثي مي كنند با استفاده از اين ارتباط ها آنها توانستند تعدادي از مسائل مهم در رياضي ، فيزيك و نجوم را حل كنند.فورير (1830-1768) در مورد رسانش گرما بوسيله سلسله زمان هاي مثلثاتي را مي خواند تا نقش هاي بنيادي را نشان دهد .رشته هاي فورير و جابجايي انتگرال امروزه در زمينه هاي مختلفي چون داروسازي و موزيك اجرا مي شود .
گائوس (1855-1777) اولين جدول انتگرال را نوشت و همراه ديگران سعي در عملي كردن انتگرال در رياضي و علوم فيزيك كرد . كايوچي (1857-1789) انتگرال را در يك دامنه همبستگي تعريف كرد . ريمان (1866-1826) و ليبيزگو (1941-1875) انتگرال معين را بر اساس يافته هاي مستدل و منطقي استوار كردند .
ليوويل (1882-1809) يك اسكلت محكم براي انتگرال گيري بوجود آورد بوسيله فهميدن اينكه چه زماني انتگرال نامعين از نقش هاي اساسي دوباره در مرحله جديد خود نقش اساسي مرحله بعد هستند . هرميت (1901-1822) يك شيوه علمي براي انتگرال گيري به صورت عقلي و فكري ( يك روش علمي براي انتگرال گيري سريع ) در دهه 1940 بعد از ميلاد استراسكي اين روش را همراه لگاريتم توسعه بخشيد .
در دهه بيستم ميلادي قبل از بوجود آمدن كامپيوترها رياضيدانان تئوري انتگرال گيري و عملي كردن آن روي جداول انتگرال را توسعه داده بودند و پيشرفت هايي حاصل شده بود .در ميان اين رياضيدانان كساني چون واتسون ، تيچمارش ، بارنر ، ملين ، ميچر ، گرانبر ، هوفريتر ، اردلي ، لوئين ، ليوك ، مگنوس ، آپل بلت ، ابرتينگر ، گرادشتاين ، اكستون ، سريواستاوا ، پرودنيكف ، برايچيكف و ماريچيف حضور داشتند .
در سال 1969 رايسيچ پيشرفت بزرگي در زمينه روش علمي گرفتن انتگرال نامعين حاصل كرد . او كارش را بر پايه تئوري عمومي و تجربي انتگرال گيري با قوانين بنيادي منتشر كرد روش او عملاً در همه گروه هاي قضيه بنيادي كارگر نيست تا زماني كه در وجود آن يك معادله سخت مشتق گيري هست كه نياز دارد تا حل شود . تمام تلاش ها ااز آن پس بر روي حل اين معادله با روش علمي براي موفقيت هاي مختلف قضيه اساسي گذاشته شد . ايت تلاش ها باعث پيشرفت كامل سير و روش علمي رايسيچ شد . در دهه 1980 پيشرفت هايي نيز براي توسعه روش او در موارد خاص از قضيه هاي مخصوص و اصلي او شد .
از قابليت تعريف انتگرال معين به نتايجي دست ميابيم كه نشان دهنده قدرتي است كه در رياضيات مي باشد (1988) جامعيت و بزرگي به ما ديدگاه موثر و قوي در مورد گسترش در رياضيات و همچنين كارهاي انجام شده در قوانين انتگرال مي دهد . گذشته از اين رياضيات توانايي دارد تا به تعداد زيادي از نتيجه هاي مجموعه هاي مشهور انتگرال پاسخ دهد ( اينكه بفهميم اين اشتباهات ناشي از غلط هاي چاپي بوده است يا نه ) . رياضيات اين را ممكن مي سازد تا هزاران مسئله انتگرال را حل نماييم به طوريكه تا كنون در هيچ يك از كتابهاي دستنويس قبلي نيامده باشد . در آينده ديگر وظيفه ضروري انتگرال اين است كه به ازمايش تقارب خطوط ، ارزش اصلي آن و مكانيسم فرض ها بپردازد .

انتگرالها یک بحث اساسی ریاضیات عالی را تشکیل داده که میتوان کاربرد آنرا درتمام علوم طبیعی، انسانی وغیره مورد مطالعه قرارداد.

اولین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد. 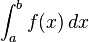$\int_{a}^{b} f(x)\, dx$ aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.

از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می‌دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است.

تابع اولیه

هر گاه معادله مشتق تابعی معلوم باشد وبخواهیم معادله اصلی تابع را تعیین کنیم این عمل را تابع اولیه می نامیم.

تعریف: تابع اولیه y = f(x)را تابعی مانند Y = F(x) + c می نامیم،هرگاه داشته باشیم:

cعدد ثابت (y = F(x) + c)' = y = f(x)

انتگرال نامعین

تعریف:هرگاه معادله دیفرانسیلی تابعی معلوم باشد وبخواهیم معادله اصلی تابع را معلوم کنیم این عمل راانتگرال نا معیین نامیده و آن را با نماد $\int$ نمایش می دهند.

بنا به تعریف نماد $\int{f(x)}.dx$ را انتگرال نامعین نامیده وحاصل آن را تابعی مانندF(x) + c در نظر میگیریم هر گاه داشته باشیم: $\int{f(x)}.dx=F(x)+c$ با شرط: (F(x) + c)' = f(x)

انتگرال معین

بنا به تعریف نماد $\int_a^b f(x).dx$ را انتگرال معین نامیده و حاصل آن را عددی به صورت زیر تعریف میکنیم: a

aوb را به ترتیب کرانهای بالا و پایین انتگرال مینامیم.

تابع انتگرال‌پذیر

اگر تابعی دارای انتگرال باشد به آن انتگرال‌پذیر گویند.

تعبیر هندسی انتگرال

از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.

نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سه‌گانه معرف پارالل زیر نمودار است(غیرقابل تصور).

مثال

انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی fx است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.
انتگرال یک تابع مساحت زیر نمودار آن تابع است.

انتگرال گیری

(محاسبه ي انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است.

مهم‌ترین تعاریف در انتگرال

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال 1854 ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعويض پذيری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان-استیلچس (Riemann-Stieltjes) اشاره کرد. پس به طور خلاصه سه تعریف زير از مهم‌ترين تعاريف انتگرال مي باشند:

- انتگرال ريمان
- انتگرال لبگ
- انتگرال ريمان-استيلتيس (تعميم انتگرال ريمان)

انتگرال ريمان
در شاخه‌ای از ریاضیات به نام آنالیز حقیقی، ‫برنهارت ‫ریمان انتگرال ریمان، که اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته می‌شود، را ارائه داد. گرچه انتگرال ریمان دارای محدودیت‌هایی برای بسیاری از مسائل تئوری است، ولی یکی از ساده‌ترین روش‌های تعریف انتگرال بوده و بطور گسترده‌ای بکار می‌رود.

(دنباله‌ای از مجموع ریمان. عدد نمایش داده شده در بالای شکل، سمت راست، برابر با مجموع مساحت مستطیل‌های خاکستری است. این مجموع به مقدار انتگرال تابع میل می‌کند.)

کاربرد انتگرال

انتگرال ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می توان برای کاربرد های زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترموديناميكي از انتگرال رابطه فشار و حجم به دست می آید. اما به طور کلی می توان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیت ها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته می شود:

$v=[L]/[T] t=[T] \!$

سپس دو تحلیل را در هم ضرب می کنیم:

$[L] \!$

پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.

محاسبه ي انتگرال
اکثر روش های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:

1.f تابعی در بازه (a,b) در نظر می‌‌گیریم. 2.پاد مشتق f را پیدا می‌‌کنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می‌‌گیریم،
بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می‌‌دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار ساده‌ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارت‌اند از :

- انتگرال گیری به‌وسیله تغییر متغیر
- انتگرال گیری جزء به جزء : $\int u\, dv=uv - \int v\, du$
- انتگرال گیری با تغییر متغیر مثلثاتی
- انتگرال گیری به‌وسیله تجزیه کسرها

روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می‌‌رود همچنین می‌‌توان بعضی از انتگرال ها با ترفند هایی حل کرد برای مثال می‌‌توانید به انتگرال گاوسی مراجعه کنید.

تقریب انتگرالهای معین

محاسبه سطح زیر نمودار به‌وسیله مستطیل هایی زیر نمودار. هر چه قدرعرض مستطیل ها کوچک می‌شوندمقدار دقیق تری از مقدار انتگرال بدست میآید.
انتگرال هایی معین ممکن است با استفاده از روش های انتگرال گیری عددی ،تخمین زده شوند.یکی از عمومی‌ترین روش ها ،روش مستطیلی نامیده می‌‌شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه‌ای است. اگر چه روش های عددی مقدار دقیق انتگرال را به ما نمی‌دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می‌‌کند.

انتگرال چند گانه
انتگرال چندگانه نوعی از انتگرال است که برای بدست آوردن حجم یا پارالل زیر تابع‌های بیش از یک متغییر استفاده می شود.

(انتگرال دوگانه برای بدست آوردن حجم محصور در زیر توابعی به کار می رود که دو متغییر دارند.)

روش نمایش

توابع با بیش از یک متغییر را با $\;f(x_1,x_2,\ldots,x_n)$ یا $\;f(x,y,z,t)$ نمایش می دهند.

و روش نمایش انتگرال چندگانه به صورت زیر است:

$\iint \ldots \int_\mathbf{D}\;f(x_1,x_2,\ldots,x_n) \;\mathbf{d}x_1 \mathbf{d}x_2\!\ldots\mathbf{d}x_n$

انتگرال‌های چندگانه

انتگرال دوگانه:معرف حجم زیر تابع است که دو متغییر دارد. مثلا:

$\iint f(x,y) \ dx\, dy$

انتگرال سه گانه:معرف پارالل زیر نمودار(می توان آن را نوعی حجم ضربدر زمان گرفت) است مثلا: $\iiint_\mathrm{parallelepiped} f(x,y,z) \, dx\, dy\, dz$

تبدیل انتگرال چندگانه به انتگرال خطی
برای انواع مختلف تابع این روش متفاوت می باشد ولی راحترینش برای توابع مستطیلی(توابعی سه بعدی که x و y آنها به هم ارتباط نداشته باشد)است که به راحتی اول از این تابع یک انتگرال خطی برحسب یکی از متغییرها گرفته می شود و سپس از تابع دوم(که دارای یکی دیگر از متغییرهاست)برحسب متغییر دوم انتگرال خطی گرفته می شود.

اما برای توابعی که مستطیلی نیستند از نظریه‌های متفاوتی استفاده می شود منجمله :نظریه دیورژانس٬نظریه سبز و ...

-----------------------
پيوست: حل انتگرال بصورت آنلاين:
www.integrals.wolfram.com/index.jsp

منبع: دانشنامه ويكي پديا
www.wikipedia.org
www.en.wikipedia.org
اين مقاله، بصورت گروهي تحقيق شده است

انتگرال

مطالب مشابه :

انتگرال ریمان

انتگرال ریمان

انتگرال ریمان

انتگرال

اندازه و انتگرال لبگ

انتگرال

انتگرال و دعوای نیوتن و لایب نیتز

برنهارد ریمان

انالیز ریاضی

برنهارد ریمان