گام تصادفی (Random walk)

تست‌های اولیه در مورد کارایی بازار، عموماً مبتنی بر آزمون «گام تصادفی» بودن حرکت قیمت‌های سهام بود. ردشدن مدل گام تصادفی دلیلی بر عدم‌کارایی بازار تلقی می‌شد؛ بنابراین وجود هرگونه الگویی برای پیش‌بینی بازده سهام نشانگر نقض فرضیه بازار کارا بود.

مدل‌های گام تصادفی پس از ارائه نظریه بازار کارا توسط فاما توسعه یافتند. فرض صفر چنین آزمون‌هایی وجود یکی از انواع گام تصادفی در حرکت قیمت‌هاست. کمپل، لو و مک‌کنلی (١٩٩٧) (Campbell, Lo, Mackinlay) انواع مدل‌های گام تصادفی ارائه‌شده را به‌همراه ویژگی‌های هریک جمع‌آوری کردند. یک مدل پایه گام تصادفی به صورت زیر است:

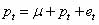
که در آن Pt قیمت دارایی در زمان بازده مورد انتظار، و فرضیات در مورد et در انواع مدل‌های گام تصادفی متفاوت می‌باشد. در میان مدل‌های گام تصادفی مدل RW1 محدودترین مدل است (یعنی بیشترین قیدها را به مدل تحمیل می‌کند)، و مدل‌های RW2 و RW3 به ترتیب محدودیت‌های کمتری روی مدل اعمال می‌کنند. در ادامه انواع مدل‌های گام تصادفی به‌طور اجمالی معرفی خواهد شد.

مدل گام تصادفی نوع ١

مدل گام تصادفی نوع ١ ساده‌ترین نوع گام تصادفی است که پسماندها را مستقل و دارای توزیع یکسان (i.i.d) در نظر می‌گیرد. دینامیک بازده در این مدل به‌صورت زیر می‌باشد:

در این مدل پسماندها مستقل از هم و با توزیع یکسان فرض شده‌اند، لذا مدل واریانس ناهمسانی (تغییرات تلاطم در طول زمان) و ویژگی خوشه‌ای بودن تلاطم (وجود همبستگی در تلاطم) بازده را نمی‌تواند توضیح دهد. استقلال پسماندها بدین معناست که نه تنها پسماندها همبستگی ندارند، بلکه هر تابع غیرخطی از پسماندها نیز ناهمبسته هستند.

چنان‌چه تلاطم بازده‌ها در طول زمان تغییرات قابل‌توجهی داشته باشد، فرضیه گام تصادفی با انجام آزمون مربوطه رد خواهد شد؛ اما، این مطلب (رد فرضیه گام تصادفی ١) ممکن است اطلاعاتی در خصوص پیش‌بینی‌پذیری بازده به ما ندهد. وجود هرگونه خودهمبستگی معنادار آماری در بازده‌ها و توان دوم بازده‌ها این فرضیه را رد خواهد کرد. با توجه به ویژگی‌های معمول سری‌های زمانی بازده، فروض این مدل بسیار قوی بوده و با دنیای واقعی، به‌ویژه در دوره‌های بلندمدت چندان سازگار نیست.

مدل گام تصادفی ٢

یک مدل ساده گام تصادفی نوع ٢ به‌صورت زیر است:

بنابراین مقدار انتظاری شرطی بازده در تمامی دوره‌ها یکسان خواهد بود، ضمن این‌که بازده‌ها از یکدیگر مستقل فرض شده‌اند، لذا هیچ‌یک از گشتاورهای بازده همبستگی ندارند. این مدل فرض یکسان بودن توزیع پسماندها را حذف می‌کند؛ بنابراین، امکان توضیح واریانس ناهمسانی را دارد. لکن، همچنان فرض قوی مستقل بودن پسماندها پابرجاست؛ لذا، ویژگی خوشه‌ای بودن تلاطم بازده را نمی‌تواند توضیح دهد. آزمون RW2 بسیار دشوار است. زیرا تست استقلال پسماندها در حین پذیرفتن امکان توزیع‌های متفاوت برای پسماندها پیچیده می‌باشد.

مدل گام تصادفی ٣

بالاخره یک مدل ساده گام تصادفی نوع ٣ به‌صورت زیر می‌باشد:

این مدل کم‌ترین محدودیت را نسبت به مدل‌های قبلی گام تصادفی دارد، چرا که علاوه بر امکان وجود توزیع‌های مختلف برای پسماندها، فرض مستقل بودن پسماندها را نیز حذف می‌کند و به‌جای آن پسماندهای را تنها ناهمبسته فرض می‌کند. یعنی گشتاور اول پسماندها ناهمبسته فرض می‌شود؛ اما، گشتاورهای بالاتر بازده می‌توانند همبستگی داشته باشند. لذا، این مدل امکان توضیح واریانس ناهمسانی و ویژگی خوشه‌ای بودن تلاطم بازده را دارد.

این مدل کمترین قیدها را دارد و آزمون آن نسبت به دیگر مدل‌های گام تصادفی این مدل آزمون می‌شود. مدل‌های گام تصادفی همراه با ویژگی‌ها و روش‌های آزمون هریک در جدول زیر خلاصه شده است. در این تحقیق به‌منظور آزمون گام تصادفی نوع اول، آزمون ناپارامتری تسلسل‌ها و برگشت‌ها (Sequences and reversals) و برای آزمون خودهمبستگی بازده و تلاطم، آزمون‌های باکس-پریس (Box-Pierce) و نسبت واریانس (Variance ratio) استفاده شده است. این آزمون‌ها در فصل ٥ توضیح داده شده‌اند.

جدول ٢-١) مدل‌های گام تصادفی، ویژگی‌ها و روش‌های آزمون

گام تصادفی (Random walk)

مطالب مشابه :

مدل های تعادل عمومی پویای تصادفی - DSGE

++C تولید اعداد تصادفی در

ادامه تکنیک های خلاقیت

گام تصادفی (Random walk)

پژو 206 مدل 81 دور رنگ بیمه برج 12 موتور( روغن سوزی دارد) قیمت 9 م