ماتریسها
| در ریاضیات ماتریس عبارت است یک جدول مستطیلی از اعداد و یا به صورت ساخت یافتهتر: ماتریس مجموعهای از اشیای هم نوع است که به تعدادی گروه با اعضای یکسان تقسیم بندی شده است. ماتریسها ریاضیات مناسبی برای ثبت و ذخیره دادههایی هستند که مقادیر آنها به دو کمیت بستگی دارد. از این جهت چون در اکثر علوم با چنین دادههایی روبرو میشویم. بنابراین کاربرد وسیع ماتریسها در اکثر شاخههای علوم مهندسی میشود. |
ماتریس
ماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر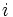 ام و ستون
ام و ستون  ام را با نماد
ام را با نماد  نشان میدهیم.
نشان میدهیم. ماتریسی که دارای
 سطر و
سطر و  ستون باشد را ماتریس از مرتبه
ستون باشد را ماتریس از مرتبه  در
در  مینامیم.(
مینامیم.(  )
) نکته
هرگاه آنگاه ماتریس را مربع از مرتبه
آنگاه ماتریس را مربع از مرتبه  مینامیم.
مینامیم. یک ماتریس
 را بصورت
را بصورت  نمایش میدهیم.
نمایش میدهیم. تاریخچه
مطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد.در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر اساس استفاده صریح از دترمینان ماتریس ضرایب معرفی گردیده است. در مقابل اولین استفاده ضمنی از ماتریسها توسط لاگرانژ برای تعیین ماکزیمم و مینیمم توابع چند مقداری مورد استفاده قرار گرفت. در ادامه گاوس روش حذفی خود را برای حل مسائل کمترین مربعات که کاربردهای بسیار وسیعی در علوم سماوی و ژئودوزی دارد را معرفی کرد.
روابط بین ماتریسها
تساوی دو ماتریس
دو ماتریس و
و مساوی اند اگر و فقط اگر
مساوی اند اگر و فقط اگر  (هم مرتبه باشند) و
(هم مرتبه باشند) و
جمع دو ماتریس
اگر و
و آنگاه
آنگاه 
قرینه ماتریس
اگر آنگاه قرینه
آنگاه قرینه  را بصورت زیر تعریف میکنیم:
را بصورت زیر تعریف میکنیم: 
ضرب اسکالر در ماتریس
اگر و
و یک اسکالر باشد آنگاه
یک اسکالر باشد آنگاه
در ضرب اسکالر یک عدد در یک ماتریس ضرب میشود. در این نوع ضرب تمامی عناصر ماتریس در آن عدد ضرب میشوند به عنوان مثال:
و نمایش ریاضی آن به صورت زیر می باشد:
cA)ij = c(A)ij)
ضرب ماتریسها
اگر و
و  آنگاه ضرب دو ماتریس را با علامت
آنگاه ضرب دو ماتریس را با علامت  نمایش داده و بصورت زیر تعریف خواهیم کرد:
نمایش داده و بصورت زیر تعریف خواهیم کرد: 
در این نوع هر دو ضرب شونده و ضرب کننده از نوع ماتریس میباشند. بطور مشابه ضرب دو ماتریس نیز باید یک جنبه خوش تعریفی داشته باشد. ضرب دو ماتریس داده شده A و B زمانی خوش تعریف است که تعداد ستونهای ماتریس ضرب کننده با تعداد سطرهای ماتریس ضرب شونده برابر باشند. بر این ضرب دو ماتریس که شرایط قابل ضرب بودن را داشته باشند به صورت زیر بیان میشود:
برای بدست آوردن عنصر روی سطر iام و ستون y ام ماتریس خاصل ضرب عناصر روی سطر iام ماتریس ضرب کننده و عناصر روی ستون j ام ماتریس ضرب شونده را در نظر گرفته و آنها در هم ضرب و جمع می کنیم. به صورت ریاضی حاصلضرب دو ماتریس بصورت زیر نمایش داده می شود:
A × B)ij = (A)i1(B)1j + (A)i2(B)2j + ... + (A)in(B)nj)
بطور سادهتر میتوان ماتریس ضرب کننده را به صورت مجموعه ای از بردارهای نظری و ماتریس ضرب شونده را به صورت مجموعهای بردارهای ستونی در نظر گرفت.
انواع ماتریس
ماتریس صفر
ماتریسی که تمام درایه های آن صفر باشد را ماتریس صفر نامیده و ماتریس صفر از مرتبه را با نماد
را با نماد  نمایش میدهیم و داریم
نمایش میدهیم و داریم 
ماتریس همانی
ماتریس مربع از مرتبه
از مرتبه  را همانی گوییم هرگاه
را همانی گوییم هرگاه وبه ازای هر
وبه ازای هر  داشته باشیم
داشته باشیم 
ماتریس اسکالر
اگر یک اسکالر و
یک اسکالر و  ماتریس همانی از مرتبه
ماتریس همانی از مرتبه باشد آنگاه
باشد آنگاه  را ماتریس اسکالر مینامیم.
را ماتریس اسکالر مینامیم. ماتریس وارون پذیر
ماتریس مربع را وارون پذیر مینامیم هرگاه ماتریس مربع
را وارون پذیر مینامیم هرگاه ماتریس مربع  یافت شود به طوری که
یافت شود به طوری که  .دراین صورت
.دراین صورت  را وارون
را وارون  مینامیم.
مینامیم. ماتریس قطری
ماتریس مربعی را قطری نامیم هرگاه عناصر روی قطر اصلی همگی غیر صفر باشند و عناصر غیر از قطر اصلی صفر باشند.
را قطری نامیم هرگاه عناصر روی قطر اصلی همگی غیر صفر باشند و عناصر غیر از قطر اصلی صفر باشند. چند خاصیت از ماتریس ها
اگر سه ماتریس
سه ماتریس  و
و دو اسکالر باشند آنگاه:
دو اسکالر باشند آنگاه: 







اگر
 آنگاه
آنگاه 
اگر
 آنگاه
آنگاه 
اگر
 انگاه
انگاه 
در حالت کلی ضرب ماتریسها خاصیت جابجایی ندارد.(حتی اگر
 تعریف شده باشند و این در حالتی ممکن است که
تعریف شده باشند و این در حالتی ممکن است که دو مربع هم مرتبه باشند.)
دو مربع هم مرتبه باشند.)
انواع ماتریسها
ماتریس مربعی
ماتریسی است که تعداد سطرها و ستونهای آن با هم برابر باشد.
ماتریس سطری
ماتریسی است که یک سطر دارد. مثلا

ماتریس ستونی
ماتریسی است که یک ستون دارد. مثلا

ماتریس 
ماتریسی است که فقط یک عضو دارد. مثلا

ماتریس صفر
تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است.

ماتریس واحد یا یکه
ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر میباشد. این ماتریس را با I نشان میدهند. مثلا

!ماتریس قرینه
اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند.
ماتریس قطری
ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا

ماتریس عددی یا اسکالر
ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا

ماتریس منفرد
ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی 
ماتریس غیرمنفرد یا وارونپذیر
اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد میگویند. یعنی 
ماتریس معکوس یا ماتریس وارون
ماتریس مربعی A را در نظر میگیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A میگویند معمولا ماتریس معکوس A را بصورت  نشان میدهند و در نتیجه داریم:
نشان میدهند و در نتیجه داریم:

ماتریس همسازه
اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست میآید که به آن همسازه میگویند. ماتریس همسازه A را با N نمایش میدهند.

برای هر  در ماتریس
در ماتریس  ، همسازه
، همسازه  برابر است با عدد
برابر است با عدد
کوفاکتور عضو 

بطوریکه ،  را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد.
را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد.
ماتریس وابسته یا الحاقی
به ترانسپوزه ماتریس همسازه A ماتریس وابسته A میگویند و آن را با  نشان میدهند.
نشان میدهند.
ماتریس متقارن
اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن مینامند بعبارت دیگر ماتریس A متقارن است در صورتیکه  باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند.
باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند.
ماتریس ضدمتقارن یا آنتیمتقارن
هرگاه قرینه ترانسپوزه ماتریس A برابر A شود، به آن ماتریس ضدمتقارن میگویند و داریم 
ماتریس پایین مثلثی
اگر در یک ماتریس مربعی تمام عضوهای بالای قطر اصلی صفر باشند به آن ماتریس پایین مثلثی میگویند یعنی 
ماتریس بالا مثلثی
اگر در یک ماتریس مربعی تمام عضوهای پایین قطر اصلی صفر باشند به آن ماتریس بالا مثلثی میگویند. یعنی
ماتریس متعامد
اگر در ماتریس مربعی A داشته باشیم  به ماتریس متعامد میگویند
به ماتریس متعامد میگویند
دترمینان
به هر ماتریس مربع از مرتبه  مانند
مانند میتوان عددی را نسبت داد.این عدد را با نماد
میتوان عددی را نسبت داد.این عدد را با نماد  یا
یا  نمایش میدهیم و آن را دترمینان
نمایش میدهیم و آن را دترمینان  میخوانیم.
میخوانیم.
اگر :

آنگاه:

خواص دترمینان
اگر ستونهای ماتریس را با
را با  نشان دهیم آنگاه
نشان دهیم آنگاه  و خواهیم داشت :
و خواهیم داشت : 








تعریف
اگر یک ماتریس مربع از مرتبه
یک ماتریس مربع از مرتبه  باشد آنگاه ماتریس حاصل از حذف سطر
باشد آنگاه ماتریس حاصل از حذف سطر 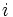 ام و ستون
ام و ستون  ام که یک ماتریس از مرتبه
ام که یک ماتریس از مرتبه  در
در  است را با نماد
است را با نماد  نمایش میدهیم.در اینصورت:
نمایش میدهیم.در اینصورت: 
قضیه1
اگر دو ماتریس باشند آنگاه:
دو ماتریس باشند آنگاه: قضیه2
اگریک ستون از ماتریس مربع از مرتبه
از مرتبه  مضربی از ستون دیگر آن باشد آنگاه
مضربی از ستون دیگر آن باشد آنگاه
اثبات:

بنابراین:

لذا:

---
قضیه3

اثبات:
به استقرا روی عمل میکنیم:
عمل میکنیم:

فرض استقرا:

حکم استقرا:

اما:

مطالب مشابه :
جزوه ماتریس
هدف از ایجاد وبلاگ دسترسی دانش آموزان و دانشجویان به نمره هایشان و جزوه ها ی مختلف و موضوعات
جزوه درس ریاضیات کاربردی
جزوه درس ریاضیات معکوس ماتریس. دستگاه معادلات
دانلودجزوه ریاضیات کاربردی
دانلودجزوه ریاضیات کاربردی این جزوه شامل سرفصل های زیرمی باشد: جزوه ماتریس ها
دانلود جزوه آموزشی ریاضی سال دوم دبیرستان مبحث ماتریس
دانلود جزوه آموزشی ریاضی سال دوم دبیرستان مبحث ماتریس. لینک مستقیم : جزوه آموزشی ریاضی سال
ماتریسها
ماتریس عبارت است از ایجاد وبلاگ دسترسی دانش آموزان و دانشجویان به نمره هایشان و جزوه ها ی
تانسورها
دانلود کتاب و جزوه ریاضی (در بحث ماتریس ها، یک ماتریس عمومی از جمع دو ماتریس پادمتقارن و
ماتریس : نظریه و کاربردها
گروه ریاضی دانشگاه پیام نور - ماتریس : دانلود جزوه جبر پیشرفته- مقطع کارشناسی
تست ماتریس
ریاضی - تست جزوه مطلب ریاضی نوشته شده توسط بختياري در شنبه بیست و پنجم آذر ۱۳۹۱ و ساعت 23:45 |
کتاب درس مبانی ماتریسها و جبر خطی
کتاب مبانی ماتریس ها و جبرخطی به نویسندگی بیژن زاده ، فرهمند ، چایچی . کتابها و جزوه های
دانلود جزوه هندسه تحلیلی مبحث ماتریس و دستگاه
دانلود جزوه هندسه تحلیلی مبحث ماتریس و دستگاه کاری از استاد محبی پور شامل درسنامه های جامع
برچسب :
جزوه ماتریس




