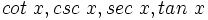توابع مثلثاتی معکوس
منشا توابع مثلثاتی معکوس، مسائلی است که در آن ها باید با استفاده از اندازه ی اضلاع یک مثلث، زوایای آن را به دست آورد. این توابع، پاد مشتق بسیاری از توابع دیگر هم هستند و لذا در جواب های تعدادی از معادلات دیفرانسیل مورد بحث در ریاضیات، مهندسی و فیزیک ظاهر میشوند.
آرک سینوس
تابع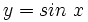 یک به یک نیست؛ این تابع در بازه های به طول
یک به یک نیست؛ این تابع در بازه های به طول  ، دو بار سراسر برد مقادیرش، یعنی از
، دو بار سراسر برد مقادیرش، یعنی از  تا
تا  را طی می کند. ولی اگر دامنه ی سینوس را به بازه ی
را طی می کند. ولی اگر دامنه ی سینوس را به بازه ی  محدود کنیم، آن گاه تابع محدود شده ی
محدود کنیم، آن گاه تابع محدود شده ی  یک به یک و بنابر این دارای معکوسی است که با
یک به یک و بنابر این دارای معکوسی است که با  نمایش داده می شود و غالبا به صورت
نمایش داده می شود و غالبا به صورت  نوشته می شود.
نوشته می شود. با توجه به شکل1، اگر
 ، آن گاه
، آن گاه  آرکی (قوسی) از دایره ی واحد است که سینوسش
آرکی (قوسی) از دایره ی واحد است که سینوسش  می باشد. پس به ازای هر مقدار
می باشد. پس به ازای هر مقدار  در بازه ی
در بازه ی  ،
،  عددی از بازه ی
عددی از بازه ی  است که سینوس آن
است که سینوس آن  خواهد بود.
خواهد بود. 
توجه:نمودار آرک سینوس نسبت به مبدا متقارن است زیرا که نمودار
 نسبت به مبدا متقارن می باشد. از نظر جبری، این بدین معناست که به ازای هر
نسبت به مبدا متقارن می باشد. از نظر جبری، این بدین معناست که به ازای هر  در دامنه ی آرک سینوس:
در دامنه ی آرک سینوس:  که راه دیگری است برای بیان فرد بودن تابع
که راه دیگری است برای بیان فرد بودن تابع  .
. آرک کسینوس
تابع کسینوسی هم نظیر تابع سینوسی یک به یک نیست، اما اگر به بازه ی
هم نظیر تابع سینوسی یک به یک نیست، اما اگر به بازه ی  محدود شود یک به یک خواهد بود و معکوسی دارد که به آرک کسینوس
محدود شود یک به یک خواهد بود و معکوسی دارد که به آرک کسینوس  معروف است. به ازای هر مقدار
معروف است. به ازای هر مقدار  در بازه ی
در بازه ی  ،
،  عددی از بازه ی
عددی از بازه ی  می باشد که کسینوس آن
می باشد که کسینوس آن  است.
است. 
همان طور که در شکل2 ملاحظه می کنید، آرک کسینوس
 در اتحاد
در اتحاد 
یا

صدق می کند و با توجه به مثلث شکل3 نیز دیده می شود که به ازای
 :
: 
زیرا در این صورت
 و
و  زوایای متمم در یک مثلث قایم الزاویه اند که طول وترش یک واحد و طول یکی از ساق هایش
زوایای متمم در یک مثلث قایم الزاویه اند که طول وترش یک واحد و طول یکی از ساق هایش  واحد است.
واحد است. 
نکته: به سادگی ثابت می شود که اتحاد
 به ازای سایر مقادیر
به ازای سایر مقادیر  واقع در
واقع در  هم برقرار است.
هم برقرار است. معکوس 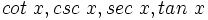
چهار تابع مثلثاتی اساسی دیگر  ،
،  ،
،  و
و  هم، وقتی به طور مناسبی محدود شوند، معکوس دارند.
هم، وقتی به طور مناسبی محدود شوند، معکوس دارند. معکوس
 یا
یا  نمایش داده می شود . دامنه ی آرک تانژانت تمام اعداد حقیقی است و بردش، بازه ی باز
نمایش داده می شود . دامنه ی آرک تانژانت تمام اعداد حقیقی است و بردش، بازه ی باز است. به ازای هر مقدار
است. به ازای هر مقدار  ،
،  زاویه ای است بین
زاویه ای است بین  و
و  و تانژانت آن
و تانژانت آن  است.
است. نمودار
 نسبت به مبدا متقارن است زیرا شاخه ای است از نمودار
نسبت به مبدا متقارن است زیرا شاخه ای است از نمودار  که نسبت به مبدا متقارن است. از نظر جبری، این بدین معناست که:
که نسبت به مبدا متقارن است. از نظر جبری، این بدین معناست که: . آرک تانژانت هم نظیر آرک سینوس تابع فردی از
. آرک تانژانت هم نظیر آرک سینوس تابع فردی از است.
است. معکوس های توابع (محدود شده):



چنان انتخاب شده اند که در روابط زیر صدق کنند:



مطالب مشابه :
در این مقاله روشی برای محاسبه ی سینوس زوایای دلخواه ارائه می شود كه به كمك آن
در این مقاله روشی برای محاسبه ی سینوس زوایای های مثلثاتی را اندازه ی خودش تا
توابع مثلثاتی معکوس
منشا توابع مثلثاتی معکوس، مسائلی است که در آن ها باید با استفاده از اندازه ی زوایای متمم
مثلث
ریاضیات دوره ی مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای نسبت های مثلثاتی
مثلث
مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای مثلثاتی مانند sin و اندازه زاویه
جدول مثلثاتی
این وب تقدیم به روح آســمانی پدرم و همه ی پدرانی که یادشان پرچم صلحی ست به جدول مثلثاتی.
زاویه و دایره
کاربرد تکنیک های حافظه برای حفظ سریع فرمول های ریاضی و مثلثاتی اندازه ی زوایای داخلی
روش محاسبه سطح مثلث و اشکال هندسی
مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای نسبت های مثلثاتی قاعده ی منشور
زاویه و دایره
نرم افزار در زمینه رسم معادلات خطی ، توابع مثلثاتی اندازه ی 3 نیمساز زوایای
مثلث قائم الزاویه و روابط مثلثاتی
به حسب درجه، گراد رادیان اندازه مثلثاتی که برای زوایای مختلف دوره ی راهنمایی
برچسب :
اندازه ی زوایای مثلثاتی