اموزش متلب_pdepe(حل عددی معادله حرارت پاره ای وابسته به زمان)

امروز قراره معادلات گرمایی در فضای تک بعد رو با چند مثال بررسی کنیم. برای حل معادله گرما در زمان t و در فضای تک بعدی از دستور pdepe استفاده می کنیم.
فرم کلی معادله سھمی وار متلب بصورت زیر می باشد.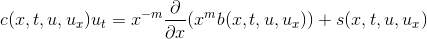

$gif.latex?c(x,t,u,u_{x})u_{t}=x^{-m}%20\$
و ھمین طور فرم کلی شرایط مرزی بصورت زیر می باشد.

$gif.latex?p(x_{l},t,u)+q(x_{l},t).b(x_{l$ $gif.latex?p(x_{r},t,u)+q(x_{r},t).b(x_{r$
که xl نمایانگر نقطه ابتدا و xr نمایانگر نقطه انتهایی شرایط مرزی می باشد.توجه کنید که b دارای مقدار ثابت در هر دو معادله است.هر کدام از معادله های بالا را در m.file جداگانه قرار می دهیم.مقادیر s,b,c را از مقایسه معادله حاکم در مثال با فرم کلی معادله سهمیگون در متلب بدست اورده و در m.file قرار می دهیم.مقادیر p,q را نیز از مقایسه شرایط مرزی مسئله با فرم کلی شرایط مرزی تعریف شده برای متلب بدست می اوریم.و در اخر نیز شرایط کرانه ای را در m.file سوم قرار می دهیم.سپس به کمک دستور pdepe سه m.file را ترکیب کرده معادله را حل می کنیم.
:Exampleمعادله اصلی بصورت:
$gif.latex?u_{t}=u_{xx}$ شرایط مرزی بصورت:
$gif.latex?\dpi{100}%20u(t,1)=1$ $gif.latex?\dpi{100}%20u(t,0)=0$ و شرایط اولیه بصورت:
$gif.latex?\dpi{100}%20u(0,x)=\frac{2x}{1$
کاملا مشخص است که مقدار c=1 می باشد.همچنین ما در طرف راست معادله حاکم بر مسئله مشتق دوم بر حسب x را داریم.پس مقدار b باید برابر ux باشد.مقدار s نیز که به وضوح مشخص است که برابر 0 می باشد. ملاحضه کردید که مقادیر c,b,s طوری در معادله سهمیگون مقدار دهی شدند که به معادله حاکم بر مسئله برسیم.مقدار m نیز باید برابر 0 باشد تا عملا x از معادله حذف شود. m را در اخر مقدار دهی میکنیم.
کد زیر نمایانگر معادله اصلی و در eqn1.m ذخیره می کنیم.

function [c,b,s] = eqn1(x,t,u,DuDx)%EQN1: MATLAB function M-file that specifies%a PDE in time and one space dimension.c = 1;b = DuDx;s = 0;

برای شرایط مرزی نیز مطابق معادله اصلی عمل می کنیم. برنامه نویسان شرایط مرزی را بگونه ای به فرم بالا در اورده اند تا برای تمامی معادلات عمومیت داشته باشد.ما با تعیین ضرایب بگونه ای عمل می کنیم تا فرم کلی شرایط مرزی تبدیل به شرایط مرزی مثال شود.به شرایط ابتدایی دقت کنید.مقدار q برابر 0 است تا b حذف شود.در متیجه p برابر با u می شود.و برای شرایط انتهایی نیز به همین صورت, q برابر صفر و مقدار p برابر با u-1 است.حالا نتایج رو در فایل bc1 ذخیره می کنیم.

function [pl,ql,pr,qr] = bc1(xl,ul,xr,ur,t)%BC1: MATLAB function M-file that specifies boundary conditions%for a PDE in time and one space dimension.pl = ul;ql = 0;pr = ur-1;qr = 0;

و همینطور شرط اولیه را در initial1.m ذخیره می کنیم.

function value = initial1(x)%INITIAL1: MATLAB function M-le that species the initial condition%for a PDE in time and one space dimension.value = 2*x/(1+x^2);

و حالا نوبت به حل مساله به کمک دستور pdepe رسیده است.مساله را در زمان 10ثانیه نخست و طول واحد(مثلا یک لوله به طول واحد) حل می کنیم.

%PDE1: MATLAB script M-file that solves and plots%solutions to the PDE stored in eqn1.mm = 0;% NOTE: m=0 specifies no symmetry in the problem. Taking% m=1 specifies cylindrical symmetry, while m=2 specifies% spherical symmetry.%% Define the solution meshx = linspace(0,1,20);t = linspace(0,10,10);%Solve the PDEu = pdepe(m,@eqn1,@initial1,@bc1,x,t);% Plot solutionfigure(1)surf(x,t,u);title('Surface plot of solution');xlabel('Distance x');ylabel('Time t');figure(2)for i=1:length(t) plot(x,u(i,:)) hold onend

جواب u بصورت یک ماتریس به اندازه t و x ذخیره شده است.برای مثال (u(1,5 مقدار دما در نقطه((t(1),x(5)مشخص می کند.ما می تونیم به کمک دستور((:,plot(x,u(1 بردار دما را در اغاز (t=0) رسم می کنیم.

:Example
$gif.latex?\pi^2u_{t}=u_{xx}$
$gif.latex?\dpi{100}%20u(t,0)=0$ $gif.latex?\dpi{100}%20\pi%20e^{-t}+u_{x}$
$gif.latex?\dpi{100}%20u(0,x)=sin\pi%20x$
وکد زیر رو برای مساله به این صورت می نویسیم:

function [c,f,s] = eqn2(x,t,u,DuDx)c = pi^2;f = DuDx;s = 0;

function [pl,ql,pr,qr] = bc2(xl,ul,xr,ur,t)pl = ul;ql = 0;pr = pi * exp(-t);qr = 1;

function u0 = initial2(x)u0 = sin(pi*x);

و از دستور pdepe استفاده می کنیم:

m = 0;x = linspace(0,1,20);t = linspace(0,5,20);u = pdepe(m,@eqn3,@initial3,@bc3,x,t);figure(1)surf(x,t,u);title('Surface plot of solution');xlabel('Distance x');ylabel('Time t');figure(2)plot(x,u(2,:))title('Solution at t = 2')xlabel('Distance x')ylabel('u(x,2)')% Creat animationfigure(3)fig = plot(x,u(1,:),'erase','xor');for k=1:length(t) set(fig,'xdata',x,'ydata',u(k,:),'color','r') pause(0.1)end

شکل شماره 3 یک انیمیشن خواهد بود که از زمان نخست تا حال پایدار را نمایش می دهد.

Example: $gif.latex?u_{t}=u_{xx}$
$gif.latex?\dpi{100}%20u_{x}(t,0)=0$ $gif.latex?\dpi{100}%20u_{x}(t,1)=0$
$2\leq%20x\leq%201\end{matrix}\right.$
:و کد زیر رو برای مساله به این صورت می نویسیم

function [c,b,s] = eqn3(x,t,u,DuDx)c = 1;b = DuDx;s = 0;

function [pl,ql,pr,qr] = bc2(xl,ul,xr,ur,t)pl = 0;ql = 1;pr = 0;qr = 1;

function value = initial2(x)if x<=0.5 value=x;else value=1-x;end

m = 0;x = linspace(0,1,20);t = linspace(0,0.2,20);u = pdepe(m,@eqn2,@initial2,@bc2,x,t);figure(1)surf(x,t,u);title('Surface plot of solution');xlabel('Distance x');ylabel('Time t');zlabel('Temperature u')

امید وارم از این پست استفاده کرده باشین.حتما این مثالها رو یکبار خودتون انجام بدین تا با مقدار دهی متغیرها در شرایط مرزی و معادله اصلی و شرط اولیه اشنا بشین.نظرهم یادتون نره خوشحال می شم نظراتتون رو بدونم.

اموزش متلب_pdepe(حل عددی معادله حرارت پاره ای وابسته به زمان)

مطالب مشابه :

معادله گرما

اموزش متلب_pdepe(حل عددی معادله حرارت پاره ای وابسته به زمان)

الگوریتم حل معادله گرما

الگوریتم حل معادلات گرما و موج

شیمی و مکانیک

انتقال گرما

حل معادله گرما يک بعدي غير دائم با روش ضمني کرانک نيکلسون

حل معادله حرارت با نرم افزار متلب (matlab)

گزارش کار انتقال حرارت