قضیه رمزی(ramsey)

این مساله در باره رنگ آمیزی گراف هاست که در اینجا به حالت خاصی از آن اشاره میکنیم. برای اعداد صحیح و دلخواه k و l کوچک ترین عدد صحیح (r(k,l وجود دارد به طوری که هر گراف با این تعداد راس دارای خوشه‌ای k راسی و یا شامل مجموعه مستقل l راسی است.

مثال

برای مثال

(r(x,۲)=x r(۱,x)=۱ ۱=r(x,۱

r(۴٬۵)=۲۵ r(۵٬۳)=۱۴ r(۴٬۴)=۱۸ r(۳٬۴)=۹ r(۳٬۳)=۶ عدد رمزی آخر در سال ۱۹۹۳ با استفاده از کامپیوتر بدست آمده.

تاریخچه

این اعداد را برای اولین بار رمزی نام گذاری کرد وبعد‌ها دانشمندان بزرگی چون گلیسون و گرینوودو اردوش بر روی آن‌ها وقضایای مربوطه کار کرده‌اند این اعداد فعلا تجربی اند و جز در موارد خواص فرمولی برای آن‌ها نداریم. برای آشنایی بیشتر به قضیه زیر توجه کنید.

قضیه کران بالا

در این جا میخواهیم کران بالایی برای اعداد رمزی (r(k,l بیان کنیم: اگر k>۱ , l>۱ آنگاه:

(r(k,l) >= r(k,l-۱) + r(k-۱,l

برهان:

فرض کنید g گرافی با (r(k,l-۱) + r(k-۱,l راس باشد. راس v را در نظر بگیرید صبق اصل لانه کبوتری v یا به (r(k-۱,l راس وصل است ویا به (r(k,l-۱ راس وصل نیست.

در صورتی که حالت اول بر قرار شود در این تعداد راس یا l راس مستقل اند ویا ۱-k راس خوشه‌اند واز آنجا که همه این رئوس به v وصل اند k-۱ راس به همراه k , v راس خوشه را تشکیل می‌دهند حکم مساله ثابت می‌شود.

و اگر حالت دوم بر قرار شود یا k راس خوشه پیدا می‌شود و یا l-۱ راس مستقل. واز آنجا که v به این رئوس وصا نیست l-۱ راس و l,v راس مستقل را تشکیل می‌دهد. و حکم ثابت می‌شود.

بیان مساله به صورت دیگر(حالت کلی):

اگر q1,q2,...,qn اعداد صحیح بزرگتر از 2 باشند آنگاه عددی مانند (r(q1,q2,...,qn وجود دارد به طوری که اگر p بزرگتر از (r(q1,q2,...,qn باشد و یال های گراف را با n رنگ (رنگ های 1 تا n) رنگ کنیم ,به ازای حداقل یک رنگ مانند i زیر گراف کامل qi راسی وجود دارد که یال هایش هم رنگ رنگ i ام است.

برای مثال r(3,3,3) = 17

حدس اردوس-فابر-لوواز (به انگلیسی: Erdős–Faber–Lovász conjecture) یک مسئله بسیار عمیق و مهم در بحث رنگ آمیزی گراف‌ها در نظریه گراف‌ها است.

این نظریه بیان می‌کند که: اجتماع k کپی از k دسته که هر ۲ دستهٔ متمایز دلخواه حداکثر در یک راس اشتراک دارند دارای عدد رنگی k است. حداد و تاردیف در سال ۲۰۰۴ این نظریه را به بیان دیگری و با مطرح کردن یک مثال از کمیته‌های موجود در دانشگاه ارایه کردند : فرض کنید در یک دانشکدهٔ دانشگاه k کمیـته وجود دارد و هر کـدام هم شامـل k نفر از اعضای هیئت علمی هستند و قرار است که همهٔ کمیته‌ها در یک اتاق با هم جلسه داشته باشند که در اتــاق k صندلی وجود دارد. همچنین فرض کنید که اشــتراک هر ۲ کمــیتهٔ متمایز دلخواه شامل ۱ نفر می‌شود. آیا ممکن است که اعضای کمیته‌ها را به صندلی‌هایی نسبت دهیم به طوری که هـر عضو در همه کمیته‌هایی که عضو آنها است روی صندلی ثابتی بنشیند؟ پاول اردوس ابتداً مبلغ ۵۰ دلار (دلار آمریکا) برای اثبات این حدس به عنوان جایزه قرار داده بود ولی بعداً آنرا به مبلغ ۵۰۰ دلار افزایش داد. بهترین نتیجهٔ یافته شده تا به امروز ایناست که عدد رنگی این مسئله حداکثر k + o(k) است. اگر مسئله را راحتتر و با شرایط کمتری در نظر بگیریم، بدین صورت که اجازه ئهیم دسته‌ها در هر چند راسی که می‌خواهند، اشتراک داشته باشند؛ آنگاه عدد رنگی این نوع گرافها حداکثر 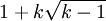$1 + k \sqrt{k - 1}$ خواهد شد.

قضیه رمزی(ramsey)

مثال

تاریخچه

قضیه کران بالا

بیان مساله به صورت دیگر(حالت کلی):

مطالب مشابه :

اعداد رمزی

فعالیت تکمیلی برای شناخت اعداد و رنگ ها

قضیه رمزی(ramsey)

آموزش جمع اعداد با حاصل دو رقمی

فعالیت تکمیلی برای شناخت اعداد و رنگ ها

آموزش ساخت برنامه رنگ آمیزی نقاشی با آدوب فلش ( یه شروع کلیدی )

رنگ‌آمیزی گراف

جمع اعداد یک رقمی با حاصل دو رقم در پایه ی اول