لگاریتم (2)
پیشینه
پیشینیان
ویراسنا، ریاضیدان هندی از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.]مایکل استیفل در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود.
از نپر تا اویلر

 جان نپر (۱۶۱۷-۱۵۵۰) بدست آورندهٔ روش لگاریتمگیری
جان نپر (۱۶۱۷-۱۵۵۰) بدست آورندهٔ روش لگاریتمگیری
روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.همچنین ژو بورجی (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد.
نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت 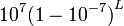 را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریبا برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریبا برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند:
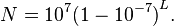
نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد:
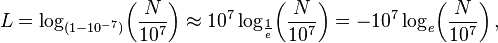
با تقریب خوبی داریم:
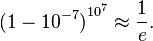
این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون بوناونتورا کاوالیری (Bonaventura Cavalieri) از ایتالیا، ادموند ونگت (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد.

 هذلولی y = ۱/x (منحنی قرمز) و سطح زیر آن از x = ۱ تا ۶ (قسمت نارنجی رنگ).
هذلولی y = ۱/x (منحنی قرمز) و سطح زیر آن از x = ۱ تا ۶ (قسمت نارنجی رنگ).
در سال ۱۶۴۷ گرگوآر دو سن-ونسان توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح 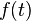 زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند:
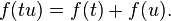
لگاریتم طبیعی اولین بار از سوی نیکولاس مرکاتور در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد. البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود. در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی و لگاریتم طبیعی را به گونهٔ زیر تعریف کرد:
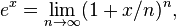
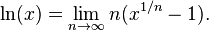
همچنین اویلر نشان داد که این دو تابع وارون یکدیگرند.
جدول لگاریتم، خطکش لغزان و کاربردها در گذشته

 متن سال ۱۷۹۷ دانشنامهٔ بریتانیکا در بارهٔ لگاریتم.
متن سال ۱۷۹۷ دانشنامهٔ بریتانیکا در بارهٔ لگاریتم.
با ساده سازی محاسبات پیچیده، از لگاریتم میتوان در دانش پیشرفته مانند اخترشناسی، نقشه برداری، هوانوردی و ... کمک گرفت. پیر سیمون لاپلاس دربارهٔ لگاریتم گفتهاست:
| « | وسیلهای ستودنی است که به کمک آن کار چند ماه به چند روز کاهش مییابد، عمر اخترشناسان را دو برابر میکند و از خطاهای کوچک میگذرد و از جملههای طولانی و جدانشدنی ریاضی بیزار است. | » |
وسیلهٔ کلیدی که پیش از در دسترس قرار گرفتن ماشین حساب و رایانه برای
محاسبهٔ لگاریتم از آن استفاده میشد و بوسیلهٔ آن بود که ارزش لگاریتم
روشن شد، جدول لگاریتم بود.چنین جدولی برای اولین بار بوسیلهٔ هنری بریگز در سال ۱۶۱۷ بلافاصله پس از ابتکار نپر ایجاد شد. پس از آن جدولهای وسیع تر و دقیق تری نوشته شد. در این جدولها مقدار 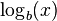 و
و 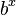 برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولا
پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی
اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که
تابع
برای هر عدد x در یک بازهٔ مشخص با دقت مشخص و برای پایههای مشخص (معمولا
پایهٔ ۱۰) نوشته شده بود. برای نمونه در اولین جدول بریگز، لگاریتم طبیعی
اعداد صحیح میان ۱ تا ۱۰۰۰ با دقت ۸ رقم اعشار نوشته شده بود. از آنجایی که
تابع 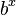 وارون
وارون 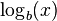 است به آن پادلگاریتم (به انگلیسی: antilogarithm) میگویند،لگاریتم ضرب و تقسیم دو عدد را همیشه به صورت جمع و تفاضل لگاریتمهای
آنها نشان میدادند. ضرب و تقسیم عبارت داخل لگاریتم را میتوان بوسیلهٔ
تابع پادلگاریتم و یا خود جدول بدست آورد:
است به آن پادلگاریتم (به انگلیسی: antilogarithm) میگویند،لگاریتم ضرب و تقسیم دو عدد را همیشه به صورت جمع و تفاضل لگاریتمهای
آنها نشان میدادند. ضرب و تقسیم عبارت داخل لگاریتم را میتوان بوسیلهٔ
تابع پادلگاریتم و یا خود جدول بدست آورد:
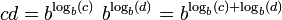
و
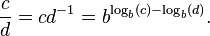
زمانی که رایانه در دسترس نیست، جستجوی جدولهای لگاریتم و استفاده از جمع و تفریق لگاریتمها بسیار آسان تر از روشهای ساده سازی مانند روش Prosthaphaeresis است. روش یاد شده بر پایهٔ اتحادهای مثلثاتی است. شمارش توانها و ریشههای اعداد به انجام عمل ضرب و تقسیم و جستجوی جدول به ترتیب زیر کاهش یافتهاست:
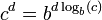
و
![\sqrt[d]{c} = c^{\frac 1 d} = b^{\frac{1}{d} \log_b (c)}. \,](http://www.bargozideha.com/static/portal/93/938153-322840.png)
در بسیاری از جدولها برای محاسبهٔ لگاریتم بخش اعشاری و بخش صحیح را از یکدیگر جدا میکردند مانند نمونهٔ زیر:
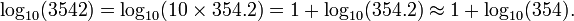
وسیلهٔ دیگری که برای شمارش لگاریتم کاربرد داشت، خطکش لغزان بود.
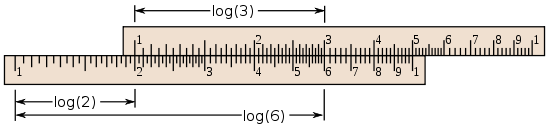
 شکل عمومی خطکش لغزان، در لبهٔ پایینی به لگاریتم ۲ میرسیم و با اضافه
کردن فاصله از لبهٔ بالایی، لگاریتم ۳ به حاصل ضرب یعنی لگاریتم ۶ میرسیم.
این خطکشها چنان درجه بندی شدهاند که گویی فاصلهٔ ۱ تا x ضریبی از لگاریتم x
است. برای نمونه برای لگاریتم ۶، فاصله از لگاریتم ۱ (یعنی صفر) تا ۲ روی
لبهٔ پایینی با فاصله از لگاریتم ۱ تا ۳ روی لبهٔ بالایی با هم جمع شد تا
فاصله از لگاریتم ۱ تا ۶ را نتیجه دهد.
شکل عمومی خطکش لغزان، در لبهٔ پایینی به لگاریتم ۲ میرسیم و با اضافه
کردن فاصله از لبهٔ بالایی، لگاریتم ۳ به حاصل ضرب یعنی لگاریتم ۶ میرسیم.
این خطکشها چنان درجه بندی شدهاند که گویی فاصلهٔ ۱ تا x ضریبی از لگاریتم x
است. برای نمونه برای لگاریتم ۶، فاصله از لگاریتم ۱ (یعنی صفر) تا ۲ روی
لبهٔ پایینی با فاصله از لگاریتم ۱ تا ۳ روی لبهٔ بالایی با هم جمع شد تا
فاصله از لگاریتم ۱ تا ۶ را نتیجه دهد.
مدت کوتاهی پس از کشف لگاریتم از سوی نپر، ادموند گونتر خطکشی (معیاری) برای بدست آوردن لگاریتم ایجاد کرد که لغزان نبود و به کمک آن میشد لگاریتمها را بدست آورد. پس از او ویلیام اوترد روش پیشرفتهتری را پیشنهاد کرد که دارای یک جفت لگاریتمهایی بود که در دو لبهٔ خطکش قرار داده شده بود و با لغزاندن دو لبهٔ خط کش میشد لگاریتم مورد نظر را به دست آورد. تا سال ۱۹۷۰ این خطکش وسیلهٔ محاسبهگر مهمی برای مهندسان و دانشمندان بود؛ چون به کمک آن، با دقت کافی و بسیار سریع تر از جدولها، میشد لگاریتم عدد را به دست آورد.
ویژگیهای ریاضی
مطالعهٔ بیشتر در بحث لگاریتم نیازمند مطرح کردن مفهوم تابع است. یک تابع مانند یک قانون عمل میکند که اگر یک عدد ورودی داشته باشد، در مقابل یک خروجی تولید میکند. مانند تابع توان x ام عدد حقیقی b که به صورت زیر نوشته میشود:
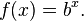
تابع لگاریتم
برای درک تابع لگاریتم باید نشان داد که معادلهٔ زیر:
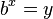
دارای راه حل و جواب یکتای x است به شرطی که y بزرگتر از صفر باشد و b بزرگتر از صفر و نامساوی ۱ باشد. برای اثبات این مطلب باید از قضیهٔ مقدار میانی در حساب دیفرانسیل و انتگرال استفاده کرد. این قضیه نشان میدهد که اگر تابع پیوستهای دو مقدار m و n
را تولید کند، هر مقداری میان این دو عدد را نیز به دلیل پیوستگی میتواند
تولید کند. یک تابع را زمانی پیوسته میدانیم که در هیچ نقطهای ار آن
«پرش» نداشته باشیم و بدون بلندکردن قلم از روی کاغذ بتوانیم خم آن را
بکشیم. میتوان نشان داد که در تابع 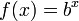 نیز همین ویژگی وجود دارد، برای هر y > ۰ که میان دو مقدار
نیز همین ویژگی وجود دارد، برای هر y > ۰ که میان دو مقدار 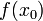 و
و 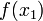 به ازای x۰ و x۱ قرار داشته باشد طبق قضیهٔ مقدار میانی میتوان یک x پیدا کرد که
به ازای x۰ و x۱ قرار داشته باشد طبق قضیهٔ مقدار میانی میتوان یک x پیدا کرد که 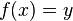 باشد. بنابراین برای معادلهٔ
باشد. بنابراین برای معادلهٔ 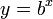 یک جواب پیدا شد که میتوان گفت تنها جواب این معادلهاست چون تابع f برای
b > ۱ اکیدا صعودی و برای b میان ۰ و ۱ اکیدا نزولی است.
یک جواب پیدا شد که میتوان گفت تنها جواب این معادلهاست چون تابع f برای
b > ۱ اکیدا صعودی و برای b میان ۰ و ۱ اکیدا نزولی است.
جواب پیدا شده برای این معادله همان لگاریتم y در پایهٔ b است.
تابع وارون
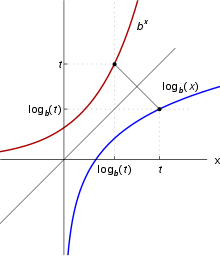
 خم تابع لگاریتم (آبی) و خم تابع توانی (قرمز)
خم تابع لگاریتم (آبی) و خم تابع توانی (قرمز)
لگاریتم تابع توانی برای هر عدد x به صورت زیر نوشته میشود:
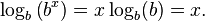
اگر پایهٔ توان و لگاریتم هر دو b باشد جواب نهایی رابطهٔ بالا قطعا خود x خواهد بود. همچنین اگر عدد مثبت y را داشته باشیم، رابطهٔ زیر نیز برقرار خواهد بود:
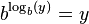
بنابراین در هر دو صورت میتوان دو تابع توانی و لگاریتم را ترکیب کرد و دوباره به مقدار اولیه رسید. پس لگاریتم در پایهٔ b تابع وارون f(x) = bx است.[۲۹]
دو تابع وارون همواره با یکدیگر ارتباط دارند به این ترتیب که خمهای
آنها قرینهٔ یکدیگر نسبت به خط y = x است (مانند شکل) همچنین در تابع 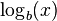 اگر x به سمت مثبت بی نهایت برود مقدار تابع لگاریتم نیز به ازای b > ۱ به سمت مثبت بی نهایت خواهد رفت در این حال میگوییم تابع
اگر x به سمت مثبت بی نهایت برود مقدار تابع لگاریتم نیز به ازای b > ۱ به سمت مثبت بی نهایت خواهد رفت در این حال میگوییم تابع 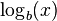 اکیدا صعودی است. به ازای b < ۱ اگر x به سمت مثبت بی نهایت رود، مقدار تابع
اکیدا صعودی است. به ازای b < ۱ اگر x به سمت مثبت بی نهایت رود، مقدار تابع 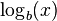 به سمت منفی بی نهایت میرود. وقتی x به سمت صفر میرود مقدار تابع
به سمت منفی بی نهایت میرود. وقتی x به سمت صفر میرود مقدار تابع 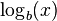 برای b > ۱ به سمت منفی بی نهایت میرود و برای b < ۱ به سمت مثبت بی نهایت میرود.
برای b > ۱ به سمت منفی بی نهایت میرود و برای b < ۱ به سمت مثبت بی نهایت میرود.
مشتق و پادمشتق
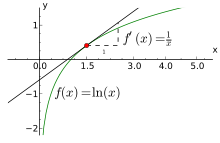
 خم تابع لگاریتم طبیعی (سبز) و خط مماس با آن در نقطهٔ x = ۱٫۵ (سیاه)
خم تابع لگاریتم طبیعی (سبز) و خط مماس با آن در نقطهٔ x = ۱٫۵ (سیاه)
ویژگیهای ریاضی یک تابع را میتوان در تابع وارون آن نیز جستجو کرد. پس چون f(x) = bx یک تابع پیوسته و مشتقپذیر است، میتوان نتیجه گرفت که 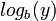 نیز همین ویژگی را دارد. یک تابع پیوسته مشتقپذیر است اگر هیچ نقطهٔ تیزی
(نقطهٔ شکستگی) در آن وجود نداشته باشد. از آنجایی که میتوان نشان داد که
مشتق
نیز همین ویژگی را دارد. یک تابع پیوسته مشتقپذیر است اگر هیچ نقطهٔ تیزی
(نقطهٔ شکستگی) در آن وجود نداشته باشد. از آنجایی که میتوان نشان داد که
مشتق 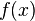 برابر با
برابر با 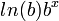 است، با استفاده از ویژگیهای تابع نمایی و قاعدهٔ زنجیری به این نتیجه میرسیم که مشتق
است، با استفاده از ویژگیهای تابع نمایی و قاعدهٔ زنجیری به این نتیجه میرسیم که مشتق 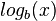 برابر است با:
برابر است با:
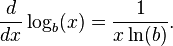
که این شیب خط مماس در نقطهٔ x بر خم 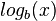 است که برابر است با
است که برابر است با 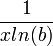 . همچنین مشتق
. همچنین مشتق 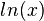 برابر با
برابر با  است که به این معنی است که پادمشتق
است که به این معنی است که پادمشتق  همان
همان 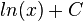 است. اگر بجای x حالت کلی
است. اگر بجای x حالت کلی 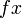 را در نظر بگیریم، در این حالت خواهیم داشت:
را در نظر بگیریم، در این حالت خواهیم داشت:
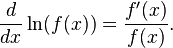
گاهی برای بدست آوردن مشتق تابع f از 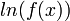 استفاده میکنند که به این کار مشتقگیری لگاریتمی میگویند. پادمشتق لگاریتم طبیعی
استفاده میکنند که به این کار مشتقگیری لگاریتمی میگویند. پادمشتق لگاریتم طبیعی 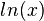 برابر است با:
برابر است با:
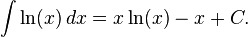
رابطههای مرتبط با دیگر پایههای لگاریتم با استفاده از فرمول لگاریتم طبیعی که در بالا گفته شد بدست میآید.
بیان انتگرالی لگاریتم طبیعی
لگاریتم طبیعی t برابر است با انتگرال 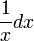 از ۱ تا t:
از ۱ تا t:
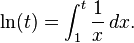
به عبارت دیگر 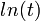 برابر است با سطح میان محور xها و نمودار تابع
برابر است با سطح میان محور xها و نمودار تابع  از 1 = x تا
از 1 = x تا 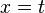 (شکل مقابل). این مطلب، از نتایج قضیهٔ اساسی حسابان و اینکه مشتق
(شکل مقابل). این مطلب، از نتایج قضیهٔ اساسی حسابان و اینکه مشتق 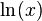 ،
،  است، میباشد. عبارت سمت راست این رابطه را میتوان به عنوان تعریفی برای لگاریتم طبیعی در نظر گرفت. فرمولهای ضرب و توان لگاریتمی را میتوان از این تعریف نتیجه گرفت. برای نمونه
است، میباشد. عبارت سمت راست این رابطه را میتوان به عنوان تعریفی برای لگاریتم طبیعی در نظر گرفت. فرمولهای ضرب و توان لگاریتمی را میتوان از این تعریف نتیجه گرفت. برای نمونه 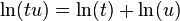 را میتوان به صورت زیر نتیجه گرفت:
را میتوان به صورت زیر نتیجه گرفت:
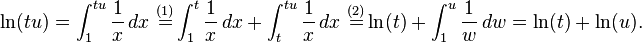
بخش نخست تساوی انتگرال را به دو بخش جدا میشکند و بخش دوم تساوی، تغییر متغیر میدهد (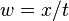 ).
در نگارهای که در پایین نشان داده شدهاست، سطح زیر منحنی که برابر با
انتگرال بالا است به دو ناحیهٔ آبی و زرد تقسیم شدهاست. در قسمت آبی همان
طور که خم در جهت x کشیده شده (t برابر شده) به همان اندازه هم در جهت عمودی دچار جمعشدگی شدهاست بنابراین سطح زیر منحنی سمت راست که انتگرال f(x) = 1/x از 1 تا u است با سطح زیر آن از t تا tu برابر است. پس روی شکل سمت چپ نشان داده شد که
).
در نگارهای که در پایین نشان داده شدهاست، سطح زیر منحنی که برابر با
انتگرال بالا است به دو ناحیهٔ آبی و زرد تقسیم شدهاست. در قسمت آبی همان
طور که خم در جهت x کشیده شده (t برابر شده) به همان اندازه هم در جهت عمودی دچار جمعشدگی شدهاست بنابراین سطح زیر منحنی سمت راست که انتگرال f(x) = 1/x از 1 تا u است با سطح زیر آن از t تا tu برابر است. پس روی شکل سمت چپ نشان داده شد که 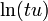 یا سطح زیر منحنی برابر است با مجموع
یا سطح زیر منحنی برابر است با مجموع 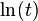 و
و 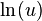 (سطح زرد و آبی)
(سطح زرد و آبی)

 اثبات نموداری رابطهٔ ضرب در لگاریتم طبیعی.
اثبات نموداری رابطهٔ ضرب در لگاریتم طبیعی.
رابطهٔ توان 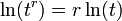 را نیز به همین ترتیب میتوان اثبات کرد:
را نیز به همین ترتیب میتوان اثبات کرد:
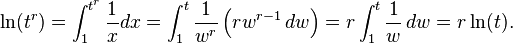
در تساوی دوم تغییر متغیر 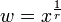 را داریم.
را داریم.
مجموع وارونهای اعداد طبیعی:
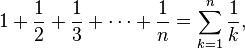
که سری هارمونی نام دارد، به لگاریتم طبیعی بسیار نزدیک است: هرگاه n به سمت بینهایت برود، تفاضل زیر:
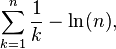
به عددی معروف به ثابت اویلر-مسکرونی، همگرا میشود. این ارتباط در تحلیل عملکرد الگوریتمهایی مانند مرتبسازی سریع کمک میکند.
محاسبه
در بعضی موارد مانند ۳ = (۱۰۰۰) log۱۰ محاسبهٔ لگاریتم بسیار آسان است. در حالت کلی لگاریتم را به کمک سریهای توانی یا ابزارهای محاسباتی-هندسی و یا به کمک بازیابی جدول لگاریتم که پیش از این محاسبه شده و دقت کافی دارد، محاسبه میکنند.[۳۷][۳۸] همچنین برای محاسبهٔ 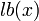 میتوان از الگوریتم لگاریتمهای دودویی که به صورت بازگشتی و بر پایهٔ مربعهای پشت هم از x عمل میکند استفاده کرد:
میتوان از الگوریتم لگاریتمهای دودویی که به صورت بازگشتی و بر پایهٔ مربعهای پشت هم از x عمل میکند استفاده کرد:
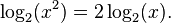
روش تقریبی نیوتن که یک روش تکرار شونده برای حل تقریبی معادلات است، میتواند برای بدست آوردن مقدار لگاریتم مفید باشد؛ چون تابع وارون لگاریتم، تابع نمایی با تقریب خوبی قابل محاسبهاست.[۳۹] در صورتی که تنها ابزار در دسترس ابزار جمع و اعداد پایهٔ دو باشد، میتوان با جستجو در میان جدول CORDIC یا «روش رقم به رقم» روشهای مناسبی برای محاسبهٔ لگاریتم پیدا کرد.
سریهای توانی
سری تیلور

 سری تیلور. این پویانمایی مقدار سری تیلور را به ازای ۱۰ جملهٔ اول سپس جملههای ۹۹ و ۱۰۰ نشان دادهاست.
سری تیلور. این پویانمایی مقدار سری تیلور را به ازای ۱۰ جملهٔ اول سپس جملههای ۹۹ و ۱۰۰ نشان دادهاست.
برای هر عدد حقیقی z که میان کوچکتر از 2 و بزرگتر از صفر است رابطهٔ زیر برقرار است:
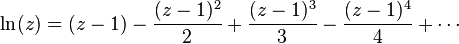
با استفاده از روابط زیر 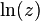 را میتوان دقیقتر بدست آورد:
را میتوان دقیقتر بدست آورد:

برای نمونه، تقریب سوم به ازای z = ۱٫۵ نتیجه برابر با ۰٫۴۱۶۷ خواهد بود که تقریبا ۰٫۱۱ بیشتر از ۰٫۴۰۵۴۶۵ = (۱٫۵) ln است. در حساب دیفرانسیل غیر پیشرفته، 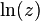 را به عنوان حد این نوع سریها در نظر میگیرند. که به آن بسط تیلور لگاریتم طبیعی به ازای z = ۱ میگویند.
را به عنوان حد این نوع سریها در نظر میگیرند. که به آن بسط تیلور لگاریتم طبیعی به ازای z = ۱ میگویند.
دیگر سریهای پرکاربرد
سری دیگر برپایهٔ تابع وارون تانژانت هذلولوی (وارون تانژانت هیپربولیک) است، این سری برای اعداد مختلط z با بخش حقیقی[۴۲] مثبت است که به صورت زیر نوشته میشود:
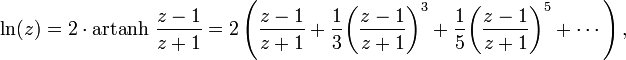
با استفاده از مفهوم جمع (سیگما) میتوان این سری را به گونهٔ دیگری نوشت:
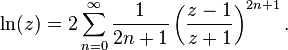
این سری از سری تیلور که در بالا گفته شد گرفته میشود ولی خیلی زودتر از تیلور همگرا میشود.بویژه زمانی که z عددی نزدیک ۱ باشد. برای نمونه برای z = ۱٫۵ سه جملهٔ اول سری دوم با خطایی برابر با ۶-۱۰ × ۳ تقریبا میتوان گفت تقریبا برابر با (۱٫۵)ln است. اینکه به ازای zهای نزدیک به ۱ سری زودتر همگرا میشود را میتوان به کمک رابطهٔ زیر نشان داد:
فرض کنید تقریبا 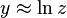 و رابطهٔ زیر را نیز داریم:
و رابطهٔ زیر را نیز داریم:
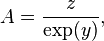
میتوان از دو سوی رابطهٔ بالا لگاریتم گرفت:
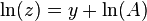
هرچه مقدار لگاریتم z دقیقتر باشد باید 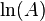 به صفر نزدیک تر باشد درنتیجه A به ۱ نزدیکتر است. مقدار A به کمک سریهای نمایی محاسبه میشود که این سریها، اگر y بزرگ نباشد، خیلی زود همگرا میگردند.
به صفر نزدیک تر باشد درنتیجه A به ۱ نزدیکتر است. مقدار A به کمک سریهای نمایی محاسبه میشود که این سریها، اگر y بزرگ نباشد، خیلی زود همگرا میگردند.
برای آسان تر کردن محاسبهٔ 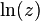 میتوان آن را به مقدارهای کوچکتر خُرد کرد به این ترتیب که بگوییم a × ۱۰b = z و لگاریتم آن را به صورت
میتوان آن را به مقدارهای کوچکتر خُرد کرد به این ترتیب که بگوییم a × ۱۰b = z و لگاریتم آن را به صورت 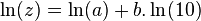 بنویسیم.
بنویسیم.
از روش مشابهی میتوان استفاده کرد تا به کمک آن لگاریتم اعداد صحیح را بدست آورد:
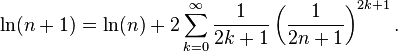
اگر لگاریتم عدد بزرگ n معلوم باشد، میتوان لگاریتم n + ۱ را با همگرایی سریع سری بالا بدست آورد.
میانگین حسابی-هندسی [ویرایش]
با کمک میانگین حسابی-هندسی میتوان با دقت خوبی لگاریتم طبیعی عددی مانند x را بدست آورد. میزان تقریب آن برابر با 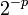 است. این رابطه از سوی ریاضیدان آلمانی کارل فریدریش گاوس پیشنهاد شد.[۴۳][۴۴]
است. این رابطه از سوی ریاضیدان آلمانی کارل فریدریش گاوس پیشنهاد شد.[۴۳][۴۴]
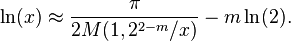
در اینجا M نماد میانگین حسابی-هندسی است که از تکرار محاسبهٔ میانگین حسابی و ریشهٔ دوم ضرب دو عدد (میانگین هندسی) بدست میآید. همچنین m از راه انتخابی مانند زیر بدست میآید:
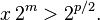
مطالب مشابه :
لگاریتم (2)
روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio
لگاریتم
برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را
لگاريتم
لگاریتم: یک عدد در یک پایه، توانی از پایه است که برابر آن عدد است. تابع لُگاريتم معکوس تابع
لگاریتم (1)
لُگاریتم یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه
تابع لگاریتمی
توابع لگاریتم در پایه می دانیم که اگر عدد مثبتی به جز یک باشد، تابع مشتق پذیر و یک به یک است.
لگاریتم
پگاه ریاضی - لگاریتم - لذت ریاضی را با مهران تجربه کنید
برچسب :
لگاریتم
